A Funcţie la matematică este o relație specială între setul de valori de intrare și setul de valori de ieșire. În Funcție, fiecare valoare de intrare oferă o anumită valoare de ieșire. Reprezentăm o funcție în matematică ca, y = f(x) unde X este valoarea de intrare și pentru fiecare X obținem o valoare de ieșire ca y.

În acest articol, vom afla despre, funcții în matematică, diferitele lor tipuri, exemple și altele în detaliu.

Cuprins

• Ce este o funcție în matematică?
• Definiția funcției în matematică
• Exemple de funcții
• Condiție pentru o funcție
• Reprezentarea funcțiilor în matematică
• Identificarea funcției
• Tipuri de funcții
• Ce este o funcție în algebră?
• Domeniul și domeniul unei funcții
• Compoziția funcțiilor
• Algebra funcțiilor
• Ce este o funcție pe un grafic?
• Funcții de reprezentare grafică
• Funcții comune
• Aplicații ale funcțiilor
• Exemple despre funcție
• Exersați probleme despre ce este o funcție

Ce este o funcție în matematică?

O funcție în matematică este a relație între valorile de intrare (domeniu) și valorile de ieșire (domeniu) ale seturilor date, astfel încât două variabile din seturile de domenii să nu fie legate de aceeași variabilă din setul de intervale. Un exemplu simplu de funcție în matematică este f(x) = 2x, care este definit pe R→R, aici orice variabilă din domeniu este legată de o singură variabilă din interval.

O funcție din matematică are un domeniu, un codomeniu și un domeniu. Domeniul este mulțimea tuturor valorilor posibile ale lui x și domeniul funcției este mulțimea tuturor valorilor de ieșire ale lui y. Intervalul este submulțimea codomeniului unei funcții. De asemenea, putem spune că o funcție în matematică este o relație cu o ieșire unică și nicio valoare de intrare nu are o ieșire similară într-o funcție, ceea ce este cazul relației.

Definiția funcției în matematică

Funcția este o relație specială sau o metodă care conectează fiecare membru al mulțimii A la un membru unic al mulțimii B printr-o relație definită. Setul A se numește domeniul și setul B se numește co-domeniul funcției. O funcție în matematică de la mulțimea A la mulțimea B este definită ca:

f = ∀ a ∈ A, b ∈ B

Fiecare funcție este o relație, dar fiecare relație nu este o funcție. Criteriile pentru ca orice relație să fie considerată o funcție, deoarece în funcție fiecare element al mulțimii A are o singură imagine în mulțimea B, în timp ce în relație un element al mulțimii A poate avea mai multe imagini în mulțimea B.

Definim o funcție în matematică de la mulțimea nevide A la mulțimea nevidă B astfel încât,

(a, b) ∈ f, atunci f(a) = b

unde am sunat b ca imagine a A definit în cadrul relaţiei f .

Fiecare element 'A' al setului A are o imagine unică „ b „în setul B atunci este o funcție.

Funcții Exemple

O funcție în matematică f este definită ca, y = f(x) unde X este valoarea de intrare și pentru fiecare valoare de intrare a lui x, obținem o valoare unică a lui y. Diverse exemple de funcții în matematică definite pe R→R sunt:

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 etc

Condiție pentru o funcție

Pentru oricare două seturi nevide A și B, o funcție f: A→B denotă că f este o funcție de la A la B, unde A este un domeniu si B este un co-domeniu.

Pentru orice element, a ∈ A, un element unic, b ∈ B este astfel încât (a,b) ∈ f. Elementul unic b care este înrudit cu a este notat cu f(a) și se citește ca f din a. Acest lucru poate fi înțeles mai bine din imaginea de mai jos:

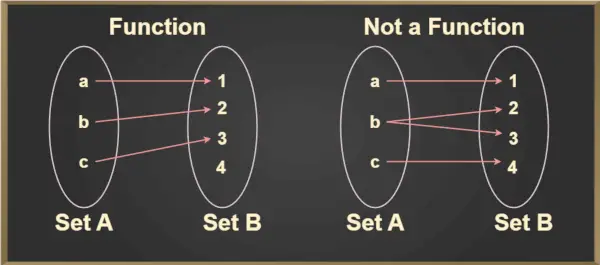
Test de linie verticală

Testul de linie verticală este utilizat pentru a determina dacă o curbă este o funcție sau nu. Dacă orice curbă taie o linie verticală în mai mult de un punct, atunci curba nu este o funcție.

Reprezentarea funcțiilor în matematică

Reprezentăm o funcție în matematică ca,

y = f(x) = x + 3

Aici, setul de valori ale lui x este domeniul funcției, iar setul de valori de ieșire a lui y este co-domeniul funcției. Aici, funcția este definită pentru toate numerele reale, deoarece oferă o valoare unică pentru fiecare x, dar nu este întotdeauna posibil să obținem rezultatul pentru fiecare valoare a lui x, în acest caz definim funcția în două părți, aceasta poate fi înțeleasă ca

• f(x) = 1/(x – 2), unde x ≠ 2
• f(x) = x²unde x ∈ {R}

Putem defini o funcție în matematică ca o mașină care preia o anumită intrare și oferă o ieșire unică. Funcția f(x) = x²este definit mai jos ca,

Putem reprezenta o funcție în matematică prin metoda celor trei ca:

• Set de perechi comandate
• Formular de masă
• Forma grafică

De exemplu, dacă reprezentăm o funcție ca, f(x) = x³

Un alt mod de a reprezenta aceeași funcție este ca set de perechi ordonate la fel de,

f = {(1,1), (2,8), (3,27)}

În setul menționat mai sus, domeniul funcției este D = {1, 2, 3} și domeniul funcției este R = {1, 8, 27}

alfabet în numere

Identificarea funcției

Funcția este clasificată ca un tip special de relație în matematică. Există următoarele reguli care pot fi folosite pentru a identifica o funcție:

• O relație în care fiecare intrare mapată la o ieșire unică este o funcție. Aceasta a numit funcția unu la unu.
• O relație în care două intrări (preimagine) mapate la o singură ieșire este, de asemenea, o funcție. Aceasta este funcția de mai multe la una.
• O relație în care o intrare este mapată două ieșiri diferite nu este o funcție.
• O relație în care multe intrări sunt mapate la mai multe ieșiri urmând nicio regulă specifică nu este o funcție.

Tipuri de funcții

Diferit Tipuri de funcții sunt folosite pentru rezolvarea diferitelor tipuri de probleme matematice legate în special de curbe și ecuații. Există trei tipuri majore de funcții în matematică care se bazează pe maparea elementelor de la setul A la setul B.

Funcție injectivă sau Funcție unu la unu

Funcția în care fiecare element al domeniului are o imagine distinctă în codomeniu se numește Injectiv sau Funcția unu-la-unu .

f: A → B se spune că este unul la unu sau injectiv dacă imaginile elementelor distincte ale lui A sub f sunt distincte, adică

fa ₁ ) = b ₁ , f(a ₂ ) = b ₂

unde un₁, A₂∈ A și b₁, b₂∈ B

Funcții surjective sau Onto Function

Funcția surjectivă este funcția în care fiecare element al codomeniului are o pre-imagine în domeniu. Se mai numeste Pe Funcție ceea ce înseamnă că fiecare element al codomeniului este asociat cu fiecare element al domeniului. Niciun element al codomeniului nu ar trebui să aibă o relație goală. Numărul de elemente de codomeniu și interval este același.

f: A → B se spune că este pe, dacă fiecare element al lui B este imaginea unui element al lui A sub f, adică pentru fiecare b ϵ B, există un element „a” în A astfel încât f(a) = b.

Funcția bijectivă

Dacă o funcție are proprietăți atât Injective(One to One) cât și Surjective(Onto), atunci funcția se numește Funcția bijectivă . În Funcția Bijectivă, fiecare element al domeniului este legat de fiecare element al codomeniului și, de asemenea, există o relație unu-la-unu. Aceasta implică faptul că numărul de elemente ale codomeniului și al intervalului sunt același și niciun element din domeniu sau din codomeniu nu are relație goală.

Pe baza valorilor de ieșire, funcțiile sunt clasificate ca funcții pare și impare. Să aruncăm o privire asupra lor

Funcții ciudate

Funcția impară este un tip de funcție care prezintă simetrie față de origine. Mai exact, dacă f(x) este o funcție impară, ea arată că f(-x) = -f(x)

Funcție chiar

Funcția chiar este un tip de funcție care prezintă simetrie față de axa y. Mai exact, dacă f(x) este o funcție pară, ea arată că f(-x) = f(x)

Ce este o funcție în algebră?

O funcție în algebră este o ecuație pentru care orice x care poate fi introdus în ecuație va produce exact o ieșire, cum ar fi y din ecuație. Este reprezentată ca y = f(x), unde x este o variabilă independentă și y este o variabilă dependentă.

De exemplu:

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Domeniul și domeniul unei funcții

Domeniu și interval ale unei funcții sunt valoarea de intrare și respectiv de ieșire a unei funcții. De exemplu, să presupunem că avem o funcție dată ca f(x) = x². Aici, putem lua tot numărul real ca valoare de intrare a lui x și rezultatul va fi întotdeauna un număr real pozitiv. Prin urmare, domeniul său este un set de numere reale reprezentate ca R, în timp ce domeniul său este un set de numere reale pozitive reprezentate ca R⁺

Compoziția funcțiilor

Dacă f: A → B și g: B→ C sunt două funcții. Atunci compoziția lui f și g se notează cu f(g) și este definită ca funcție ceață = f(g(x)) pentru x ∈ A.

Să luăm două funcții f(x) = x + 3 și g(x) = 2x²

ceață = f(g(x))

⇒ ceață = f(2x²)

⇒ dinte = 2x²+ 3

Află mai multe, Compoziția funcției

Algebra funcțiilor

Algebra funcțiilor implică operațiile algebrice efectuate între două funcții. Operația algebrică pentru două funcții f(x) și g(x) definite pe valoarea reală a lui x sunt menționate mai jos:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Pentru că k este un număr real}
• (f/g)(x) = f(x) /g(x); {Pentru g(x) ≠ 0}

Ce este o funcție pe un grafic?

O funcție poate fi ușor reprezentată pe un grafic. Orice funcție din grafic reprezintă o curbă (inclusiv linia dreaptă) în planul x-y mapat pentru valorile sale de intrare și de ieșire corespunzătoare.

Pentru a reprezenta o funcție pe o primă, găsiți câteva puncte care se află pe funcție și apoi uniți aceste puncte conform locului funcției. De exemplu, pentru a reprezenta grafic funcția (linia dreaptă) f(x) = y = 5x – 2 avem nevoie de un punct de pe grafic. Pentru a găsi punctul de pe grafic, luăm mai întâi valorile aleatorii ale lui x și apoi găsim valorile corespunzătoare ale lui y, ca,

f(x) = y = 5x- 2

dacă x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

dacă x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

dacă x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Acum unind aceste puncte putem obține graficul funcției y = 5x – 2

Funcții de reprezentare grafică

Cunoașterea valorilor lui x permite reprezentarea unei funcții f(x) pe un grafic. Deoarece y = f(x), putem găsi valoarea asociată pentru y începând cu valorile lui x. Ca rezultat, putem reprezenta un grafic într-un plan de coordonate folosind valorile x și y. Luați în considerare următorul scenariu:

Presupunem y = x + 3

Când x = 0, y = 3

În mod similar,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Ca rezultat, putem reprezenta graficul pentru funcția x + 3 folosind aceste valori.

Funcții comune

Câteva funcții comune utilizate în mod obișnuit în matematică sunt discutate mai jos:

Funcție reală

Funcție reală în matematică se referă la o funcție al cărei domeniu și domeniu sunt submulțimi ale numerelor reale (notate ca ℝ). În termeni mai simpli, o funcție reală este o regulă sau o relație matematică care atribuie o valoare a unui număr real fiecărui număr real introdus.

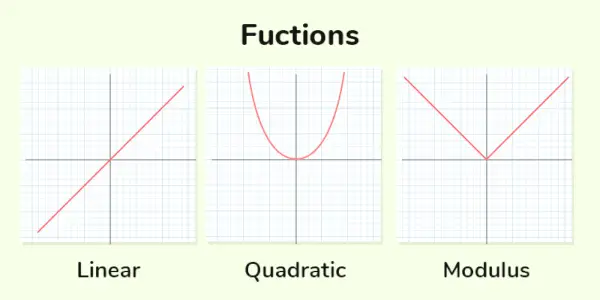
Funcții reale

Funcția polinomială

Funcția în care exponenții variabilelor algebrice sunt numere întregi nenegative se numește a Funcția polinomială . Dacă puterea variabilei este 1 se numește funcție liniară, dacă puterea este 2 se numește funcție pătratică, iar dacă puterea este 3 se numește funcție cubică. Câteva exemple de funcții polinomiale sunt menționate mai jos:

• y = x²
• y = 2x + 3
• y = 3x³

Funcția polinomială poate fi clasificată în următoarele tipuri:

Funcție liniară : Funcția liniară este acelea în care puterea maximă a variabilei este 1. Forma generală a Funcție liniară este y = mx + c

Funcția pătratică : Funcția cuadratică este cele în care puterea maximă a variabilei este 2. Forma generală a funcţie pătratică este, topor ² + bx + c = 0

Funcția cubică : Funcția cubică este cele în care puterea maximă a variabilei este 3. Forma generală a funcției cubice este dată ca topor ³ + bx ² + cx + d = 0

Funcție inversă

Funcție inversă este funcția care conține inversul unei alte funcții. Să presupunem că avem o funcție y = f(x), atunci funcția ei inversă va fi x = f^-1(y). În y = f(x), domeniul este x și intervalul este y, în timp ce în cazul lui x = f^-1(y), domeniul este y și intervalul este x. Astfel putem spune că domeniul funcției inițiale este domeniul funcției sale inverse și domeniul funcției originale este domeniul funcției originale. Câteva exemple de funcții inverse sunt:

• y = deci^-1(X)
• y = x^-1

Funcția de zonă

Funcția de zonă se referă de obicei la o funcție matematică care calculează aria unei forme geometrice sau a unei regiuni. Funcția de zonă preia unul sau mai mulți parametri ca intrare și returnează zona formei corespunzătoare. Unele dintre funcțiile zonei sunt discutate mai jos:

Funcția de zonă a cercului : Zona cercului (A) este o funcție a razei sale (r) astfel încât,

A = πr ²

Funcția aria triunghiului : Aria triunghiului (A) este o funcție a bazei (b) și a înălțimii (h) astfel încât,

A = (bh)/2

Functie exponentiala

Functie exponentiala este cea care este reprezentată ca f(x) = e^X. Este adesea folosit pentru a arăta o creștere sau degradare rapidă.

Funcția logaritmică

Funcția logaritmică este o funcție matematică care reprezintă operația inversă de exponențiere. Este reprezentat ca f(x) = log x.

Funcția de tavan

Funcția de tavan , notat cu ⌈x⌉, rotunjește un număr real x până la cel mai apropiat număr întreg care este mai mare sau egal cu x. Cu alte cuvinte, găsește cea mai mică valoare întreagă care este mai mare sau egală cu x.

Funcția de podea

Funcția etaj, notată ca ⌊x⌋, rotunjește un număr real x la cel mai apropiat număr întreg care este mai mic sau egal cu x. Cu alte cuvinte, găsește cea mai mare valoare întreagă care este mai mică sau egală cu x.

Funcția de modul

Funcția de modul , cunoscută și sub numele de funcție de valoare absolută, returnează mărimea sau dimensiunea unui număr real fără a ține cont de semnul acestuia. Funcția modul este notată ca ∣x∣, unde x este valoarea de intrare.

Funcția Signum

Funcția Signum , cunoscută și sub numele de funcție semn sau funcție signum, este o funcție matematică care returnează semnul unui număr real. Indică dacă numărul este pozitiv, negativ sau zero.

Funcții trigonometrice

Funcții trigonometrice sunt funcții matematice care raportează unghiurile unui triunghi dreptunghic de lungimile laturilor sale. Cele șase funcții trigonometrice primare sunt sinus (sin), cosinus (cos), tangentă (tan), cosecantă (cosec), secantă (sec) și cotangentă (cot).

Funcții complexe

Orice funcție în care variabilele de intrare sunt funcții complexe se numesc funcție complexă. Un număr complex este un număr care poate fi reprezentat pe plan complex. Într-o număr complex avem număr real și număr imaginar. Un număr complex (z) este reprezentat ca, z= x + iy și o funcție complexă este reprezentată ca, f(z) = P(x, y) + iQ(x, y)

Aplicații ale funcțiilor

Când spunem că o mărime variabilă y este o funcție a unei mărimi variabile x, indicăm că y este dependent de x și că valoarea lui y este determinată de valoarea lui x. Această dependență poate fi exprimată astfel: f = y (x).

• Raza unui cerc poate fi folosită pentru a calcula aria unui cerc. Raza r afectează zona A. Declarăm că A este o funcție a lui r în limbajul matematic al funcțiilor. Putem scrie A = f(r) =π×r²
• Volumul V al unei sfere este o funcție a razei acesteia. V = f(r) = 4/3×r³denotă dependența lui V de r.
• Forța este o funcție a accelerației unui corp de masă fixă ​​m. F = g(a) = m×a.

Oamenii citesc și:

• Relație și funcție
  
• Domeniul și gama de funcții trigonometrice
• Domeniul unei funcții
• Funcția hiperbolică

Exemple despre funcție

Exemplul 1: Pentru două funcții f și g sunt definite ca, f(x) = x ² și g(x) = ln(2x). Găsiți funcția compusă (gof )( x )

Soluţie:

Dat:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Astfel, (gof)(x) = 2 ln(√2x)

Exemplul 2: Găsiți rezultatul funcției g(t)= 6t ² + 5 la

• (i) t = 0
• (ii) t = 2

Soluţie:

Funcția dată,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Exemplul 3: Lungimea unui dreptunghi este de cinci ori lățimea sa, exprimă aria dreptunghiului în funcție de lungimea acestuia.

Soluţie:

Fie lungimea dreptunghiului l, iar lățimea dreptunghiului este b

Acum,

• b = l/5

Aria dreptunghiului (A) = l × l/5 = l²/5

Astfel, aria dreptunghiului ca funcție a lungimii acestuia este,

A(l) = l ² /5

Exersați probleme despre ce este o funcție

1. Având în vedere funcția f(x)=3x+5

• Găsiți f(2)
• Găsiți f(−1)
• Determinați domeniul și domeniul funcției.

2. Având în vedere funcția g(x)=x ² – 4x + 3

• Găsiți rădăcinile funcției.
• Găsiți g(3) și g(0).
• Determinați vârful funcției.

3. Având în vedere două funcții f(x)=x + 2 și h(x)=2x – 3

• Găsiți funcția compusă (f ∘ h) (x)
• Evaluați (f ∘ h)(2)

Rezumat – Ce este o funcție

O funcție în matematică este o relație specială între valorile de intrare (domeniu) și valorile de ieșire (domeniu) în care fiecare intrare este asociată cu o ieșire unică. Reprezentate ca y = f(x), funcțiile au caracteristici specifice și pot fi vizualizate folosind perechi ordonate, tabele sau grafice. Ele sunt esențiale în diferite probleme matematice și vin în diferite tipuri, inclusiv injective (unu-la-unu), surjective (pe) și bijective (ambele). Funcțiile pot fi testate utilizând testul liniei verticale și sunt clasificate în continuare în funcții polinomiale, inverse, exponențiale, logaritmice și trigonometrice. Înțelegerea funcțiilor implică recunoașterea domeniului, domeniului și regulile care le definesc. Exemplele includ funcții liniare simple, cum ar fi y = 2x + 1 și compoziții complexe de funcții. Funcțiile joacă un rol crucial în algebră, geometrie și calcul, ajutând la reprezentarea și analiza relațiilor matematice și a fenomenelor din lumea reală.

Întrebări frecvente despre Ce este o funcție

Care este definiția unei funcții?

O relație f definită într-o mulțime A cu o altă mulțime B se numește funcție în matematică dacă fiecare valoare a lui A are o valoare unică în mulțimea B.

Cum se scrie o funcție în matematică?

Funcția f în matematică este reprezentată ca f: A → B și este definită ca, f(x) = x + 2. Aici, pentru fiecare valoare unică a lui x, avem o valoare unică a lui y.

Cum se transformă o funcție?

Putem transforma cu ușurință o funcție în alte funcții prin simpla efectuare a operațiilor algebrice de bază asupra funcției. Diferitele transformări ale funcției sunt reflectarea, translația, rotația etc.

Ce este o funcție rațională?

O funcție de fracție în care numărătorul și numitorul sunt funcții polinomiale se numește funcție rațională. Câteva exemple de funcție rațională sunt:

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), etc.

Ce este o funcție liniară?

O funcție algebrică în care fiecare termen al funcției este fie constant, fie are o putere de unu se numește funcție liniară. Câteva exemple de funcție liniară sunt:

• f(x) = 2x + 3
• g(x) = x – 5 etc.

Ce sunt domeniul și codomeniul unei funcții?

Dacă definim funcția ca, y = f(x). Atunci domeniul lui x este toate valorile lui x pentru care y rezultă o valoare unică. Și co-domeniul lui y este mulțimea tuturor valorilor lui y pentru fiecare valoare a lui x.

Cum identifici o funcție în matematică?

Dacă orice valoare de intrare (x) a domeniului într-o relație are mai mult de o imagine (y), atunci aceste relații nu pot fi niciodată o funcție. Deci, dacă valoarea lui x se repetă în perechea ordonată, atunci nu este niciodată o funcție.