Numerele complexe sunt continuarea naturală a numerelor reale. În epoca modernă, numerele complexe sunt folosite în multe domenii, cum ar fi procesarea semnalului digital, criptografia și multe domenii legate de computer.

În acest articol, vom învăța despre numerele imaginare, numerele complexe și tipul acestuia, diverse operații asupra numerelor complexe, proprietățile numerelor complexe, aplicarea numerelor complexe etc.

Definiția numerelor complexe

Numere complexe sunt cele numere a formei (a + i b) Unde A & b sunt numerele reale și i este o unitate imaginară numită iota care reprezintă √-1. De exemplu, 2 + 3i este un număr complex în care 2 este un număr real și 3i este un număr imaginar. Numerele complexe pot fi scrise ca a + ib unde a și b sunt numere raționale care pot fi reprezentate pe o linie numerică care se extinde până la infinit .

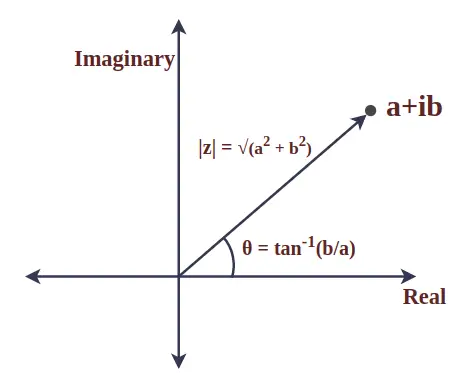
Modulul numărului complex

Modulul numărului complex este valoarea absolută și reprezintă distanța dintre origine și punctul dat. Este cunoscută și sub numele de mărimea numărului complex. Să considerăm un număr complex z = a + ib, atunci modulul lui z este definit ca:

|z| = √(a ² + b ² )

Unde,

• A este partea reală a numărului complex z și
• b este partea imaginară a numărului complex z.

Argument al numărului complex

Unghiul dintre vectorul rază al unui număr complex și axa x pozitivă se numește argumentul unui număr complex. Pentru un număr complex z = a + ib, este dat matematic de:

θ = bronz ^-1 (b/a)

Unde,

• A este partea reală a numărului complex z și
• b este partea imaginară a numărului complex z.

Puterea lui i(iota)

i(iota) este definită ca rădăcina pătrată a lui -1. Astfel, orice putere a lui i poate fi exprimată ca o multiplicare repetată a lui i de la sine, adică,

• i = √(-1)
• i²= -1
• i³= – i
• i⁴= 1
• i⁵= i
• i⁶= – 1
• și așa mai departe..

Nevoia de numere complexe

În antichitate, oamenii cunoșteau doar numerele naturale ca acestea numere sunt cele mai intuitive în natură, deoarece creierul uman le înțelege deja folosind elemente vizuale precum oile și alimentele. Astfel, avem doar mulțimea numerelor naturale ( N ) dar în numerele naturale, nu există o soluție pentru ecuația x + a = b (a> b) și a, b ∈ N. Astfel, a apărut o extensie a numerelor naturale, adică numere întregi( eu ).

Acum, din nou, în această mulțime de numere, nu există nicio soluție pentru ecuația, ax = b (a ≠ 0) și a, b ∈ I, unde a și b sunt ambele numere întregi. Astfel, o mulțime de numere întregi (I) este extinsă la o mulțime de numere raționale ( Q ).

Din nou, în această mulțime de numere raționale, nu există o soluție pentru ecuația x²= a (a> 0) și a ∈ Q. Astfel, Q este extinsă pentru a include numere astfel încât, x²= a(pentru a> 0), adică numere iraționale. Acest set este numit Numere reale și este reprezentat de R .

Acum, s-a crezut multă vreme că nu trebuie să extindem acest set de numere reale pentru a forma un alt set mai mare, deoarece această colecție de numere pare completă. Dar din nou o nouă problemă a apărut în acest set de numere, adică nu există un număr real astfel încât x²= a (a <0) și a ∈ R. Astfel, mulțimea numerelor reale este extinsă și mai mult pentru a include toate astfel de valori evaluate și denumite această mulțime de numere complexe și este reprezentată prin C .

Clasificarea numerelor complexe

După cum știm, forma standard a unui număr complex este z = (a + i b) unde a, b ∈ R și i este iota (o unitate imaginară). Deci, în funcție de valorile lui a (numită parte reală) și b (numită parte imaginară), numerele complexe sunt clasificate în patru tipuri:

• Număr complex zero
• Numere pur reale
• Numere pur imaginare
• Numere imaginare

Să învățăm despre aceste tipuri în detaliu.

Număr complex zero

Pentru orice număr complex z = a + ib dacă a = 0 & b = 0, atunci numărul complex se numește număr complex zero. De exemplu, singurul exemplu în acest sens este 0.

Numere pur reale

Pentru orice număr complex z = a + ib dacă a ≠ 0 & b = 0, atunci numărul complex se numește un număr pur real, adică un număr fără parte imaginară. Toate numerele reale sunt exemple în acest sens, astfel încât 2, 3, 5, 7 etc.

Numere pur imaginare

Pentru orice număr complex z = a + ib dacă a = 0 & b ≠ 0, atunci un număr complex se numește număr pur imaginar, adică un număr fără parte reală. Toate numerele fără părți reale sunt exemple ale acestui tip de număr, adică -7i, -5i, -i, i, 5i, 7i etc.

Numere imaginare

Pentru orice număr complex z = a + ib dacă a ≠ 0 & b ≠ 0, atunci un număr complex se numește număr imaginar . De exemplu, (-1 – i), (1 + i), (1 – i), (2 + 3i), etc.

Diferite forme de numere complexe

Există diferite forme de numere complexe care sunt,

vârsta pete davidson

• Formă dreptunghiulară
• Forma polară
• Forma exponenţială

Acum să învățăm despre ele în detaliu.

Formă dreptunghiulară

Formă dreptunghiulară este numit si Forma standard si este reprezentata de (a + ib), unde a și b sunt numerele reale.

De exemplu: (5 + 5i), (-7i), (-3 – 4i), etc.

Forma polară

Forma polară este reprezentarea unui număr complex în care coordonatele polare [unde coordonatele sunt reprezentate ca (r, θ), unde r este distanța de la origine și θ este unghiul dintre linia care unește punctul și originea și axa x pozitivă) sunt folosite pentru a reprezenta un număr complex. Orice număr complex este reprezentat ca r [cos θ + i sin θ].

De exemplu: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] etc.

Forma exponenţială

Forme exponențiale ale numerelor complexe este reprezentarea numerelor complexe folosind formula lui Euler și în această formă numărul complex este reprezentat prin reⁱ, unde r este distanța unui punct de la origine și θ este unghiul dintre axa x pozitivă și vectorul rază.

De exemplu: eⁱ⁽⁰⁾, Este^i(π/2), 5.e^i(π/6), etc.

Notă: Toate cele trei forme ale numerelor complexe discutate mai sus sunt interconvertibile, adică acestea pot fi convertite dintr-o formă în alta foarte ușor.

Operații pe numere complexe

Următoarele operații pot fi efectuate pe numere complexe:

• Plus
• Scădere
• Multiplicare
• Divizia
• Conjugare

Adunarea numerelor complexe

Putem adăuga două numere complexe, adunând pur și simplu părțile lor reale și imaginare separat.

De exemplu, (3 + 2i) + (1 + 4i) = 4 + 6i.

Scăderea numerelor complexe

Putem scădea două numere complexe, pur și simplu scăzând separat părțile lor reale și imaginare.

De exemplu, (3 + 2i) – (1 + 4i) = 2 – 2i.

Înmulțirea numerelor complexe

Putem înmulți două numere complexe folosind proprietatea distributivă și faptul că i²= -1.

De exemplu, (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Împărțirea numerelor complexe

Putem împărți un număr complex la altul, prin simpla înmulțire atât a numărătorului, cât și a numitorului cu conjugatul complex al numitorului și simplificând în continuare expresia.

De exemplu, (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Conjugarea numerelor complexe

Putem găsi cu ușurință conjugatul unui număr complex, prin simpla schimbare a semnului părții sale imaginare. Conjugatul unui număr complex este adesea notat cu o bară deasupra numărului, cum ar fi z̄.

De exemplu, conjugatul lui 3 + 2i este 3 – 2i.

Identități pentru numere complexe

Pentru oricare două numere complexe z₁și z₂pot fi date următoarele identități algebrice:

• (Cu ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Cu ₁ - Cu ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Cu ₁ ) ² - (Cu ₂ ) ² = (z ₁ + z ₂ )(Cu ₁ - Cu ₂ )
• (Cu ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Cu ₂ +3(z ₂ ) ² Cu ₁ + (z ₂ ) ³
• (Cu ₁ - Cu ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² Cu ₂ +3(z ₂ ) ² Cu ₁ - (Cu ₂ ) ³

Formule legate de numere complexe

Există câteva formule legate de numerele complexe, dintre care unele sunt după cum urmează:

Formula lui Euler

Formula lui Euler arată relația dintre puterea imaginară a exponentului și raportul trigonometric sin și cos și este dată de:

Este ^ix = cos x + i sin x

Formula lui De Moivre

Formula lui De Moivre exprimă n^thputerea unui număr complex în formă polară și este dată de:

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

Plan complex

Planul pe care numerele complexe sunt reprezentate în mod unic se numește plan complex sau plan Argand sau plan gaussian.

Planul complex are două axe:

• Axa X sau Axa Reală
• Axa Y sau Axa Imaginară

Axa X sau Axa Reală

• Toate numerele complexe pur reale sunt reprezentate unic printr-un punct pe el.
• Partea reală Re(z) a tuturor numerelor complexe sunt reprezentate grafic în raport cu aceasta.
• De aceea se mai numește și axa X Axa reală .

Axa Y sau Axa Imaginară

• Toate numerele complexe pur imaginare sunt reprezentate în mod unic printr-un punct pe el.
• Partea imaginară Im(z) a tuturor numerelor complexe este reprezentată grafic în raport cu aceasta.
• De aceea se mai numește și axa Y Axa imaginară .

diagrama modelului e-r

Reprezentarea geometrică a numerelor complexe

După cum știm că fiecare număr complex (z = a + i b) este reprezentat de un punct unic p(a, b) pe planul complex și fiecare punct din planul complex reprezintă un număr complex unic.

Pentru a reprezenta orice număr complex z = (a + i b) pe plan complex, urmați aceste convenții:

• Partea reală a lui z (Re(z) = a) devine coordonata X a punctului p

• Partea imaginară a lui z (Im(z) = b) devine coordonata Y a punctului p

Și în final z (a + i b) ⇒ p (a, b) care este un punct pe planul complex.

Proprietățile numerelor complexe

Există diverse proprietăți ale numerelor complexe, dintre care unele sunt după cum urmează:

• Pentru orice număr complex z = a + ib, dacă z = 0, atunci a = 0, precum și b = 0.
• Pentru 4 numere reale a, b, c și d astfel încât z₁= a + ib și z₂= c + id. Dacă z₁= z₂atunci a = c și b = d.
• Adunarea unui număr complex cu conjugatul său are ca rezultat un număr pur real, adică z + z̄ = Număr real.

Fie z = a + ib,

z + z̄ = a + unu + a – unu

⇒ z + z̄ = 2a (care este pur real)

• Produsul unui număr complex cu rezultatele sale conjugate este, de asemenea, un număr pur real, adică z × z̄ = Număr real

Fie z = a + ib, atunci

z × z̄ = (a + unu) × (a – unu)

⇒ z × z̄= a²– i²b²

⇒ z × z̄ = a²+ b²(care este pur real)

• Numerele complexe sunt comutativ sub operaţia de adunare şi înmulţire. Să considerăm două numere complexe z₁și z₂, și apoi

Cu ₁ +z ₂ = z ₂ +z ₁

Cu ₁ × z ₂ = z ₂ × z ₁

• Numerele complexe sunt asociativ cu operaţia de adunare şi înmulţire. Să luăm în considerare trei numere complexe z₁, Cu₂, și z₃apoi

(Cu ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Cu ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Numerele complexe dețin proprietate distributivă de înmulţire peste adunare de asemenea. Să luăm în considerare trei numere complexe z₁, Cu₂, și z₃apoi

Cu ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Citeşte mai mult,

• Împărțirea numerelor complexe
• Bara Z în numere complexe

Exemple despre numere complexe

Exemplul 1: Trasează aceste numere complexe z = 3 + 2i pe planul Complex.

Soluţie:

Dat:

Cu = 3 + 2 i

Deci, punctul este z(3, 2). Acum reprezentăm acest punct pe graficul de mai jos, aici în acest grafic axa x reprezintă partea reală, iar axa y reprezintă partea imaginară.

Exemplul 2: Trasează aceste numere complexe z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) pe planul Complex.

Soluţie:

Dat:

Cu₁= (2 + 2 i)

Cu₂= (-2 + 3 i)

Cu₃= (-1 – 3 i)

Cu₄= (1 – i)

Deci, punctele sunt z₁(2, 2), z₂(-2, 3), z₃(-1, -3) și z₄(1, -1). Acum reprezentăm aceste puncte pe graficul de mai jos, aici în acest grafic axa x reprezintă partea reală, iar axa y reprezintă partea imaginară.

Întrebări frecvente despre numerele complexe

Definiți numerele complexe.

Numerele de forma a+ib se numesc număr complex, unde a și b sunt numărul real și i este unitatea imaginară care reprezintă rădăcina pătrată a lui -1.

Care este diferența dintre un număr real și un număr complex?

Diferența dintre numerele reale și complexe este că avem nevoie doar de un număr pentru a reprezenta orice număr real, dar avem nevoie de două numere reale pentru a reprezenta orice număr complex.

Care este partea reală și partea imaginară a unui număr complex?

Într-un număr complex a + ib, a este partea reală a numărului complex, iar b este numită partea imaginară a numărului complex.

Care este conjugatul complex al unui număr complex?

Pentru un număr complex a + ib, a – ib se numește conjugatul său complex. Conjugatele complexe pot fi găsite prin simpla schimbare a semnului părții imaginare.

Care este modulul unui număr complex?

Distanța dintre origine și punctul reprezentat de un număr complex în planul argand se numește modulul acelui număr complet și pentru z = a + ib, este dată matematic de:

|z| = √(a ² + b ² )

format string java

Care este argumentul unui număr complex?

Unghiul dintre vectorul rază al unui număr complex și axa x pozitivă se numește argumentul unui număr complex și pentru z = a + ib, este dat matematic de:

θ = bronz ^-1 (b/a)

Care este forma polară a unui număr complex?

Pentru orice număr complex, z = a + ib, forma polară a acestuia este dată de:

r [cos θ + i sin θ]

Care este formula lui Euler?

Formula lui Euler arată relația dintre puterea imaginară a exponentului și raportul trigonometric sin și cos și este dată de:

Este ^ix = cos x + i sin x