Tabel de trigonometrie este un tabel standard care ne ajută să găsim valorile rapoartelor trigonometrice pentru unghiuri standard, cum ar fi 0°, 30°, 45°, 60° și 90°. Aceasta constă din toate cele șase rapoarte trigonometrice: sinus, cosinus, tangentă, cosecantă, secantă și cotangentă.
Să învățăm în detaliu despre tabelul de trigonometrie.
Cuprins
- Tabel de trigonometrie
- Tabelul funcțiilor trigonometrice
- Truc pentru a învăța rapoartele trigonometrice
- Cum să memorezi tabelul trigonometric
- Cum se creează un tabel Trig
- Formule trigonometrice
- Tabelul identităților trigonometrice
- Exemple de tabele trigonometrice
Tabel de trigonometrie
Tabelul trigonometric este aranjarea valorilor tuturor celor șase funcții trigonometrice pentru unghiurile lor comune într-o formă tabelată.
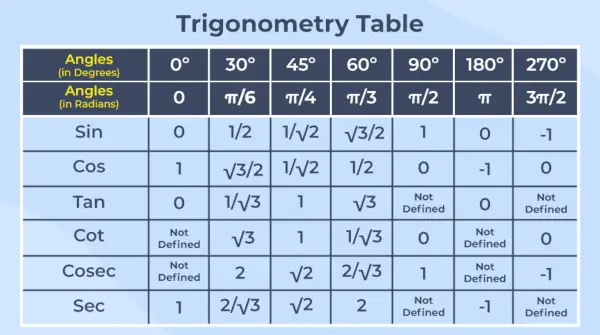
Notă – Trigonometria este o ramură a matematicii care se ocupă de relațiile dintre unghiurile și laturile triunghiurilor dreptunghiulare.
Tabelul funcțiilor trigonometrice
Trigonometria are 6 funcții trigonometrice de bază, acestea sunt sinus, cosinus, tangentă, cosecantă, secantă și cotangentă. Acum să ne uităm la funcțiile trigonometrice.
Pentru orice triunghi dreptunghic cu perpendiculară (P), bază (B) și ipotenuză (H), cele șase funcții trigonometrice sunt după cum urmează:
| Tabelul funcțiilor trigonometrice | |||
| Funcţie | Definiție | Reprezentare | Relația cu laturile unui triunghi dreptunghic |
| A lui | Raportul dintre perpendiculară și ipotenuză | fără i | Partea opusă / Hipotenuză |
| Cosinus | Raportul dintre bază și ipotenuză | cos i | Latura adiacentă / Hipotenuză |
| Tangentă | Raportul dintre sinus și cosinus al unghiului | asa de i | Partea opusă / Partea adiacentă |
| Cosecant | Reciprocul sin θ | csc i sau cosec i | Hipotenuză / Partea opusă |
| Secantă | Reciproc al cos θ | sec i | Hipotenuză / Latura adiacentă |
| Cotangent | Reciproc de tan θ | pat i | Latura adiacentă / Latura opusă |
Notă – Trigonometria este o ramură a matematicii care se ocupă cu relațiile dintre unghiurile și laturile triunghiurilor, în special triunghiurile dreptunghiulare. Implica studiul și aplicarea funcțiilor sinus, cosinus, tangente și alte funcții trigonometrice pentru a rezolva probleme din diverse domenii.
Verifica : Trigonometrie: formule, tabel, identități și rapoarte
redenumiți un director linux
Truc pentru a învăța rapoartele trigonometrice
Studiați tabelul discutat mai jos pentru a afla rapoartele trigonometrice într-un mod ușor de reținut.
| Unii oameni au părul negru creț pentru a produce frumusețe |
| sin θ (Unii) = Perpendiculară (oameni) / ipotenuză (au) |
| cos θ (creț) = Bază (neagră) / ipotenuză (păr) |
| tan θ (la) = Perpendicular (produce) / Bază (frumusețe) |
Cum să memorezi tabelul trigonometric
Tabelul de trigonometrie este destul de ușor de reținut dacă cunoașteți toate formulele de trigonometrie. Există, de asemenea, un truc numit truc cu o singură mână pentru a memora tabelul de trigonometrie.

Pasul 1: În figura de mai sus, pentru tabelul sinusurilor, numărați degetele din partea stângă pentru unghiul standard.
Pasul 2: Împărțiți numărul de degete din partea stângă (calculați în primul pas) la 4
Pasul 3: Găsiți rădăcina pătrată a valorii calculate la pasul 2.
Verifica: Formule de trigonometrie – Lista tuturor identităților și formulelor trigonometrice
Cum se creează un tabel Trig
Studiați următorii pași pentru a crea tabelul trigonometric pentru unghiuri standard.
Pasul 1: Creați tabelul
Creați un tabel și enumerați toate unghiurile, cum ar fi 0°, 30°, 45°, 60° și 90°, în rândul de sus. Introduceți toate funcțiile trigonometrice sin, cos, tan, cosec, sec și cot în prima coloană.
Pasul 2: Evaluați valoarea pentru toate unghiurile funcției sin.
Pentru a găsi valorile funcției sin, împărțiți 0, 1, 2, 3 și 4 la 4 și luați sub rădăcina fiecărei valori, respectiv ca:
Pentru, valoarea de sin 0° = √(0/4) = 0
În mod similar,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| fără 0° | fără 30° | fără 45° | fără 60° | fără 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Pasul 3: Evaluați valoarea pentru toate unghiurile funcției cos
Valoarea funcției cos este opusă valorii funcției sin, adică cos 0° = sin 90°, cos 30° = sin 60° și cos 45° = sin 45°, deci
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Pasul 4: Evaluați valoarea pentru toate unghiurile funcției bronz
Valoarea funcției tan este egală cu funcția sin împărțită la funcția cos, adică tan x = sin x / cos x. Valoarea tuturor unghiurilor din funcția tan este calculată ca:
tan 0°= sin 0° / cos 0° = 0/1 = 0, la fel
| deci 0° | deci 30° | deci 45° | deci 60° | deci 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Nedefinit |
Pasul 5: Evaluați valoarea pentru toate unghiurile funcției cosec
Valoarea funcției cosec este egală cu reciproca funcției sin. Valoarea cosec 0° se obține luând reciproca sin 0°
cosec 0° = 1 / sin 0° = 1 / 0 = Nedefinit. În mod similar,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Nedefinit | 2 | √2 | 23 | 1 |
Pasul 6: Evaluați valoarea pentru toate unghiurile funcției sec
Valoarea funcției sec este egală cu reciproca funcției cos. Valoarea sec 0° se obține luând reciproca cos 0°
sec 0° = 1 / cos 0° = 1 / 1 = 1. În mod similar,
| sec 0° | sec 30° | sec 45° | sec 60° | sec 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Nedefinit |
Pasul 7: Evaluați valoarea pentru toate unghiurile funcției de pat
Valoarea funcției cot este egală cu reciproca funcției tan. Valoarea cot 0° se obține luând reciproca lui tan 0°
cot 0° = 1 /tan 0° = 1 / 0 = Nedefinit. În mod similar,
| patut 0° | patut 30° | pătuț 45° | pătuț 60° | patut 90° |
|---|---|---|---|---|
| Nedefinit | √3 | 1 | 1/√3 | 0 |
În acest fel, putem crea următorul tabel cu rapoarte trigonometrice:
| Tabel trigonometric cu grade și radiani | |||||||
|---|---|---|---|---|---|---|---|
| Unghi (în grade) | Unghi (în radiani) | Fără | Cos | Asa de | Cosec | Sec | Pat |
| 0° | 0 | 0 | 1 | 0 | Nedefinit | 1 | Nedefinit |
| 30° | p/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Nedefinit | 1 | Nedefinit | 0 |
Formule trigonometrice
Să învățăm despre câteva formule de trigonometrie legate de unghiurile complementare și suplimentare.
- Unghiuri complementare: Pereche de unghiuri a căror sumă este egală cu 90°
- Unghiuri suplimentare: Pereche de unghiuri a căror sumă este egală cu 180°
Verifica: Raporturi trigonometrice
Identități de declanșare ale unghiurilor complementare
Identitățile unghiurilor complementare se bazează pe relația dintre funcțiile trigonometrice a două unghiuri care însumează până la 90 de grade (sau π/2 radiani). Acestea sunt cunoscute ca identități co-funcționale .
| Funcția trigonometrică | Identitate |
|---|---|
| A lui | sin(90°− i )=cos i |
| Cosinus | cos(90°− i )=fara i |
| Tangentă | tan(90°− i )=cot i |
| Cotangent | pat (90°− i )=deci i |
| Secantă | sec(90°− i )=csc i |
| Cosecant | cosec(90°− i )=sec i |
Identități de declanșare ale unghiurilor suplimentare
Identitățile unghiurilor suplimentare se referă la funcțiile trigonometrice a două unghiuri care însumează până la 180 de grade (sau π radiani).
| Funcția trigonometrică | Identitate |
|---|---|
| A lui | sin(180°− i )=fara i |
| Cosinus | cos(180°− i )=−cos i |
| Tangentă | bronz (180°− i )=−tan i |
| Cotangent | pat (180°− i )=−cot i |
| Secantă | sec(180°− i )=−sec i |
| Cosecant | cosec(180°− i )=cosec i |
Tabelul identităților trigonometrice
Identități trigonometrice sunt identitățile care sunt foarte utilizate în rezolvarea problemelor trigonometrice. Există diverse identități trigonometrice, dar cele trei identități trigonometrice principale sunt:
| Tabelul identităților trigonometrice | |
| Identitatea trigonometrică | Formulă |
| Identitatea pitagoreică | fără2θ + cos2θ = 1 |
| Identitate secant-tangentă | sec2θ – deci2θ = 1 |
| Identitate Cosecant-Cotangentă | cosec2θ – pătuț2θ = 1 |
De asemenea, verificați:
- Raporturi trigonometrice
- Identități trigonometrice inverse
- Înălțimi și distanțe
Exemple de tabele trigonometrice
Să rezolvăm câteva întrebări pe tabelul trigonometric.
Exemplul 1: Dacă sin θ = 4/5, atunci găsiți toate valorile trigonometrice.
Soluţie:
Aici avem,
sin θ = 4/5
qiuck sortas, sin θ = Perpendiculară / Hipotenuză
deci avem Perpendiculara (P)= 4 si ipotenuza(H) = 5
Deci, conform teoremei lui Pitagora H 2 = P 2 +B 2
Să aflăm valoarea bazei (B)
52= B2+ 42
25 = B2+ 16
25 -16 = B2
B2= 9
B = 3Acum avem,
Sin θ = Perpendiculară/Hipotenuză
= AB/AC = 4/5Cosinus θ = Baza/Hipotenuza
= BC/AC = 3/5Tangenta θ = Perpendiculara/Baza
= AB/BC = 4/3Cosecantă θ = Hipotenuză/Perpendiculară
= AC/AB = 5/4Secanta θ = Hipotenuză/Bază
= AC/BC = 5/3Cotangentă θ = Bază/Perpendiculară
= BC/AB = 3/4
Exemplul 2: Aflați valoarea cos 45° + 2 sin 60° – tan 60°.
Soluţie:
Din tabelul de trigonometrie,
cos 45° = 1/√2, sin 60° = √3/2 și tan 60° = √3
Prin urmare,
cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Exemplul 3: Găsiți valoarea cos 75°.
Soluţie:
Noi stim aia,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Concluzie – Tabel de trigonometrie
Tabelul de trigonometrie oferă o referință cuprinzătoare pentru funcțiile trigonometrice sinus, cosinus, tangent, cosecant, secant și cotangent, împreună cu valorile lor respective pentru diferite unghiuri. eu t servește ca un instrument valoros pentru rezolvare ecuații trigonometrice, analiza relațiilor geometrice și înțelegerea comportamentului fenomenelor periodice. Fie în matematică, fizică, inginerie sau alte domenii, tabelul de trigonometrie ajută la calcule, rezolvarea problemelor și vizualizare, contribuind la o înțelegere mai profundă a conceptelor trigonometrice și a aplicațiilor acestora în scenarii din lumea reală.
Tabel de trigonometrie – Întrebări frecvente
Ce este trigonometria?
Trigonometria este ramura matematicii care se ocupă cu unghiurile și laturile oricărui triunghi.
Ce este un tabel trigonometric?
Tabelul de trigonometrie este un tabel care conține valorile tuturor celor șase funcții trigonometrice pentru unghiurile comune.
Cine a inventat masa de trigonometrie?
astronomul grec Hipparchus (127 î.Hr.) a inventat tabelul de trigonometrie.
Ce sunt unghiurile standard într-un tabel trigonometric?
Unghiurile standard dintr-un tabel trigonometric sunt 0°, 30°, 45°, 60° și 90°
Care este valoarea bronzului de 45 de grade?
Valoarea bronzului 45 de grade este 1.
Cum să înveți tabelul de trigonometrie?
Trucul pentru învățarea tabelului trigonometric este,
- Trebuie să înveți toate valorile tuturor unghiurilor funcției sin.
- Valoarea tuturor unghiurilor funcției cos este imaginea în oglindă a funcției sin.
- Valorile funcției tan pot fi calculate prin împărțirea funcției sin la funcția cos.
- Valoarea funcției cosec este reciprocă a sin.
- În mod similar, sec și cot sunt reciproce ale funcției cos și cot.
Care sunt șase funcții de bază în tabelul trigonometric?
Cele șase funcții trigonometrice de bază din tabelul trigonometric sunt Sinus, Cosinus, Tangent, Secant, Cotangent și Cosecant.
Există calculatoare care pot înlocui tabelele de trigonometrie?
Calculatoarele științifice pot calcula rapoarte trigonometrice pentru orice unghi8.
La ce folosește un tabel de trigonometrie?
Tabelul de trigonometrie este folosit practic pentru a găsi valorile tuturor rapoartelor trigonometrice pentru toate unghiurile. Aceste valori au o serie de aplicații în viața reală.
