Un NFA poate avea zero, una sau mai multe mișcări dintr-o stare dată pe un simbol de intrare dat. Un NFA poate avea și mișcări NULL (mușcări fără simbol de intrare). Pe de altă parte, DFA are o singură mișcare dintr-o stare dată pe un simbol de intrare dat.
t flip flop
Pași pentru conversia NFA în DFA:
Pasul 1: Convertiți NFA dat în tabelul său de tranziție echivalent
Pentru a converti NFA în tabelul său de tranziție echivalent, trebuie să listăm toate stările, simbolurile de intrare și regulile de tranziție. Regulile de tranziție sunt reprezentate sub forma unei matrice, unde rândurile reprezintă starea curentă, coloanele reprezintă simbolul de intrare, iar celulele reprezintă starea următoare.
Pasul 2: creați starea de pornire a DFA
Starea de început a DFA este setul tuturor stărilor de început posibile în NFA. Acest set se numește închiderea epsilon a stării de pornire a NFA. Închiderea epsilonului este ansamblul tuturor stărilor care pot fi atinse din starea de început urmând tranzițiile epsilon (?).
Pasul 3: creați tabelul de tranziție al DFA
Tabelul de tranziție al DFA este similar cu tabelul de tranziție al NFA, dar în loc de stări individuale, rândurile și coloanele reprezintă seturi de stări. Pentru fiecare simbol de intrare, celula corespunzătoare din tabelul de tranziție conține închiderea epsilonului setului de stări obținute prin respectarea regulilor de tranziție din tabelul de tranziție al NFA.
Pasul 4: creați stările finale ale DFA
Stările finale ale DFA sunt seturile de stări care conțin cel puțin o stare finală din NFA.
Pasul 5: simplificați DFA
DFA obținut în pașii anteriori poate conține stări și tranziții inutile. Pentru a simplifica DFA, putem folosi următoarele tehnici:
- Eliminați stările inaccesibile: statele care nu pot fi atinse din starea de început pot fi eliminate din DFA.
- Eliminați statele moarte: statele care nu pot duce la o stare finală pot fi eliminate din DFA.
- Îmbinarea stărilor echivalente: Statele care au aceleași reguli de tranziție pentru toate simbolurile de intrare pot fi îmbinate într-o singură stare.
Pasul 6: Repetați pașii 3-5 până când nu mai este posibilă nicio simplificare
După simplificarea DFA, repetăm pașii 3-5 până când nu mai este posibilă nicio simplificare. DFA final obținut este echivalentul DFA minimizat cu NFA dat.
Exemplu: Luați în considerare următorul NFA prezentat în Figura 1.

Mai jos sunt diferiți parametri pentru NFA. Q = { q0, q1, q2 } ? = ( a, b ) F = { q2 } ? (Funcția de tranziție a NFA)
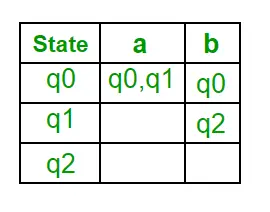
Pasul 1: Q’ = ? Pasul 2: Q’ = {q0} Pasul 3: Pentru fiecare stare din Q’, găsiți stările pentru fiecare simbol de intrare. În prezent, starea în Q’ este q0, găsiți mișcările de la q0 pe simbolul de intrare a și b folosind funcția de tranziție a NFA și actualizați tabelul de tranziție a DFA. ?’ (Funcția de tranziție a DFA)

Acum { q0, q1 } va fi considerat ca o singură stare. Deoarece intrarea sa nu este în Q’, adăugați-o la Q’. Deci Q' = { q0, { q0, q1 } } Acum, mișcările din starea { q0, q1 } pe diferite simboluri de intrare nu sunt prezente în tabelul de tranziție al DFA, îl vom calcula astfel: ( { q0, q1 } , a ) = ? ( q0, a ) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? ( q0, b ) ? ? ( q1, b ) = { q0, q2 } Acum vom actualiza tabelul de tranziție al DFA. ?’ (Funcția de tranziție a DFA)

Acum { q0, q2 } va fi considerat ca o singură stare. Deoarece intrarea sa nu este în Q’, adăugați-o la Q’. Deci Q' = { q0, { q0, q1 }, { q0, q2 } } Acum, mișcările din starea {q0, q2} pe diferite simboluri de intrare nu sunt prezente în tabelul de tranziție al DFA, le vom calcula astfel: ?' ( { q0, q2 }, a ) = ? ( q0, a ) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? ( q0, b ) ? ? ( q2, b ) = { q0 } Acum vom actualiza tabelul de tranziție al DFA. ?’ (Funcția de tranziție a DFA)
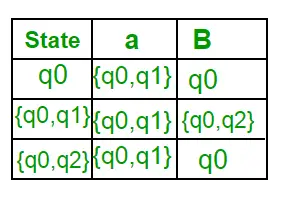
Deoarece nu este generată nicio stare nouă, am terminat cu conversia. Starea finală a DFA va fi starea care are q2 ca componentă, adică { q0, q2 } Mai jos sunt diferiți parametri pentru DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } și funcția de tranziție ?’ așa cum se arată mai sus. DFA final pentru NFA de mai sus a fost prezentat în Figura 2.
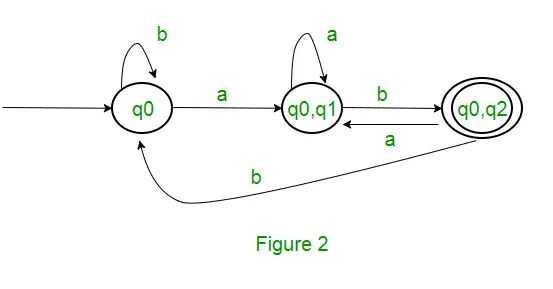
Notă : Uneori, nu este ușor să convertiți expresiile regulate în DFA. Mai întâi puteți converti expresia regulată în NFA și apoi NFA în DFA.
intrebare: Numărul de stări în automatul finit determinist minim corespunzător expresiei regulate (0 + 1)* (10) este ____________.
factorial în c
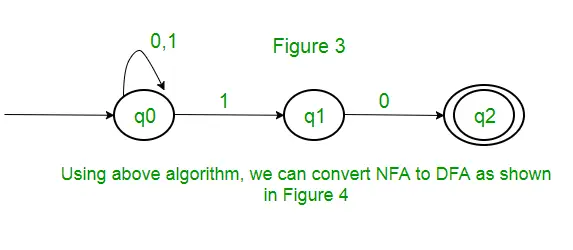
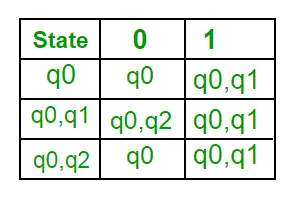
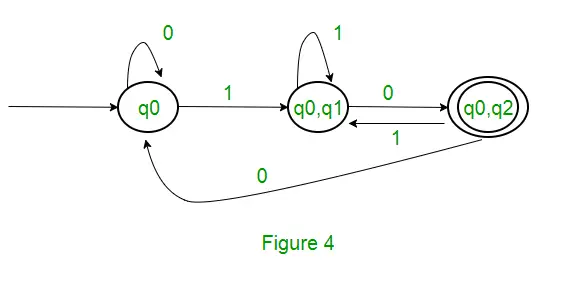
Solutie: În primul rând, vom face un NFA pentru expresia de mai sus. Pentru a face un NFA pentru (0 + 1)*, NFA va fi în aceeași stare q0 pe simbolul de intrare 0 sau 1. Apoi, pentru concatenare, vom adăuga două mișcări (q0 la q1 pentru 1 și q1 la q2 pentru 0) așa cum se arată în figura 3.
Acest articol a fost contribuit de Sonal Tuteja.
