Un cerc este format din puncte care sunt toate la aceeași distanță de centrul cercului. O formă geometrică închisă este un cerc. În viața de zi cu zi, vedem cercuri sub formă de roată, pizza, un pământ rotund și așa mai departe.

Părți ale unui cerc

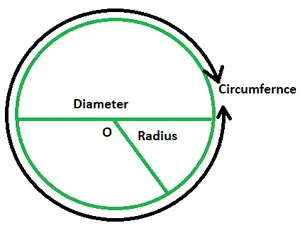
Termeni cheie:

• Rază: The raza unui cerc este distanța dintre centrul său și orice punct de pe margine. În general este notat ca r. Un cerc are un număr nesfârșit de raze.
• Diametru: Este o linie care trece prin centru și își are capetele pe cerc. Este notat cu D și este de două ori valoarea razei cercului.
• Circumferinţă: Întinderea graniței cercului este egală cu circumferința acestuia. Aceasta înseamnă că perimetrul unui cerc este egal cu circumferința acestuia. Circumferința cercului va fi egală cu lungimea firului care se înfășoară perfect în jurul perimetrului său. Este dat ca 2πr.

Care este aria cercului?

Aria unui cerc se referă la cantitatea de spațiu cuprinsă de marginea unui cerc. Zona umplută de cerc este teritoriul din perimetrul cercului. Este cunoscută și ca cantitatea totală de unități pătrate incluse în cerc.

Verifica: Diametrul unui cerc

Zone de formule cerc

Aria suprafeței unui cerc este dată de următoarea formulă:

mvc java

A = πr ²

unde r este raza cercului dat.

sau

A = C ² /4p

unde C este circumferința cercului dat.

Exemple folosind Formula Ariei Cercului

Întrebarea 1. Aflați aria unui cerc având în vedere că raza lui este de 8 m.

Soluţie:

Dat: r = 8 m

Deoarece aria unui cerc = πr²

A = π(8)²

exemple de programe java

= 64p

= 200,96 m ²

Întrebarea 2. Aflați aria unui cerc având în vedere circumferința lui 12 cm.

Soluţie:

Dat: C = 12 cm

Deoarece, A = C²/4p

= 12²/4p

= 11,46 cm ²

Întrebarea 3. Aflați aria unui cerc având în vedere diametrul său de 12 cm.

Soluţie:

Dat: D = 12 cm

c matrice de șiruri de program

sau, Raza = r = 12/2 = 6 cm

Deoarece A = πr²

= π(6)2

= 113,04 cm ²

Întrebarea 4. Aflați aria unui cerc având în vedere că raza lui este de 9 cm.

Soluţie:

if else if else if java

Dat: r = 9 m

Deoarece aria unui cerc = πr²

A = π(9)²

= 81p

= 254,34 cm ²

Întrebarea 5. Aflați aria unui cerc având în vedere diametrul său de 10 cm.

Soluţie:

Dat: D = 10 cm

sau, Raza = r = 10/2 = 5 cm

Deoarece A = πr²

= π(5)²

jquery acest clic

= 78,5 cm ²

Verificați și:

• Calculator pentru suprafața unui cerc
• Meci pătrați a Calculatorului de cerc
• Calculator pentru raza unui cerc
• Diametrul unui cerc Calculator
• Calculator de circumferință
• Calculator circumferință la diametru