În acest articol, vom discuta traversarea în ordine în structura datelor.
Dacă vrem să parcurgem nodurile în ordine crescătoare, atunci folosim traversarea în ordine. Următorii sunt pașii necesari pentru traversarea în ordine:
- Vizitați toate nodurile din subarborele din stânga
- Vizitați nodul rădăcină
- Vizitați toate nodurile din subarborele din dreapta
Structurile liniare de date, cum ar fi stiva, matricea, coada etc., au o singură modalitate de a parcurge datele. Dar în structurile de date ierarhice precum copac, există mai multe moduri de a parcurge datele. Aici vom discuta un alt mod de a parcurge structura de date arborescentă, adică traversarea în ordine.
Există două abordări utilizate pentru traversarea în ordine:
b plus arbore
- Parcurs în ordine folosind recursiunea
- Parcurgere în ordine folosind o metodă iterativă
O tehnică de traversare în ordine urmează Stânga Rădăcină Dreapta politică. Aici, Left Root Right înseamnă că subarborele din stânga al nodului rădăcină este parcurs mai întâi, apoi nodul rădăcină, iar apoi subarborele din dreapta al nodului rădăcină este parcurs. Aici, numele în ordine în sine sugerează că nodul rădăcină se află între subarborele din stânga și din dreapta.
Vom discuta traversarea în ordine folosind atât tehnici recursive, cât și iterative. Să începem mai întâi cu traversarea în ordine folosind recursiunea.
Parcurgere în ordine folosind recursiunea
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Exemplu de parcurgere în ordine
Acum, să vedem un exemplu de traversare în ordine. Va fi mai ușor de înțeles procedura de parcurgere în ordine folosind un exemplu.
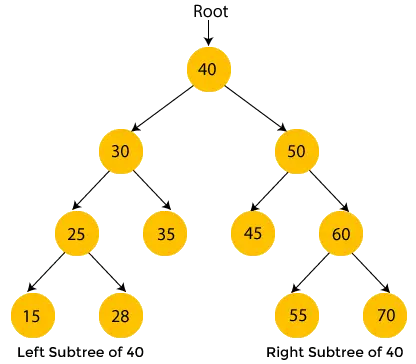
Nodurile cu culoare galbenă nu sunt încă vizitate. Acum, vom traversa nodurile arborelui de mai sus folosind traversarea în ordine.
- Aici, 40 este nodul rădăcină. Ne deplasăm la subarborele din stânga al lui 40, adică 30, și are și subarborele 25, așa că ne mutăm din nou la subarborele din stânga al lui 25, adică 15. Aici, 15 nu are subarborele, deci imprimare 15 și deplasați-vă către nodul său părinte, 25.
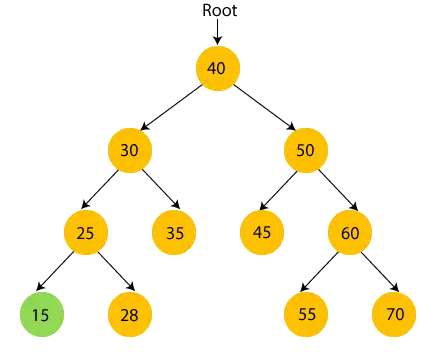
- Acum, imprimare 25 și treceți la subarborele din dreapta al lui 25.
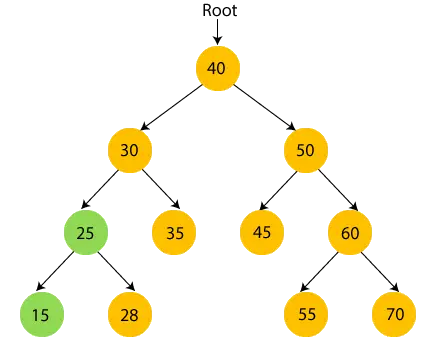
- Acum, imprimare 28 și treceți la nodul rădăcină al lui 25, adică 30.
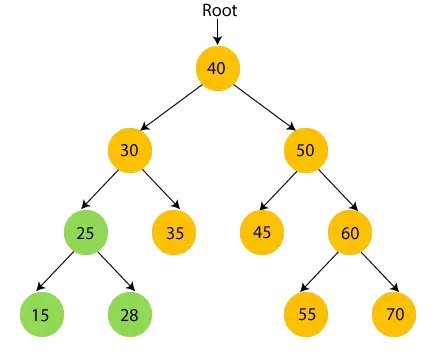
- Deci, subarborele din stânga 30 este vizitat. Acum, imprimare 30 și treceți la copilul drept de 30 de ani.
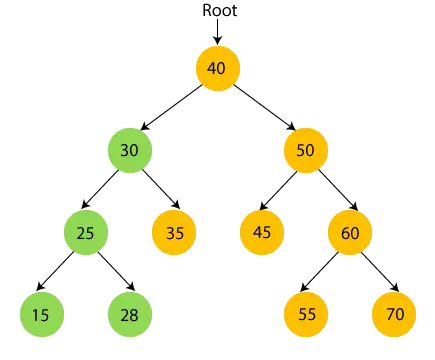
- Acum, imprimare 35 și treceți la nodul rădăcină de 30.
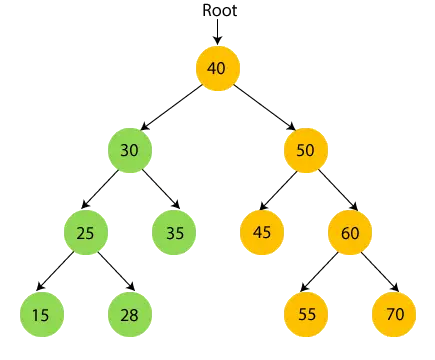
- Acum, tipăriți nodul rădăcină 40 și deplasați-vă în subarborele din dreapta.
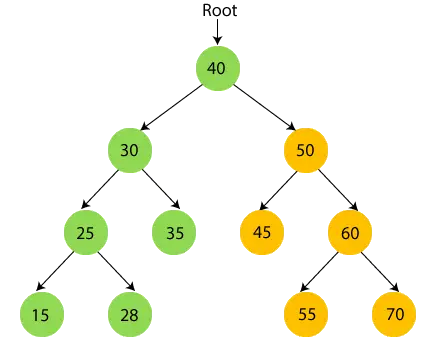
- Acum traversați recursiv subarborele din dreapta al lui 40, adică 50.
50 au subarborele, așa că mai întâi traversați subarborele din stânga lui 50, adică 45. 45 nu are copii, deci imprimare 45 și treceți la nodul său rădăcină.
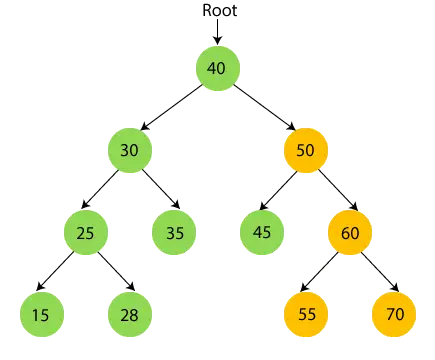
- Acum tipăriți 50 și treceți la subarborele din dreapta al lui 50, adică 60.
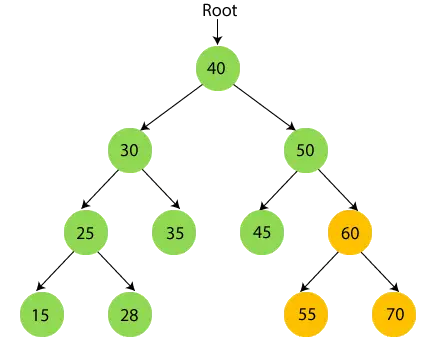
- Acum traversați recursiv subarborele din dreapta al lui 50, care este 60. 60 au subarborele, așa că mai întâi traversați subarborele din stânga al lui 60, care este 55. 55 nu are copii, deci tipăriți 55 și treceți la nodul său rădăcină.
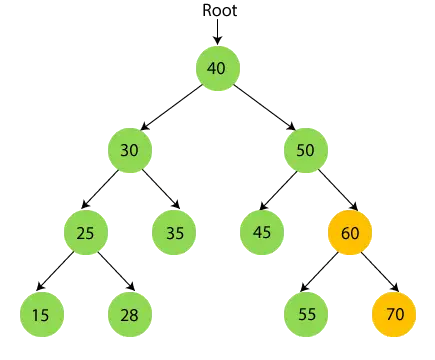
- Acum imprimare 60 și treceți la subarborele din dreapta al lui 60, adică 70.
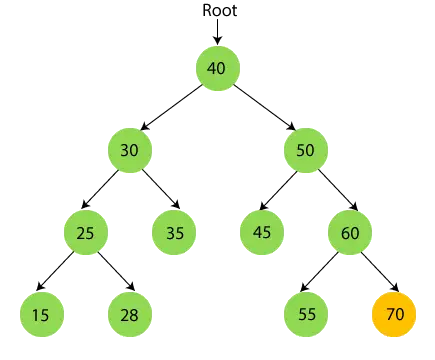
- Acum imprimare 70.
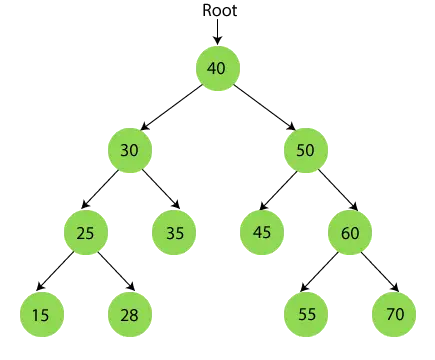
După finalizarea traversării în ordine, rezultatul final este -
if else declarație java
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Complexitatea traversării în ordine
Complexitatea temporală a traversării în ordine este Pe), unde „n” este dimensiunea arborelui binar.
Întrucât, complexitatea spațială a traversării în ordine este O(1), dacă nu luăm în considerare dimensiunea stivei pentru apelurile de funcții. În caz contrar, complexitatea spațială a traversării în ordine este Oh), unde „h” este înălțimea copacului.
Implementarea traversării în ordine
Acum, să vedem implementarea traversării în ordine în diferite limbaje de programare.
Program: Scrieți un program pentru a implementa traversarea în ordine în limbajul C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Ieșire
js onload

Program: Scrieți un program pentru a implementa traversarea în ordine în C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Ieșire

Program: Scrieți un program pentru a implementa traversarea în ordine în Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Ieșire
ce este cablat automat în java

Deci, asta e totul despre articol. Sper că articolul vă va fi util și informativ.











