- Pushdown automate este o modalitate de a implementa un CFG în același mod în care proiectăm DFA pentru o gramatică obișnuită. Un DFA își poate aminti o cantitate finită de informații, dar un PDA își poate aminti o cantitate infinită de informații.
- Pushdown automate este pur și simplu un NFA augmentat cu o „memorie stivă externă”. Adăugarea stivei este folosită pentru a oferi automatelor Pushdown o capacitate de gestionare a memoriei „ultimul intrat, primul ieșit”. Automatele Pushdown pot stoca o cantitate nelimitată de informații pe stivă. Poate accesa o cantitate limitată de informații din stivă. Un PDA poate împinge un element în partea de sus a stivei și poate scoate un element din partea de sus a stivei. Pentru a citi un element în stivă, elementele de sus trebuie să fie scoase și se pierd.
- Un PDA este mai puternic decât FA. Orice limbă care poate fi acceptată de FA poate fi acceptată și de PDA. PDA acceptă, de asemenea, o clasă de limbaj care nici măcar nu poate fi acceptată de FA. Astfel PDA este mult mai superior FA.
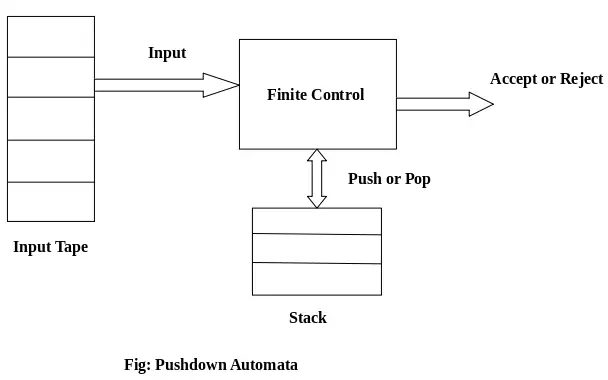
Componente PDA:
Bandă de intrare: Banda de intrare este împărțită în mai multe celule sau simboluri. Capul de intrare este doar pentru citire și se poate mișca doar de la stânga la dreapta, câte un simbol.
Control finit: Controlul finit are un indicator care indică simbolul curent care urmează să fie citit.
Grămadă: Stiva este o structură în care putem împinge și scoate articolele de la un singur capăt. Are o dimensiune infinită. În PDA, stiva este folosită pentru a stoca temporar articolele.
Definiția oficială a PDA:
PDA-ul poate fi definit ca o colecție de 7 componente:
Î: setul finit de stări
∑: setul de intrare
C: un simbol stivă care poate fi împins și scos din stivă
q0: starea initiala
string ti int
CU: un simbol de început care este în Γ.
F: un set de stări finale
d: funcția de mapare care este utilizată pentru trecerea de la starea curentă la starea următoare.
Descriere instantanee (ID)
ID este o notație informală a modului în care un PDA calculează un șir de intrare și ia decizia că șirul este acceptat sau respins.
O descriere instantanee este un triplu (q, w, α) unde:
q descrie starea actuală.
În descrie intrarea rămasă.
sortare matrice java
A descrie conținutul stivei, sus în stânga.
Notație turnichet:
Semnul ⊢ descrie notația turnichet și reprezintă o mișcare.
Semnul ⊢* descrie o succesiune de mișcări.
De exemplu,
(p, b, T) ⊢ (q, w, α)
obj în java
În exemplul de mai sus, în timp ce se face o tranziție de la starea p la q, simbolul de intrare „b” este consumat, iar partea de sus a stivei „T” este reprezentată de un șir nou α.
Exemplul 1:
Proiectați un PDA pentru acceptarea unei limbi anb2n.
Soluţie: În acest limbaj, n număr de a ar trebui să fie urmat de 2n număr de b. Prin urmare, vom aplica o logică foarte simplă, și anume dacă citim un singur „a”, vom împinge două a în stivă. De îndată ce citim „b”, atunci pentru fiecare „b” ar trebui să apară doar un „a” din stivă.
ID-ul poate fi construit după cum urmează:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa)
Acum, când citim b, vom schimba starea de la q0 la q1 și vom începe să apară „a” corespunzătoare. Prin urmare,
δ(q0, b, a) = (q1, ε)
Astfel, acest proces de apariție a „b” va fi repetat dacă nu sunt citite toate simbolurile. Rețineți că acțiunea de popping are loc numai în starea q1.
δ(q1, b, a) = (q1, ε)
După ce ați citit toate b, ar trebui să apară toate a corespunzătoare. Prin urmare, atunci când citim ε ca simbol de intrare, atunci nu ar trebui să fie nimic în stivă. Prin urmare, mutarea va fi:
δ(q1, ε, Z) = (q2, ε)
Unde
PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})
Putem rezuma ID-ul astfel:
δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε)
Acum vom simula acest PDA pentru șirul de intrare „aaabbbbbb”.
δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT
Exemplul 2:
Proiectați un PDA pentru acceptarea unei limbi 0n1m0n.
Soluţie: În acest PDA, n număr de 0 sunt urmate de orice număr de 1 urmat de n număr de 0. Prin urmare, logica pentru proiectarea unui astfel de PDA va fi următoarea:
Împingeți toate 0-urile în stivă când întâlniți primele 0-uri. Atunci, dacă citim 1, nu facem nimic. Apoi citiți 0 și la fiecare citire a 0, scoateți unul 0 din stivă.
eroare de atribut python
De exemplu:

Acest scenariu poate fi scris sub forma ID ca:
δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state)
Acum vom simula acest PDA pentru șirul de intrare „0011100”.
δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT
