cel Funcția cosinus sau cos funcția pe scurt este una dintre cele șase Funcții trigonometrice fundamental pentru trigonometrie. Cosinusul în trigonometrie este dat ca raport dintre bază și ipotenuza unui triunghi dreptunghic. Funcția cosinus este reprezentată ca Cos x unde x este unghiul pentru care se calculează raportul cosinus. Din punct de vedere al funcției, putem spune că x este intrarea sau domeniul funcției cosinus.

Este utilizat pe scară largă într-o gamă largă de subiecte, cum ar fi fizică, geometrie și inginerie, printre altele, în general, prin valorificarea naturii sale periodice. De exemplu, este folosit pentru a defini natura ondulatorie a undelor sonore, calculele fluxului electric printr-o suprafață plană etc. În acest articol, aflăm în detaliu despre ce este funcția cosinus, domeniul și domeniul a funcției cosinus, a perioadei și graficul funcției cosinus.

Cuprins

• Ce este funcția cosinus?
• Cos în Cercul Unității
• Graficul funcției cosinus
• Inversa funcției cosinus
• Funcția cosinus în calcul
• Identitățile funcției Cos

Ce este funcția cosinus?

Funcția cosinus este o funcție trigonometrică care este practic periodică în natură. Funcția cosinus este exprimată ca cos x unde x este unul dintre unghiurile ascuțite ale unui triunghi dreptunghic. Funcția cosinus găsește raportul dintre bază și ipotenuză pentru o valoare dată a lui x. Funcția cosinus este abreviată ca cos(x) sau cos(θ) unde x este unghiul în radiani și theta θ este unghiul în grade în general. Funcția cosinus poate fi definită folosind un cerc unitar, adică un cerc cu raza unitară, așa cum vom vedea mai târziu în acest articol. Este periodic în natură și își repetă valorile după fiecare rotație completă a unghiurilor. Pe un plan cartezian, poate fi denumită componenta vectorială a ipotenuzei paralelă cu axa x.

Definiția funcției cosinus

Funcția cosinus este definită într-un triunghi dreptunghic ca raportul dintre lungimea laturii adiacente unghiului în cauză și lungimea ipotenuzei. Matematic Funcția Cosinus este dată ca

Cos x = Cos θ = Lungimea bazei/Lungimea ipotenuzei = b/h = OB/OA

Unde X este unghiul în radiani și θ este unghiul echivalent în grade.

Domeniul și intervalul funcției Cos

Știm că pentru o funcție, domeniul reprezintă valorile de intrare permise, iar intervalul este valoarea de ieșire pentru respectiva intrare sau valoarea de domeniu. Prin urmare, putem presupune că funcția acționează ca un procesor care preia intrare, o procesează și dă o ieșire specială. Domeniul și domeniul funcției cos sunt discutate mai jos:

• Domeniul funcției cosinus: R adică un set de toate numerele reale.
• Intervalul funcției cosinus: [-1, 1], adică ieșirea variază între toate numerele reale între -1 și 1.

Perioada unei funcții cosinus

The funcţie este de natură periodică, adică se repetă după 2π sau 360°. Cu alte cuvinte, se repetă după fiecare rotație completă. Prin urmare, perioada funcției cosinus este o rotație completă sau un unghi de 360° (sau 2π).

Reciprocul unei funcții cosinus

Reciproca unei funcții cosinus este cunoscută ca secantă funcția sau sec pe scurt. Matematic, reciproca funcției cosinus este dată ca

centos vs redhat

sec(θ) = 1/cos(θ)

Conform regulilor de Reciproce , dacă înmulțim Cos x cu Sec x produsul va fi întotdeauna 1.

Graficul funcției cosinus

Graficul funcției cosinus seamănă cu graficul funcției sinus cu o diferență de bază că pentru x = 0 graficul funcției sin trece de la origine, în timp ce la x = 0, graficul funcției cosinus trece de la (0, 1) la y-aixs. Următorul este graficul valorii funcției cosinus, adică y = cos x

Proprietățile discutate mai sus pot fi văzute în grafic ca natura periodică a funcției.

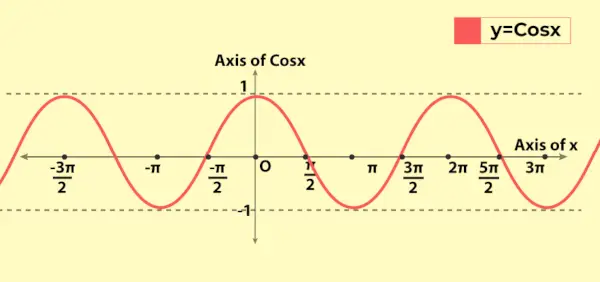
Variația funcției cosinus în grafic

Deoarece intervalul funcției cosinus este [-1, 1], de aceea variază de la -1 la 1 în grafic. Își manifestă natura periodică pe măsură ce graficul se repetă după fiecare lungime 2π pe axa x. Aceasta reflectă faptul că funcția cosinus are o perioadă de 2π (sau 360°).

Cos în Cercul Unității

Funcția cosinus poate fi definită folosind cercul unitar. Să înțelegem cum putem defini funcția cosinus în termeni de cerc unitar.

Considerăm un segment de dreaptă OA care se rotește în jurul punctului O unde O este originea planului cartezian. Astfel, rotația lui OA descrie un cerc unitar (cerc de rază unitară) centrat la originea O și punctul A se află întotdeauna pe acest cerc. Dacă aruncăm o perpendiculară din A pe axa x și numim punctul de intersecție drept B și θ este unghiul pe care OA îl formează cu direcția pozitivă a axei x, atunci cos(θ) = proiecția ipotenuzei pe x -axa = OB/|OA| = OB (deoarece |OA| = 1 unitate).

Rețineți că direcția OB este importantă, așa cum se vede în figurile următoare. Segmentul verde indică lungimea/magnitudinea, iar săgeata indică direcția (+ve sau -ve) cos(θ)

Rețineți că valoarea lui cos(θ) este pozitivă pentru θ aparținând primului și al patrulea cadran, în timp ce negativă pentru θ aparținând celui de-al doilea și al treilea cadran.

Inversa funcției cosinus

Inversa unei funcții cosinus cunoscută ca arc-cosinus funcția și prescurtat ca arccos(x) sau cos ^-1 (X) este definită după cum urmează

cos(x) = y

⇒ cos ^-1 (y) = x

Domeniul și intervalul funcției cosinus invers

Domeniul și domeniul funcției cosinus invers sunt menționate mai jos:

• Domeniul funcției cosinus invers: Toate numerele reale din intervalul [-1, 1]
• Gama funcției cosinus invers: Toate numerele reale din intervalul [0, π]

Funcția cosinus hiperbolic

Funcțiile hiperbolice sunt echivalente analogice ale funcției trigonometrice a cărei expresie algebrică este în termeni de funcție exponențială. Funcția cosinus hiperbolic abreviată ca cosh(x) Unde X este un unghi hiperbolic este un concept de geometrie hiperbolica. La fel ca (cos(x), sin(x)) reprezintă un punct pe un cerc unitar, (cosh(x), sinh(x)) reprezintă un punct pe o hiperbolă unitară, adică xy = 1 unde sinh(x) reprezintă hiperbolic funcția sinus. Expansiunea algebrică a funcției cos hiperbolice este dată ca

cosh(x) = (e ^X + și ^-X )/2

Mai multe detalii despre funcțiile hiperbolice depășesc domeniul de aplicare al acestui articol, dar vă puteți referi la Acest articol .

Funcția cosinus în calcul

Ramura calculului din matematică se ocupă de diferentiere si integrare a unei funcţii date. Diferențierea funcției este rata de schimbare a funcției în raport cu variabila independentă, în timp ce integrarea este procesul invers de diferențiere care se ocupă cu găsirea integralei unei funcții a cărei derivată există.

Derivată a funcției cosinus

The derivat a funcției cosinus este egală cu negativul funcției sinus. Din punct de vedere matematic

d(cos(x))/dx = -sin(x)

Integrarea funcției cosinus

The integrală nedefinită a funcției cosinus este egală cu funcția sinus. Matematic -

∫cos(x)dx = sin(x) + C, unde C este constanta integrării.

Funcții sinus și cosinus

Următorul grafic reprezintă diferența cheie între funcția sinus și cosinus:

Diferența dintre funcțiile sinus și cosinus

Următorul tabel listează diferențele dintre funcția sinus și cosinus -

Tabelul valorilor Cos

Următorul tabel oferă valorile funcției cosinus pentru unele unghiuri comune din primul cadran al planului cartezian -

Putem calcula cu ușurință valorile altor unghiuri comune, cum ar fi 15°, 75°, 195°, -15° etc. folosind aceste valori folosind formulele cos (x + y) și cos (x – y) descrise mai târziu în acest articol. articol.

Verifica, Tabel trigonometric

Identitățile funcției Cos

Identitățile trigonometrice de bază legate de funcția cosinus sunt menționate mai jos:

• fără²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/sec(x)
• cos 2x = cos²x – păcat²x = 1 – 2sin²x = 2cos²x – 1 = (1 – tan²x/1 + tan²X)
• cos 3x = 4cos³x – 3cos x

Articole similare

• Diferențierea funcțiilor trigonometrice
• Funcții trigonometrice inverse
• Derivate Trig inverse

Exemple rezolvate pe funcția cosinus

Iată câteva exemple rezolvate pentru a vă ajuta să înțelegeți mai bine conceptul de funcție cosinus.

Exemplul 1: Care sunt valorile maxime și minime ale funcției cosinus?

Soluţie:

Valoarea maximă a funcției cosinus este 1 la 0° și 180°, în timp ce valoarea minimă a funcției este -1 la 180°.

Exemplul 2: La ce unghi(e) din intervalul [0, 360] este valoarea funcției cosinus 0?

Soluţie:

Valoarea funcției cosinus este 0 la unghiurile de 90° și 270°.

Exemplul 3: Pentru ce cadrane valoarea funcției cosinus este negativă?

Soluţie:

Funcția cosinus este negativă în II^ndși III^rdcadranele.

Exemplul 4: Calculați valoarea cos (45°).

Soluţie:

comanda Linux Run

După identitatea 4 dată mai sus, cos(-x) = cos(x).

Prin urmare, cos(-45°) = cos(45°) = 1/√2

Exemplul 5: Calculați valoarea lui cos(15°).

Soluţie:

Folosind identitatea 3 prezentată mai sus –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Exemplul 6: Ce este cos ^-1 (1/2) în intervalul [0,π]?

Soluţie:

Să cos^-1(1/2) = y.

Prin urmare, cos(y) = 1/2 ⇒ y = π/3 în intervalul dat de mai sus.

Prin urmare, răspunsul este π/3.

Exemplul 7: Care este valoarea lui cos(-15°)?

Soluţie:

Folosind identitatea 3 dată mai sus –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternativ, putem folosi și identitatea cos(-x) = cos(x) și folosim valoarea lui cos(15°) calculată în exemplul 5.

Exemplul 8: Calculați aria de sub graficul funcției cosinus pentru x = 0 până la x = π/2.

Soluţie:

Aria dată poate fi calculată prin rezolvarea următoarei integrale definite –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Prin urmare, răspunsul este 1 unitate pătrat.

Exemplul 9: Dacă cos(x) = π/3, găsiți valoarea lui cos(3x) (în formă zecimală cu precizie de două cifre zecimale).

Soluţie:

Folosind identitatea – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Exemplul 10: Găsiți valoarea lui cos(120°).

Soluţie:

Utilizarea identității pentru cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Întrebări practice: Funcții Cos

Î1. Care este formula pentru a calcula cosul unui unghi dintr-un triunghi dreptunghic?

Q2. Care este interpretarea geometrică a lui cos pe plan cartezian?

Q3. Calculați valoarea lui cos(120°).

Î4. Aflați valoarea lui cos ^-1 (√3/2) în intervalul [π, 2π].

Î5. Dacă un stâlp aruncă o umbră de aceeași lungime pe sol, găsiți unghiul soarelui față de sol dacă soarele este în direcția est.

Rezumat – Funcția cosinus

Funcția cosinus, denumită cos(x), este o funcție trigonometrică fundamentală definită ca raportul dintre bază și ipotenuză într-un triunghi dreptunghic și este esențială în diferite domenii precum fizica, inginerie și geometrie datorită naturii sale periodice. , care este esențial în modelarea comportamentelor undelor. Are un domeniu al tuturor numerelor reale și un interval de la -1 la 1, repetându-și ciclul la fiecare 2 Pi radiani sau 360 de grade, evident din graficul său sub formă de undă care începe la (0,1). Din punct de vedere al calculului, derivata lui cos(x) este − sin( X ), iar integrala ei dă sin( X )+ C , cu C ca constantă a integrării. Această funcție se extinde și la formele hiperbolice, cum ar fi cosh(x), îmbunătățind aplicarea acesteia în diverse contexte și soluții matematice, inclusiv calcule de unde și oscilații în sistemele fizice.

Funcția cosinus: Întrebări frecvente

1. Ce este funcția cosinus?

Funcția cosinus este una dintre funcțiile trigonometrice fundamentale. Este definită într-un triunghi dreptunghic ca raportul dintre lungimea laturii adiacente unghiului în cauză și lungimea ipotenuzei.

2. Cos și cosinus sunt aceleași în trigonometrie?

Da. cos este o abreviere/forma scurtă a funcției cosinus.

3. Care este intervalul funcției Cos?

Intervalul funcției cos sau cosinus este reprezentat de toate numerele reale cuprinse între -1 și 1, adică [-1,1].

4. Ce este funcția Domain of Cos?

Domeniul funcției cos sau cosinus este serul tuturor numerelor reale, adică R .

5. Care este valoarea maximă a funcției cosinus?

Valoarea maximă a funcției cosinus este 1 pentru toate unghiurile echivalente cu 0° sau 360°.

6. Care este valoarea minimă a funcției cosinus?

Valoarea minimă a funcției cosinus este -1 pentru toate unghiurile echivalente cu 180°.

7. Cum să găsiți valoarea lui Cos(-x)?

Valoarea lui cos(-x) poate fi calculată prin calcularea valorii lui cos(x) datorită existenței următoarei identități: cos(-x) = cos(x).

8. Cum se grafică funcția cosinus?

Pentru a desena graficul funcției cosinus pe un plan cartezian, referiți-vă la axa x ca reprezentând unghiuri în radiani (sau grade) și axa y ca reprezentând valorile funcției cosinus pentru unghiul corespunzător pe axa x. Acum,

• Pasul 1: Luați un subset de axa x pentru care doriți să desenați graficul.
• Pasul 2: Împărțiți axa x din acest interval în puncte echidistante (adică există spațiu egal între toate subpunctele). Rețineți, cu cât numărul de diviziuni este mai mare, cu atât este mai mare precizia graficului rezultat.
• Pasul 3: Pentru fiecare dintre aceste subpuncte x, marcați punctul (x, cos(x)) pe grafic.
• Pasul 4: Uniți toate punctele marcate pentru a obține graficul funcției cosinus (pentru submulțimea axei x pe care ați selectat-o).

9. Cum să găsiți perioada unei funcții cosinus?

Perioada unei funcții cosinus se referă la intervalul minim de valori după care funcția începe să se repete. Știm că funcția cosinus se repetă după fiecare rotație completă, ceea ce înseamnă 2π radiani. Prin urmare, perioada funcției cosinus este de 2π radiani sau 360°.

10. Ce este amplitudinea unei funcții cosinus?

Amplitudinea unei funcții cosinus se referă la deplasarea maximă a valorii funcției față de poziția medie, adică axa x. Amplitudinea funcției cosinus este 1, deoarece deplasarea maximă este 1 (pentru valorile -1 și 1 la 180 și respectiv 0 grade. Rețineți că intervalul funcției cosinus este [-amplitudine, amplitudine].