Unghiul se măsoară în grade (°) și radiani. Se formează între cele două laturi adiacente ale unui poligon. Fiecare poligon are laturi diferite și numere diferite de unghiuri. Formula pentru găsirea unghiurilor în grade este utilă în geometrie și trigonometrie. Este esențial să înțelegeți alte concepte ale matematicii, cum ar fi arcul, un unghi central al cercului etc.

1. Un cerc complet = 360°
2. O linie dreaptă = 180°
3. Un semicerc= 180°
4. Un sfert de cerc = 90°

Calcularea unghiurilor în grade

Există trei metode diferite de a găsi unghiuri în grade, care sunt după cum urmează:

1. Folosind protectorul D
2. Folosind teorema lui Pitagora și funcția de trigonometrie într-un triunghi dreptunghic
3. Folosind formula sumei unghiurilor
4. Unghiul central al unui cerc

Folosind protectorul D

Un protector este un tip de riglă sau scară care este folosită pentru a măsura distanța în centimetri sau milimetri. Protectorul utilizat pentru măsurarea unghiurilor este în formă de „D”, cu valoarea unghiurilor marcate de la 0 la 180 ° din orice direcție (dreapta sau stânga). Trebuie să aliniem axa cu linia de pe D pentru a măsura unghiul. Cercul din mijloc al protectorului este aliniat la vârful unghiului de măsurat. Razele de-a lungul vârfului unghiului vor ajuta la găsirea unghiului în grade.

Folosind teorema lui Pitagora și funcția de trigonometrie într-un triunghi dreptunghic

În trigonometrie, există șase funcții, sine, cos, cosec, bronz, cot, și sec. Un triunghi dreptunghic are trei laturi, baza, perpendiculara si ipotenuza.

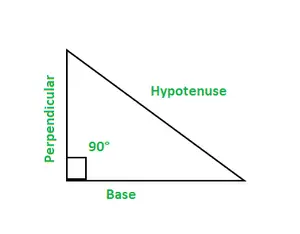
Baza: Este o latură adiacentă unghiului de 90°. Perpendiculară: Este și o latură adiacentă unghiului de 90°.Hipotenuză: Este o latură opusă unghiului de 90°.

Un triunghi dreptunghic este reprezentat printr-un unghi de 90° ca unul dintre unghiuri. Suma totală a unghiurilor unui triunghi este de 180°.

Cosecθ: este reprezentat ca ipotenuză împărțită la perpendiculară.

Cosecθ =

Cotθ: este reprezentată ca bază împărțită la perpendiculară.

Cotθ =

Celelalte funcții trigonometrice sunt reprezentate astfel:

sinθ =

Cosθ =

tanθ =

secθ =

Cosecθ poate fi reprezentat și ca 1/ sinθ

secθ poate fi reprezentat și ca 1/ cosθ

Cotθ poate fi de asemenea reprezentat ca 1/ tanθ

Unde,

Θ este unghiul

Arraylist sortat java

Teorema lui Pitagora

Dacă se cunosc două laturi ale unui unghi drept, putem calcula cu ușurință a treia latură a unui triunghi dreptunghic. Într-un triunghi dreptunghic, teorema lui Pitagora este dată de:

(Ipotenuză)²= (baza)²+ (perpendicular)²

Formula sumei unghiurilor

Suma unghiurilor se referă la suma totală a unghiurilor interne ale unui poligon care se formează între cele două laturi. Dacă există șase laturi ale unui poligon, există în jur de șase unghiuri. Ajută la găsirea unui unghi dacă se cunosc alte unghiuri și suma unghiurilor unui poligon.

Formula pentru a afla suma totală a unghiurilor unui poligon este dată de:

Suma totală a unghiurilor = 180 (n – 2)

Unde,

n este numărul de laturi ale unui poligon

Exemplu:

• Dacă n = 4,

Suma totală a unghiurilor = 180 (4 – 2)

= 180 (2)

= 360°

Dacă n = 5,

Suma totală a unghiurilor = 180 (5 – 2)

= 180 (3)

= 540°

• Dacă n = 6

Suma totală a unghiurilor = 180 (6 – 2)

= 180 (4)

= 720°

Unghiul central al unui cerc

Un cerc este o figură de formă rotundă a cărei graniță este echidistantă de punctul său central. Distanța dintre punctul central și graniță este cunoscută sub numele de raza cercului. Unghiul format de cele două raze ale cercului este cunoscut sub numele de unghi central. Valoarea unghiului central al unui cerc este cuprinsă între 0 și 360 de grade.

Formula de calcul al unghiului central al unui cerc este dată de:

Lungimea arcului = 2πr × (θ/360)

Θ = 360L/2pr

Unde,

r este raza cercului

AB este arcul

Theta este unghiul în grade.

L = lungimea arcului

Exemple de probleme

Întrebarea 1: Aflați unghiul central al unui cerc cu raza de 2m cu o lungime a arcului de 4m?

Soluţie :

Formula de calcul al unghiului central al unui cerc este dată de:

metode în java

Θ = 360L/2pr

Unde,

r este raza cercului

Theta este unghiul în grade.

L = lungimea arcului

Θ = Unghiul în grade

r = 2m

L = 4m

Θ = 360 × 4 /2 × π × 2

Θ = 114,6°

Astfel, unghiul central al cercului este de 114,6°.

Întrebarea 2: Aflați unghiul central al unui cerc cu raza de 10 cm cu o lungime a arcului de 18 cm?

Soluţie :

Formula de calcul al unghiului central al unui cerc este dată de:

Θ = 360L/2pr

Unde,

r este raza cercului

Theta este unghiul în grade.

L = lungimea arcului

r = 10 cm

L = 18 cm

Θ = Unghiul în grade

Θ = 360 × 18 /2 × π × 10

Θ = 103,13°

Astfel, unghiul central al cercului este de 103,13°.

Întrebarea 3: Aflați unghiul unui paralelogram dacă celelalte trei unghiuri sunt de 80°, 95° și 105°?

Soluţie :

Există patru laturi într-un paralelogram cu suma totală a unghiurilor 360°.

Formula pentru a afla suma unghiurilor = 180 (n – 2)

Unde,

n este numărul de laturi ale unui poligon

Aici, n = 4,

Suma totală a unghiurilor = 180 (4 – 2)

= 180 (2)

tastatură pagina în jos

= 360°

Suma totală = Unghiul 1 + Unghiul 2 + Unghiul 3 + Unghiul 4

360 = 80+ 95+ 105+ Unghiul 4

360 = 280 + Unghiul 4

Unghiul 4 = 360 – 280

Unghiul 4 = 80°

Întrebarea 4: Găsiți unghiul A în figura dată.

Soluţie :

Dat: Hipotenuza = 12

Perpendiculară = 6

Funcția de trigonometrie pentru calcularea unghiului este dată de:

sinA = 6/12

A = 30°

Întrebarea 5: Găsiți unghiul A în figura dată.

Soluţie :

Dat: Hipotenuza = 10

Baza = 5

Funcția de trigonometrie pentru calcularea unghiului este dată de:

CosA = 5/10

A = 60°

Întrebarea 6: Aflați unghiul unui pentagon dacă alte patru unghiuri sunt 115°, 100°, 105° și 100°?

Soluţie :

Există cinci laturi într-un pentagon cu suma totală a unghiurilor 540°.

Formula pentru a afla suma unghiurilor = 180 (n – 2)

constructor în java

Unde,

n este numărul de laturi ale unui poligon

Aici, n = 5,

Suma totală a unghiurilor = 180 (5 – 2)

= 180 (3)

= 540°

Suma totală = Unghiul 1 + Unghiul 2 + Unghiul 3 + Unghiul 4 + Unghiul 5

540 = 115° + 100° + 105°+100° + Unghiul 5

540 = 420 + Unghiul 5

Unghiul 5 = 540 – 420

Unghiul 5 = 120°

Întrebarea 7: Găsiți unghiul A în figura dată.

Soluţie :

Dat: Baza = √3

Perpendiculara = 1

Funcția de trigonometrie pentru calcularea unghiului este dată de:

tanθ =

tanθ = 1/√3

A = 30°

Întrebarea 8: Aflați unghiul unui paralelogram dacă celelalte trei unghiuri sunt de 100°, 70° și 80°?

Soluţie :

Există patru laturi într-un paralelogram cu suma totală a unghiurilor 360°.

scrieți json în fișierul python

Formula pentru a afla suma unghiurilor = 180 (n – 2)

Unde,

n este numărul de laturi ale unui poligon

Aici, n = 4,

Suma totală a unghiurilor = 180 (4 – 2)

= 180 (2)

= 360°

Suma totală = Unghiul 1 + Unghiul 2 + Unghiul 3 + Unghiul 4

360 = 100 + 70 + 80 + Unghiul 4

360 = 250 + Unghiul 4

Unghiul 4 = 360 – 250

Unghiul 4 = 110°

Astfel, celălalt unghi este de 110°.

Întrebarea 9: Aflați unghiul unui hexagon dacă alte cinci unghiuri sunt 120°, 115°, 110°, 125° și 105°?

Soluţie :

Există șase laturi într-un hexagon cu suma totală a unghiurilor 720°.

Formula pentru a afla suma unghiurilor = 180 (6 – 2)

Unde,

n este numărul de laturi ale unui poligon

Aici, n = 6,

Suma totală a unghiurilor = 180 (6 – 2)

= 180 (4)

= 720°

Suma totală = Unghiul 1 + Unghiul 2 + Unghiul 3 + Unghiul 4 + Unghiul 5 + Unghiul 6

720 = 120 + 115 + 110 + 125 + 105 + Unghiul 6

720 = 575 + Unghiul 6

Unghiul 6 = 720 – 575

Unghiul 6 = 145°

Astfel, al șaselea unghi al hexagonului este de 145°.