Cercul unitar este un cerc a cărui rază este 1. Centrul cercului unitar este la originea (0,0) pe axă. The circumferinţă a cercului unității este de 2 π unități, în timp ce aria cercului unității este de π unități2. Poartă toate proprietățile lui Circle. Cercul unitar are ecuația x2+ și2= 1. Acest cerc de unitate ajută la definirea diferitelor concepte trigonometrice.
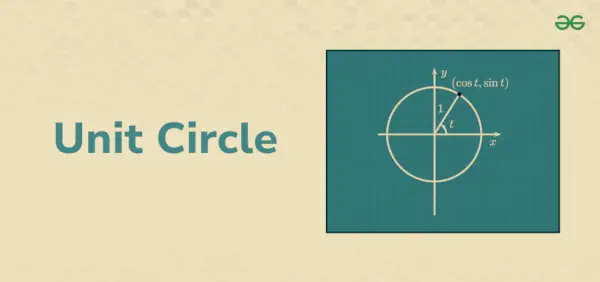
Cercul de unitate
Cercul unității este adesea notat ca S1generalizarea la dimensiuni mai mari este sfera unitară. Să înțelegem mai multe despre unitatea de cerc, formulă și exemplele rezolvate în detaliu mai jos.
Ce este Unit Circle?
Cercul unitar este un cerc care are o rază de una (1) unitate. Folosim planul cartezian pentru a desena un cerc unitar, iar un cerc unitar este un polinom de 2 grade cu două variabile. Cercul unitar are diverse aplicații în trigonometrie și algebră și este utilizat în principal pentru a găsi valorile diferitelor rapoarte trigonometrice, cum ar fi sin x, cos x, tan x și altele.
Definiția cercului unității
În matematică, definim un cerc unitar drept locul unui punct fix care se află la o distanță de o unitate de centrul cercului. Un cerc unitar are o rază de o unitate și de aici denumirea de cerc unitate.
Ecuația cercului unitar
Știm că ecuația oricărui cerc cu centrul (h, k) și raza „r” este,
(x – h) 2 + (y – k) 2 = r 2
Pentru un cerc unitar știm că r este 1 unitate și deci ecuația cercului unitar este,
(x – h) 2 + (y – k) 2 = 1
Formula cercului unitar
Dacă centrul cercului unitar este originea, adică (h, k) = (0, 0), atunci ecuația cercului unitar este,
X 2 + și 2 = 1
Un cerc unitar este reprezentat în imaginea adăugată mai jos, cu coordonatele centrului h, k iar când cercul este la origine valoarea lui h și k este zero și raza AP este egală cu 1 unitate.
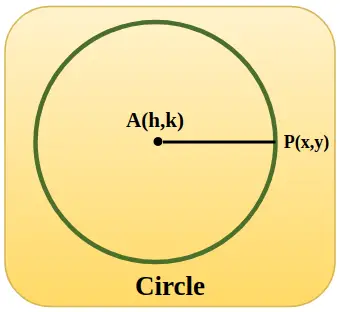
Funcții trigonometrice folosind cercul unitar
Aplicarea teoremei lui Pitagora într-un cerc unitar poate fi folosită mai bine pentru a înțelege funcțiile trigonometrice. Pentru aceasta, considerăm că un triunghi dreptunghic este plasat în interiorul unui cerc unitar în planul de coordonate carteziene. Dacă observăm, raza acestui cerc denotă ipotenuza triunghiului dreptunghic.
Raza cercului formează un vector. Aceasta duce la formarea unui unghi, să spunem θ cu axa x pozitivă. Să presupunem că x este lungimea bazei și, respectiv, lungimea altitudinii triunghiului dreptunghic. De asemenea, coordonatele punctelor finale ale vectorului rază sunt (x, y), respectiv.
Triunghiul dreptunghic deține laturile 1, x și respectiv y. Raportul trigonometric poate fi calculat acum, după cum urmează:
sin θ = Altitudine/Hipotenuză = y/1
cos θ = Baza/Hipotenuza = x/1
Acum,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Prin înlocuirea valorilor lui θ, putem obține valorile principale ale tuturor funcțiilor trigonometrice. Se găsesc valori similare ale funcțiilor trigonometrice la diferite valori.
Unit Circle cu Sin Cos și Tan
Orice punct al cercului unitar cu coordonatele (x, y) este reprezentat folosind identitati trigonometrice ca, (cosθ, sinθ). Coordonatele colțurilor razei reprezintă cosinusul și sinusul valorilor θ pentru o anumită valoare a lui θ și linia razei. Avem cos θ = x și sin θ = y. Există patru părți ale unui cerc fiecare situată într-un cadran, formând un unghi de 90°, 180°, 270° și 360°. Valorile razei se situează între -1 și respectiv 1. De asemenea, valorile sin θ și cos θ se află între 1 și respectiv -1.
Cercul unității și identitățile trigonometrice
Identitățile trigonometrice ale cercului unitar pentru cotangentă, secantă și cosecantă pot fi calculate folosind identitățile pentru sin, cos și tan. În mod concludent, obținem un triunghi dreptunghic cu laturile 1, x și respectiv y. Calcularea identităților cercului unitar poate fi exprimată ca,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sec θ = 1/x
- cosec θ = 1/y
- cot θ = x/y
Diagrama cercului unității
Diagrama cercului unitar este o diagramă care conține valoarea funcției trigonometrice sinus și cosinus pentru diferite unghiuri. Diagrama cercului unității pentru aceeași este adăugată mai jos,
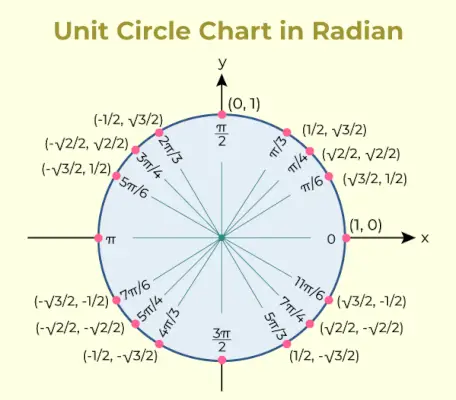
Masa cercului unității
Rapoartele trigonometrice utilizate în tabelul cercului unitar sunt folosite pentru a enumera coordonatele punctelor din cercul unității care corespund unghiurilor comune.
arbore avl
| Unghiuri | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| fără | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| asa de bash dacă altceva | 0 | 1/√(3) | 1 | √(3) | Nedefinit |
| csc | Nedefinit | 2 | √(2) | 23) | 1 |
| sec | 1 | 23) | √(2) | 2 | Nedefinit |
| pat | Nedefinit | √(3) | 1 | 1/√(3) | 0 |
Cercul unității Identități pitagoreice
Există trei identități pitagorice și toate sunt ușor de demonstrat folosind conceptul de cerc unitar cele trei identități pitagoreice sunt,
- fără2θ + cos2θ = 1
- 1 + deci2θ = sec2i
- 1 + patut2θ = cosec2i
Unitate Cerc Plan complex
Numere complexe și Planul complex sunt ușor de explicat folosind conceptul de cerc unitar. Ecuația cercului unitar în formă complexă este,
|z| = 1
SAU
X 2 + și 2 = 1
În forma lui Euler, numărul complex este reprezentat ca:
z = e aceasta = cos t + i(sin t)
Citeşte mai mult
Exemple rezolvate pe cercul unității
Q1: Demonstrați că punctul Q se află pe un cerc unitar, Q = [1/√(6), √4/√6]
Soluţie:
Dat,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Ecuația cercului unitar este,
X2+ și2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Astfel, punctul Q[1/√(6), √4/√6] nu se află pe cercul unitar.
Î2: Calculați astfel 30 O folosind valorile sin și cos ale cercului unitar.
Soluţie:
tan 30° folosind valorile sin și cos,
cea mai buna masina din lumetan 30° = (sin 30°)/ (cos 30°)
- fără 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
tan 30° = 1/√(3)
Q3: Validați dacă punctul P [1/2, √(3)/2] se află pe cercul unitar.
Soluţie:
Dat,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Ecuația cercului unitar este,
- X2+ și2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Întrebări practice pe Cercul unității
Î1. Verificați dacă punctele A (1/2, 3/2) se află pe un cerc unitar.
Q2. Verificați dacă punctele A (2, 1/2) se află pe un cerc unitar.
Q3. Aflați valoarea cos 240°
Î4. Aflați valoarea tan 320°
Î5. Aflați valoarea sin 160°
Unit Circle – Întrebări frecvente
Ce este Unit Circle?
Un cerc unitar este definit ca locația unui punct la o unitate distanță de un punct fix. Are un centru la (0,0) și valoarea razei sale este 1.
Cum se verifică dacă un punct se află pe cercul unității?
Orice punct situat într-un plan 2D care are forma (x, y) este pus în ecuația cercului unitar x2+ și2= 1 pentru a verifica dacă se află sau nu pe cerc.
Care este formula cercului unitar?
Formula cercului unitar este o formulă care este utilizată pentru a reprezenta algebric un cerc unitar. Formula cercului unitar este dată ca:
X 2 + și 2 = 1
De ce se numește Unit Circle?
Un cerc unitar se numește cerc unitar deoarece are o rază de una (1) unități.
