Rădăcina pătrată a lui 3 este un număr real pozitiv care va da numărul 3 atunci când este înmulțit cu el însuși. Rădăcina pătrată a lui 3 este un număr irațional, deoarece este o zecimală care nu se încheie și nu se repetă. Rădăcina pătrată a lui 3 se notează ca √3 sau 31/2. Deoarece pătratul lui 3 este un număr irațional, valoarea sa zecimală exactă nu este niciodată calculată.
Valoarea rădăcinii pătrate a lui 3, √3 =1,732 (trunchiată)
În acest articol, vom afla în detaliu despre rădăcina pătrată a lui 3.
Cuprins
- Ce este rădăcina pătrată a lui 3?
- Valoarea rădăcină 3 în matematică
- Rădăcina pătrată a lui 3 este rațională sau irațională?
- Cum să găsești rădăcina pătrată a lui 3?
- Proprietățile rădăcinii pătrate a unui număr
- Tabelul rădăcinii pătrate
Ce este rădăcina pătrată a lui 3?
Rădăcina pătrată a unui număr este un număr care, înmulțit cu el însuși, are ca rezultat numărul inițial.
Exemplu: Rădăcina pătrată a lui 16 este 4, deoarece 4×4 = 16 deci √16 = 4
șir comparabil
Rădăcina pătrată a lui 3 sau pur și simplu numită rădăcină 3 este un număr irațional care prin înmulțirea cu el însuși are ca rezultat numărul 3. Putem da valoarea aproximativă a rădăcinii 3 ca:
- Forma zecimală: 1,732
- Forma exponentului: 31/2
- Forma radicală: √3
Valoarea rădăcină 3 în matematică
În matematică, găsirea rădăcinii pătrate a oricărui număr este foarte importantă, rădăcina pătrată a pătratului perfect poate fi calculată cu ușurință. Pentru pătratele imperfecte, găsirea unei rădăcini pătrate este dificilă și se calculează în general folosind metoda diviziunii lungi.
Rădăcina lui 3 este exprimată ca √3, este un număr irațional, astfel încât valoarea sa zecimală nu poate fi niciodată calculată. Este reprezentat sub forma radicală ca (3)½. Rădăcina pătrată a lui 3 rotunjită la 7 zecimale este 1,7320508.
a spus Madhuri haide
Rădăcina pătrată a lui 3 = 1,7320508075688772…
Rădăcina pătrată a lui 3 este rațională sau irațională?
Rădăcina pătrată 3 este o zecimală neterminabilă și nerepetabilă și toate zecimale care nu se încheie și nerepetă sunt sub număr irațional. Deci, este sigur să spunem că √3 este an număr irațional .
Expansiunea zecimală a rădăcinii pătrate a lui 3 este,
√3 = 1,7320508075688772…
salut lumea java
Deoarece nu se repetă și nu se încheie, putem spune cu siguranță √3 este irațional.
Cum să găsești rădăcina pătrată a lui 3?
Este întotdeauna mai ușor să calculăm rădăcina pătrată a pătratelor perfecte, dar pentru a calcula rădăcina pătrată a unui pătrat neperfect, trebuie să efectuăm metoda diviziunii lungi.
Pentru a calcula rădăcina pătrată a lui 3, trebuie să urmam pașii de mai jos:
Pasul 1: Scrieți 3 ca 3,000000 (unde zerourile sunt întotdeauna păstrate sub formă de perechi) pentru a facilita împărțirea.
Pasul 2: Acum căutați pătratul perfect mai mic decât 3, adică 1, și împărțiți numărul cu el.
Pasul 3: Acum, câtul este 1, iar restul este 2. Vom plasa o zecimală în cât și vom reduce perechea de zerouri pentru o împărțire ulterioară.
Pasul 4: Acum, următorul dividend este 200, adăugați următorul divizor va fi 2X (coantul 1 se adaugă la divizorul anterior 1 și X este pe locul al zecelea), astfel încât înmulțirea numărului 2X și X ar trebui să fie mai mică de 200. Acest lucru va da următoarea valoare 27 ca noul divizor.
Pasul 5: Acum 7 se adaugă la cot după o zecimală, deci valoarea coeficientului va fi 1,7 iar noul divizor se va obține prin adăugarea de la 7 la 27, deci 34Y, unde Y se află pe locul sute. Folosind pașii anteriori, putem continua și vom obține rădăcina pătrată a lui 3 în coeficient.
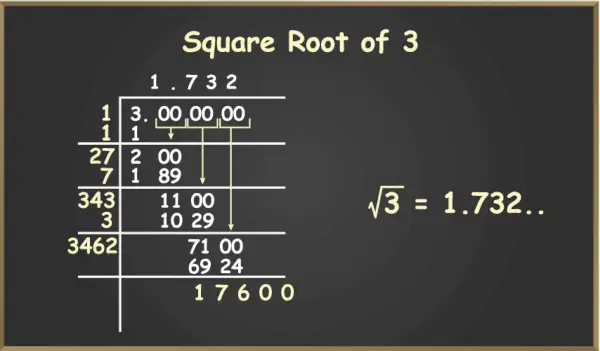
Rădăcina pătrată a lui 3
Acum aduceți în jos următoarea pereche de zerouri și repetați pașii 4 și 5. Acest lucru se poate face pentru pași infiniti, deoarece valoarea exactă a rădăcinii pătrate a lui 2 merge până la infinite zecimale. Putem calcula rezultatul cu până la 4 zecimale, deoarece acesta poate fi folosit pentru aprox. valoarea rădăcinii pătrate.
Proprietățile rădăcinii pătrate a unui număr
Diferite proprietăți ale rădăcinii pătrate a unui număr sunt discutate mai jos,
identificatori validi în java
- Numerele pătrate perfecte au rădăcini pătrate perfecte.
- Rădăcina pătrată a unui pătrat chiar perfect este pare.
- Rădăcina pătrată a unui pătrat perfect impar este impară.
- Rădăcina pătrată a unui număr negativ este a număr complex .
Tabelul rădăcinii pătrate
Rădăcinile pătrate ale diferitelor numere sunt utilizate pe scară largă în matematică. Tabelul de mai jos ne oferă rădăcina pătrată a diferitelor numere care sunt utilizate în mod obișnuit.
| Număr | Rădăcină pătrată |
|---|---|
| 1 | √(1) = 1 |
| 2 | √(2) = 1,414 (aproximativ) |
| 3 | √(3) = 1,732 (aproximativ) |
| 4 | √(4) = 2 |
| 5 | √(5) = 2,236(aproximativ) |
| 9 | √(9) = 3 |
| 16 | √(16) = 4 |
| 25 | √(25) = 5 |
De asemenea, verifica
- Rădăcina pătrată a lui 2
- Numere reale
- Numere rationale
Întrebări frecvente despre rădăcina pătrată a lui 3
Care este valoarea rădăcinii pătrate a lui 3?
Valoarea aproximativă a rădăcinii pătrate a lui 3 este 1,73205.
ce este un personaj special
De ce rădăcina pătrată a lui 3 este un număr irațional?
Valoarea rădăcinii pătrate a lui 3 este o zecimală care nu se repetă și nu se încheie, deci este un număr irațional.
Numărul 3 este un pătrat perfect?
3 este un număr prim și numerele prime nu au alți factori decât 1 și ele însele. Astfel, putem spune că 3 nu este un pătrat perfect.
Cum putem găsi valoarea lui √3?
Valoarea lui √3 poate fi găsită folosind metoda diviziunii lungi. Deoarece 3 nu este un pătrat perfect, valoarea lui exactă nu este niciodată găsită.
Care este valoarea rădăcinii 2?
Rădăcina 2 este un număr irațional, astfel încât valoarea sa zecimală exactă nu este niciodată găsită. Valoarea aproximativă a rădăcinii 2 este, √2 = 1,414 (aproximativ)
