Dobânda compusă este dobânda care este calculată pentru suma unui împrumut sau depozit în care se calculează dobânda pentru principal, precum și pentru dobânda câștigată anterior.

Diferența comună dintre dobânda compusă și cea simplă este aceea că în interes compus , dobânda este calculată pentru suma principală, precum și pentru dobânda câștigată anterior, în timp ce dobânda simplă depinde doar de principalul investit.

Cuprins

• Ce este dobânda compusă?
• Formula dobânzii compuse
• Cum se calculează dobânda compusă?
• Formula dobânzii compuse – Derivare
• Formula semestrială a dobânzii compuse
• Formula trimestrială a dobânzii compuse
• Formula lunară a dobânzii compuse
• Formula zilnică a dobânzii compuse
• Formula Ratei de Compunere Periodică
• Regula 72
• Dobânda compusă de ani consecutivi
• Formula dobânzii compuse continue
• Alte aplicații de interes compus
• Diferența dintre dobânda compusă și dobânda simplă
• Exemple de interes compus
• Interes compus – Întrebări practice

Ce este dobânda compusă?

Dobânda compusă este dobânda pentru suma principală, precum și dobânda câștigată pentru suma principală. Cuvântul interes compus este compus din două cuvinte Compus care înseamnă compus din două sau mai multe și Dobândă înseamnă bani câștigați la împrumutul sumei. Prin urmare, dobânda compusă este banii câștigați din împrumuturi și este compusă din două tipuri de dobânzi care sunt:

• Dobândă la suma principală

• Dobândă la dobânda câștigată la valoarea principalului de-a lungul perioadei

Definiția dobânzii compuse

Interes compus este dobânda calculată pe principal și dobânda câștigată anterior. Este notat cu C.I. Este foarte util pentru investiții și rambursarea împrumutului. Este cunoscut și sub denumirea de dobândă pe dobândă.

sincronizare java

Interes compus este foarte util în sectoarele bancar și financiar și este util și în alte sectoare. Câteva dintre utilizările sale sunt:

• Creșterea populației unei țări
• Valoarea investiției pe o perioadă de timp.
• Pentru găsirea costurilor umflate și a valorii amortizate a oricărui articol.
• Pentru prezicerea creșterii oricărei instituții sau țări.

Dobândă compusă (C.I) = Sumă – Principal

Formula dobânzii compuse

Interes compus se calculează, după calcularea sumei totale pe o perioadă de timp, pe baza ratei dobânzii, și a principalului inițial. Pentru un principal inițial de P, rata dobânzii pe an de r, perioada de timp t în ani, frecvența de câte ori dobânda este compusă anual n, formula de calcul a CI este următoarea:

CI = P(1 + r/100) ⁿ – P

Formula de mai sus pentru calcularea dobânzii compuse este adăugată în imaginea de mai jos:

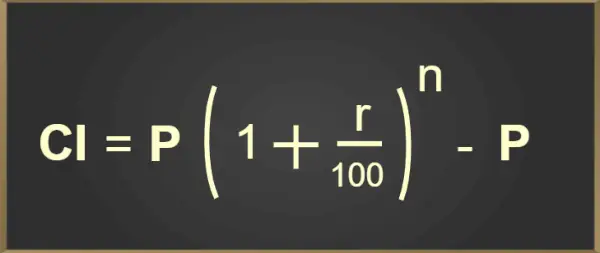
Formula dobânzii compuse

Unde,

• P = Principal
• r = Rata dobânzii
• n = Numărul de ocazii în care dobânda este compusă pe an
• t = Timp (în ani)

Putem scrie formula pentru dobânda compusă ca:

Dobândă compusă = A – P

Unde,

• A = Suma totală de bani după compunere
• P = Suma principală inițială

Dobândă compusă = P(1 + r/n) ^nt -P

Unde,

• P = Suma principală inițială
• r = Rata anuală a dobânzii
• n = Numărul de cazuri în care dobânda este compusă
• t = Numărul de ani

Dobânda compusă poate fi calculată anual, semestrial, trimestrial, lunar, zilnic etc. conform cerințelor.

Cum se calculează dobânda compusă?

Interes compus este dobânda plătită atât pentru principal, cât și pentru dobânda acumulată. Dobânda câștigată la fiecare interval se adaugă la principalul inițial și astfel principalul continuă să crească.

Utilizați următoarele metode pentru a găsi dobânda compusă.

Pasul 1: Notă, principal, rata și perioada de timp date

Pasul 2: Calculați suma folosind formula A = P(1 + r/100) ⁿ

Pasul 3: Găsiți dobânda compusă folosind formula CI = Sumă – Principal

La intervale regulate, dobânda acumulată până acum este asociată cu suma principală existentă și apoi dobânda este calculat pentru noul principal . Noul principal este egal cu suma principalului inițial și a dobânzii acumulate până acum.

Dobândă compusă = Dobândă pe principal + Dobândă pe dobândă principal (din al doilea an și după aceea)

Dobânda compusă este calculată la intervale regulate, cum ar fi anual (anual), semestrial, trimestrial, lunar, etc; Este ca și cum, reinvestirea veniturilor din dobânzi dintr-o investiție face ca banii să crească mai repede în timp! Este exact ceea ce dobânda compusă face banilor. Băncile sau orice organizație financiară calculează suma numai pe baza dobânzii compuse.

Formula dobânzii compuse – Derivare

Formula dobânzii compuse este un instrument puternic utilizat în finanțe pentru a calcula dobânda câștigată sau plătită pe o sumă principală inițială, care include atât principalul inițial, cât și dobânda acumulată în perioadele precedente. Formula dobânzii compuse este dată de:

Unde,

• A este valoarea viitoare a investiției sau a împrumutului, inclusiv dobânda
• P este suma principală (investiția inițială sau suma împrumutului)
• r este rata anuală a dobânzii (sub formă zecimală)
• n este numărul de ori în care dobânda este compusă pe an
• este timpul pentru care banii sunt investiți sau împrumuți, în ani

Formula simplă a dobânzii

Dobânda simplă se calculează numai pe suma principală. Poate fi reprezentat prin formula ,

Formula dobânzii compuse cu amestecare continuă

Atunci când dobânda este compusă în mod continuu (de nenumărate ori pe an), formula pentru dobânda compusă este derivată folosind formula pentru combinare continuă:

Unde,

• e este numărul lui Euler (aproximativ 2,71828)
• P este suma principală
• r este rata anuală a dobânzii
• t este Timpul în ani

Formula generală a dobânzii compuse

Pentru a obține formula generală a dobânzii compuse, să luăm în considerare cumularea dobânzii de n ori pe an.

Dacă P este compus de n ori pe an la o rată anuală a dobânzii r, dobânda r este împărțită la n și se aplică de n ori pe an. Deci, după t ani, formula devine:

funcție anonimă java

Unde,

• reprezintă rata dobânzii pe perioadă de capitalizare.
• nt este numărul total de perioade de capitalizare pe t ani.

Acest formula ilustrează modul în care suma inițială a principalului crește în timp atunci când dobânda este compusă la intervale regulate . Pe măsură ce n se apropie de infinit (adică, compunerea continuă), formula converge către formula de amestecare continuă .

În concluzie, formula dobânzii compuse este un rezultat al formulei de amestecare continuă adaptată pentru perioade de amestecare discrete pe an. Permite calcularea valorii viitoare a unei investiții sau a unui împrumut, luând în considerare dobânda compusă la intervale regulate.

Formula semestrială a dobânzii compuse

Fie principalul investit P și rata dobânzii este R % pe an, care este compusă semestrial timp de „t” ani

La fel de se combină semestrial, principalul va fi modificat la sfârșitul a 6 luni, iar dobânda câștigată până atunci va fi adăugată la principal și apoi acesta devine noul principal. În mod similar, se calculează suma finală.

Noi stim,

rata = R% pe an, compus semestrial

rata = (R/2) %

timpul este de t ani știm că t ani au 2t jumătate de ani.

Acum,

A = P (1 + R/200) ^2t

CI = A – P

Formula trimestrială a dobânzii compuse

Fie principalul investit P și rata dobânzii este R % pe an, care este compusă trimestrial timp de t ani.

La fel de este compus trimestrial, principalul va fi modificat la sfârșitul a 3 luni, și dobânda câștigată până atunci va fi adăugată la principal și apoi acesta devine noul principal. În mod similar, se calculează suma finală.

noi stim,

rata = R% pe an compusă trimestrial

rata = (R/4)%

timpul este de t ani știm că t ani au 4t sferturi.

Acum,

A = P(1 + R/400) ^4t

CI = A – P

Verifica: Formula trimestrială a dobânzii compuse

Formula lunară a dobânzii compuse

Dacă dobânda este compusă lunar, atunci numărul de ori de compus va fi de 12, iar dobânda în fiecare lună va fi 1/12 din dobânda compusă anuală. Prin urmare, Formula de dobândă compusă lunară este dată ca

A = P[1 + (R/1200)] ^12t

CI = A – P

Verifica: Formula lunară a dobânzii compuse

Formula zilnică a dobânzii compuse

Dacă dobânda este compusă zilnic, atunci.

Noua rată a dobânzii va fi R/365 %

n = 365

Prin urmare, Formula zilnică a dobânzii compuse este dată ca:

A = P[1 + (R/36500)] ^365t

CI = A – P

Formula Ratei de Compunere Periodică

Suma totală, inclusiv principalul P și dobânda compusă CI, este dată de:

A = P[1 + (r/n)] ^nt

Unde,

• P = Principal
• A = Suma finală
• r = Rata anuală a dobânzii
• n = Numărul de cazuri în care dobânda este agravată
• t = Timp (în ani)

Astfel, dobânda compusă este:

CI = A – P

Regula 72

Regula lui 72 este formula care este folosită pentru a estima câți ani banii noștri se dublează dacă sunt cumulați anual. Pentru exemplu , dacă banii noștri sunt investiți la r % compus anual, apoi este nevoie de 72/r ani pentru ca banii noștri să se dubleze.

Acest calcul este util și pentru a calcula valoarea umflată a banilor noștri, adică arată în câți ani valoarea activului nostru se reduce la jumătate dacă este amortizat anual.

Formula regulii 72

Următoarea formulă este utilizată pentru a aproxima numărul de ani pentru ca investiția noastră să se dubleze.

N = 72/r

Unde,

• N este numărul aproximativ al anului, banii noștri se dublează
• r este rata la care banii noștri sunt calculati anual

Exemplu cu regula 72

Să presupunem că Kabir a investit 10.00.000 de rupii într-un fond de datorii care oferă o rentabilitate de 8%. Aflați în câți ani banii săi se dublează dacă sunt cumulați anual.

Folosind formula de mai sus: N = 72/8 = 9 ani

Prin urmare, este nevoie de 9 ani pentru ca banii lui Kabir să se dubleze.

Dobânda compusă de ani consecutivi

Dacă avem aceeași sumă și aceeași rată a dobânzii. C.I. al unui anumit an este întotdeauna mai mult decât C.I al anului precedent. (IC al 3-lea an este mai mare decât IC al 2-lea an). Diferența dintre CI pentru oricare doi ani consecutivi este dobânda de un an la C.I din anul precedent.

C.I de anul 3 – C.I de anul 2 = C.I de anul 2 × r × 1/100

Diferența dintre sumele oricărui doi ani consecutivi este dobânda de un an pe suma anului precedent.

Suma anului 3 – Suma anului 2 = Suma anului 2 × r × 1/100

Rezultate cheie

Când avem aceeași sumă și aceeași rată ,

C.I pentru al n-lea an = C.I pentru (n – 1) an + Dobândă pentru un an la C.I pentru (n – 1) an

Formula dobânzii compuse continue

Formula de amestecare continuă este utilizată în Finanțe pentru a calcula valoarea finală a unei investiții care suferă o combinare continuă pe o perioadă diferită și valoarea este adăugată în timp. Formula pentru compunerea continuă este dată ca

Valoarea finală = Valoarea prezentă × e ^rt

Unde,

• r este rata dobânzii
• este timpul

Află mai multe, Formula de amestecare continuă

Alte aplicații de interes compus

Creştere: Acesta este utilizat în principal pentru creștere dacă industriile sunt legate.

Producția după n ani = producția inițială × (1 + r/100) ⁿ

Amortizare: Când costul unui produs se depreciază cu r% în fiecare an, atunci valoarea acestuia după n ani este

Valoarea actuală × (1 + r/100) ⁿ

Probleme ale populației: Când populația unui oraș, oraș sau sat crește într-un anumit ritm pe an.

conversia șirului în dată

Populația după n ani = populația actuală × (1 + r/100) ⁿ

Diferența dintre dobânda compusă și dobânda simplă

Diferența dintre dobânda compusă și dobânda simplă poate fi învățată mai jos în acest articol

Exemple de interes compus

Câteva exemple de formule ale dobânzii compuse sunt:

Exemplul 1: Găsiți dobânda compusă când principalul = 6000 Rs, rata = 10% pe an și timpul = 2 ani.

Soluţie:

Dobândă pentru primul an = (6000 × 10 × 1)/100 = 600

Suma la sfârșitul primului an = 6000 + 600 = 6600

Dobândă pentru al doilea an = (6600 × 10 × 1) / 100 = 660

Suma la sfârșitul celui de-al doilea an = 6600 + 660 = 7260

Dobândă compusă = 7260 – 6000 = 1260

Exemplul 2: Care va fi dobânda compusă pentru 8000 Rs în doi ani, când rata dobânzii este de 2% pe an?

Soluţie:

Dat,

• P principal = 8000
• Rata r = 2%
• Timp = 2 ani

prin formula

A = P (1 + R/100) ⁿ

A = 8000 (1 + 2/100)²= 8000 (102/100)²

A = 8323

Dobânda compusă = A – P = 8323 – 8000 = 323 Rs

Exemplul 3: Hari a depus Rs. 4000 cu o societate financiară timp de 2 ani la o dobândă de 5% pe an. Care este dobânda compusă pe care o primește Rohit după 2 ani?

Soluţie:

Dat,

• P principal = 4000
• Rata r = 5%
• Timp = 2 ani

Prin formula,

A = P (1 + R/100)ⁿ

A= 4000 (1 + 5/100)²

A= 4000 (105/100)²

A= 4410

Dobândă compusă = A – P = 4410 – 4000 = 410

Exemplul 4: Găsiți dobânda compusă pe Rs. 2000 cu o rată de 4 % pe an timp de 1,5 ani. Când dobânda este compusă semestrial?

Soluţie:

parametrul verilog

Dat,

• p principal = 2000
• Rata r = 4%
• Timp = 1,5 (adică 3 jumătate de ani)

prin formula,

A = P (1 + R/200) ²ⁿ

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

A = 2122

Dobândă compusă = A – P = 2122 – 2000 = 122

Exemplul 5: Care este dobânda compusă pentru 10000 timp de un an la o rată de 20% pe an, dacă dobânda este compusă trimestrial?

Soluţie:

Dat,

• Principal P = Rs 10000
• Rata R = 12% (12/4 = 3% pe trimestru de an)
• Timp = 1 an (1 × 4 = 4 trimestre)

După formulă,

A = P (1 + R/100) ⁿ

A = 10000 (1 + 3/100) ⁴

A = 10000 (103/100) ⁴

A = 11255

Dobândă compusă = A – P = 11255 – 10000 = 1255

Exemplul 6: Găsiți dobânda compusă la o rată de 5% pe an timp de 2 ani asupra acelui principal care în 2 ani la rata de 5% pe an dat Rs. 400 ca dobanda simpla.

Soluţie:

Dat,

• Dobândă simplă IF = 400
• Rata R = 5%
• Timp T = 2 ani

După formulă,

Dobândă simplă = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Rata dobânzii compuse = 5%

P = 40000/10 = 4000 Rs

Timp = 2 ani

După formulă,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

A = 4410

Dobândă compusă = A – P = 4410 – 4000 = 410

industrie și fabrică

Exemplul 7: Găsiți dobânda compusă pentru 30000 Rs la 7% dobândă compusă anual timp de doi ani.

Soluţie:

• P principal = 30000 Rs
• Rata R = 7%
• Timp = 2 ani

Prin formula,

A = P (1 + R/100) ⁿ

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

A = 34347

Dobândă compusă = A – P = 34347 – 30000 = 4347

Lecturi similare:

• Dobânda compusă zilnică
• Dobândă lunară compusă
• Soluție de dobândă compusă clasa 8
• Interes compus – Întrebări și răspunsuri de aptitudini
• Interes simplu

Interes compus – Întrebări practice

Diverse întrebări practice privind interesele compuse sunt:

Î1. Găsiți suma care trebuie plătită după 3 ani dacă se împrumută o sumă de 10000 la rata de 4% compusă anual.

Q2. Găsiți dobânda care trebuie plătită după 1,5 ani dacă o sumă de 2500 este împrumutată la o rată de 6% compusă semestrial.

Q3. Calculați dobânda compusă pentru o sumă de 9000 împrumutată la rata de 5% trimestrial timp de 15 luni.

Î4. Calculați dobânda compusă pentru o sumă de 20000 împrumutată la rata de 12% timp de 3 luni compusă lunar

Încheierea dobânzii compuse

Dobânda compusă este a concept financiar puternic care permite investițiilor sau împrumuturilor să crească sau să se acumuleze în timp. Spre deosebire de dobânda simplă, care calculează doar dobânda la suma principală inițială, interes compus ia în considerare dobânda câștigată atât pentru principalul inițial, cât și pentru orice dobândă acumulată din perioadele anterioare.

Interes compus – Întrebări frecvente

Ce semnificație a interesului compus?

Dobânda compusă este dobânda calculată pe principal, precum și dobânda anterioară câștigată pe o perioadă fixă ​​de timp

Cum se calculează dobânda compusă?

Pentru a calcula dobânda compusă se calculează prima sumă finală, apoi se scade din principal pentru a obține dobânda compusă finală. Suma se calculează folosind formula,

A = P(1 + R/100) ^t

CI = A – P

Este dobânda compusă mai bună decât dobânda simplă pentru investitori?

Da, dobânda compusă este mult mai bună decât dobânda simplă pentru investitori.

Ce este Formula de dobândă compusă dacă este compusă zilnic?

Să presupunem că principalul dat este P, rata este R și intervalul de timp este T ani, atunci formula dobânzii compuse atunci când este compusă zilnic este:

A = P(1 + R/365) ^{{365 × T}}

Care este diferența dintre CI și SI?

Diferența de bază dintre CI și SI este că SI este dobânda percepută la suma principală, în timp ce CI este dobândă percepută pentru suma principală, precum și pentru dobânda acumulată la principal