Simbolurile seturilor sunt un termen colectiv folosit pentru toate simbolurile folosite în teoria mulțimilor, care este ramura matematicii care se ocupă cu colecția de obiecte și diferitele lor proprietăți. Un set este o colecție bine definită de obiecte în care fiecare obiect din colecție este numit element și fiecare element al setului urmează o regulă foarte specifică. În general, literele majuscule ale alfabetului englezesc sunt folosite pentru a desemna mulțimi, iar unele litere denotă unele seturi specifice în teoria mulțimilor.
Există multe simboluri folosite de-a lungul studiului acestei ramuri a matematicii, unele dintre simbolurile comune sunt {}, |, :, ∈, ∉, ⊆, U, Ø etc. Vom discuta în detaliu toate aceste simboluri în articol. inclusiv istoria acestor simboluri. Așadar, să începem călătoria noastră de a învăța despre diferite simboluri de mulțime diferite utilizate în teoria mulțimilor.
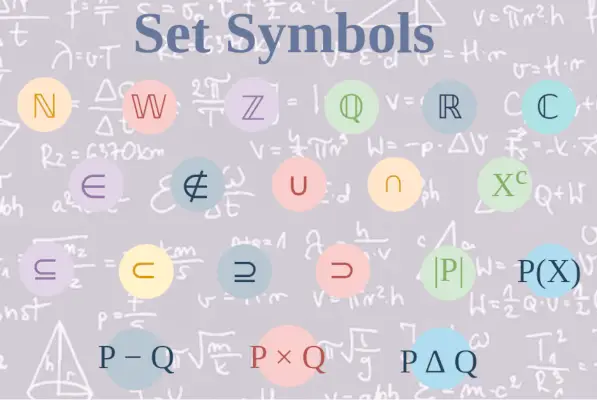
Cuprins
- Ce sunt simbolurile set?
- Istoria simbolurilor set
- Concepte de bază ale simbolurilor set
- Setați simboluri în matematică
- Simboluri ale teoriei seturilor
- Exemple rezolvate pe simboluri de set
- Întrebare de practică pentru simboluri set
- Întrebări frecvente
Ce sunt simbolurile set?
Simbolurile set sunt blocuri de bază ale matematicii care sunt folosite pentru a reprezenta și descrie grupuri de obiecte, numere sau elemente care au proprietăți similare. Aceste simboluri oferă o abordare clară și consecventă a comunicării ideilor dificile despre seturi și interacțiunile lor. Cel mai tipic simbol al setului este ∈, care reprezintă apartenența și se pronunță ca aparținând. ∈ indică faptul că un element face parte dintr-o anumită mulțime.
În schimb, ∉ înseamnă că un element nu face parte dintr-o mulțime. ⊆, ⊂, ∪, ∩, ∅ etc. sunt câteva dintre exemplele comune de simboluri în teoria mulțimilor. Aceste simboluri și alte simboluri le permit matematicienilor să definească operații, să specifice operațiuni și să formuleze afirmații matematice exacte, punând bazele pentru o varietate de specialități matematice și utilizări practice.
Citiți mai multe despre Teoria seturilor .
Exemplu de simboluri de set
Să folosim simbolul, care reprezintă intersecția mulțimilor, ca ilustrație. Fie E și F două mulțimi astfel încât Mulțimea E = {1, 3, 5, 7} și Mulțimea F = {3, 6, 9}. Atunci simbolul ∩ reprezintă intersecția dintre ambele mulțimi, adică E ∩ F.
Aici, E ∩ F conține toate elementele care sunt comune în ambele mulțimi E și F, adică {3}.
În concluzie, simbolul ∩ este folosit pentru a identifica elementele care sunt împărtășite de două sau mai multe mulțimi. Intersecția produce numai mulțimi care au elemente care sunt partajate de toate mulțimile care sunt intersectate.
Află mai multe despre Intersectia multimilor .
Istoria simbolurilor set
Între 1874 și 1897, un matematician german a sunat Georg Ferdinand Ludwig Philipp Cantor a dezvoltat o teorie abstractă numită Teoria seturilor. El a propus-o în timp ce cerceta unele preocupări faptice care implică forme specifice de seturi infinite de numere reale. O mulțime, conform noțiunii, este o grupare de anumite obiecte de observație definite și distincte. Toate aceste lucruri sunt denumite membri sau componente ale setului. Proprietatea combinațiilor de numere algebrice reale este fundamentul teoriei lui Cantor.
Concepte de bază ale simbolurilor set
Diferite idei sunt acoperite la diferite niveluri de școlarizare în teoria mulțimilor. Printre conceptele esențiale se numără reprezentarea seturilor, tipurile de mulțimi, operațiile seturilor (cum ar fi unirea și intersecția), cardinalitatea și relațiile seturilor și așa mai departe. Unele dintre conceptele esențiale din teoria mulțimilor sunt următoarele:
Set universal
Litera mare „U” este folosită în mod obișnuit pentru a reprezenta un set universal. De asemenea, este ocazional simbolizat prin ε(epsilon). Este un set care conține toate elementele altor seturi, precum și ale sale.
Complement de Set
Complementul unei mulțimi cuprinde toți constituenții mulțimii universale, cu excepția elementelor mulțimii examinate. Dacă A este o mulțime, atunci complementele sale vor conține toți membrii mulțimii universale specificate (U) care nu sunt incluse în A. Complementul unei mulțimi este indicat sau exprimat ca A’ sau Acși este definită ca:
A’= {x ∈ U: x ≠ A}
Citiți mai multe despre Complement de Set .
Setați notația Builder
Notația Set Builder este metoda de a reprezenta mulțimile în așa fel încât acolo unde nu trebuie să listăm toate elementele mulțimii, trebuie doar să specificăm regula care este urmată de toate elementele mulțimii. Câteva exemple ale acestor notații sunt:
Dacă A este o colecție de numere reale.
A = {x : x ∈ R}
Dacă A este o colecție de numere naturale.
A = {x : x> 0 și x ∈ Z]
Unde CU este un set de numere întregi.
Citeşte mai mult, Reprezentarea multimelor .
Setați simboluri în matematică
Pentru a face referire la diverse lucruri și sume, simbolul set utilizează frecvent o listă predefinită de simboluri variabile. Pentru a citi și a crea notații de set, trebuie mai întâi să înțelegeți cum să folosiți simboluri în diverse situații. Să ne uităm la toate notațiile și simbolurile teoriei mulțimilor referitoare la operații, relații și așa mai departe, împreună cu semnificațiile și exemplele lor, din această categorie.
Simboluri utilizate în sistemul numeric
Simbolurile utilizate în sistemele numerice sunt incluse în tabelul de mai jos:
| Simbol | Nume | Semnificație/Definiție | Exemplu |
|---|---|---|---|
| W sau 𝕎 | Numere întregi | Acestea sunt numerele naturale. | Știm N = {1, 2, 3, . . . } 1 ∈ N |
| N sau ℕ | Numere naturale | Numerele naturale sunt uneori denumite numere de numărare care încep cu 1. | Știm că W = {1, 2, 3, 4, 5, . . . } 0 ∈ W |
| Z sau ℤ | numere întregi | Numerele întregi sunt comparabile cu numerele întregi, cu excepția faptului că includ și valori negative. | Știm că Z = {. . . , -3, -2, -1, 0, 1, 2, 3 . . .} -6 ∈ Z |
| Q sau ℚ | Numere rationale | Numerele raționale sunt cele care sunt menționate ca a/b. În acest caz, a și b sunt numere întregi cu b ≠ 0. | Q= x=a/b, a, b ∈ Z și b ≠ 0 2/6 ∈ Q |
| P sau ℙ | Numere irationale | Acele numere care nu pot fi reprezentate sub forma a/b se numesc numere iraționale, adică toate numerele reale care nu sunt raționale. string compara cu java | P = x π și ∈ P |
| R sau ℝ | Numere reale | Numerele întregi, numerele raționale și numerele iraționale formează numerele reale. | R= x 6,343434 ∈ R |
| C sau ℂ | Numere complexe | Un număr complex este o combinație între un număr real și un număr imaginar. | C= z = a + bi, a, b ∈ R 6 + 2 i ∈ C |
Simboluri ale teoriei seturilor
Delimitatorii sunt caractere speciale sau secvențe de caractere care indică începutul sau sfârșitul unei anumite instrucțiuni sau corp de funcție a unui set specificat. Următoarele sunt simbolurile și semnificațiile teoriei seturilor de delimitatori:
| Simbol | Nume | Semnificație/Definiție | Exemplu |
|---|---|---|---|
| {} | A stabilit | În aceste paranteze se află o grămadă de elemente/ numere/ alfabete într-un set. | {15, 22, c, d} |
| | | Astfel încât | Acestea sunt folosite pentru a construi un set prin specificarea a ceea ce este conținut în el. | q> 6 Declarația specifică colecția tuturor q, astfel încât q este mai mare decât 6. |
| : | Astfel încât | Simbolul : este uneori folosit în loc de | simbol. | Propoziția de mai sus poate fi scrisă alternativ ca q . |
Mulțimi și simboluri relaționale în teoria mulțimilor
Simbolurile teoriei mulțimilor sunt folosite pentru a identifica o anumită mulțime, precum și pentru a determina/arăta o relație între mulțimi distincte sau relații în interiorul unei mulțimi, cum ar fi relația dintre o mulțime și constituentul acesteia. Tabelul de mai jos prezintă astfel de simboluri de relație, împreună cu semnificațiile și exemplele lor:
| Simbol | Nume | Semnificație/Definiție | Exemplu |
|---|---|---|---|
| a ∈ A | Este o componentă a | Aceasta specifică faptul că un element este membru al unui anumit set. | Dacă o mulțime A={12, 17, 18, 27} putem spune că 27 ∈ a. |
| b ∉ B | Nu este o componentă a | Aceasta indică faptul că un element nu aparține unui anumit set. | Dacă o mulțime B={c, d, g, h, 32, 54, 59} atunci orice element altul decât cel din mulțime nu aparține acestei mulțimi. De exemplu, 18 ∉ B. |
| A = B | Relația de egalitate | Seturile furnizate sunt echivalente în sensul că au aceleași componente. | Dacă puneți P={16, 22, a} și Q={16, 22, a} atunci P=Q. |
| A ⊆ B | Subset | Când toate elementele lui A sunt prezente în B, A este o submulțime a lui B. | A= {31, b} și B={a, b, 31, 54} {31, b} ⊆ {a, b, 31, 54} |
| A ⊂ B | Subset adecvat | Se spune că P este o submulțime propriu-zisă a lui B când este o submulțime a lui B și nu este egală cu B. | A= {24, c} și B={a, c, 24, 50} A ⊂ B |
| A ⊄ B | Nu un subset | Ca urmare, mulțimea A nu este o submulțime a mulțimii B. | A = {67,52} și B = {42,34,12} A ⊄ B if else if else if java |
| A ⊇ B | Superset | A este un superset al lui B dacă setul B este un subset al lui A. Setul A poate fi același sau mai mare decât setul B. | A = {14, 18, 26} și B = {14, 18, 26} {14, 18, 26} ⊇{14, 18, 26} |
| A ⊃ B | Superset adecvat | Mulțimea A are mai multe elemente decât mulțimea B, deoarece este o supramulțime a lui B. | {14, 18, 26, 42} ⊃ {18,26} |
| A ⊅ B | Nu un Superset | Când toate elementele lui B nu sunt prezente în A, A nu este o supramulțime adevărată a lui B. | A = {11, 12, 16} și B = {11, 19} {11, 12, 16} ⊅ {11, 19} |
| Ø | Set gol | Un set gol sau nul este unul care nu include niciun element. | {22, y} ∩ {33, a} = Ø |
| ÎN | Set universal | Un set care conține elemente din toate seturile relevante, inclusiv ale sale. | Dacă A = {a,b,c} și B = {1,2,3,b,c}, atunci U = {1,2,3,a,b,c} |
| |A| sau n{A} | Cardinalitatea unui set | Cardinalitatea se referă la numărul de articole dintr-o anumită colecție. | Dacă A= {17, 31, 45, 59, 62}, atunci |A|=5. |
| P(X) | Set de putere | Un set de puteri este multimea tuturor submultimii multimii X, inclusiv multimea in sine si multimea nula. | Dacă, X = {12, 16, 19} P(X) = {12, 16, 19}={{}, {12}, {16}, {19}, {12, 16}, {16, 19}, {12, 19}, {12, 16, 19}} |
Simboluri bazate pe operatori în teoria mulțimilor
Cu exemple, vom studia simbolurile și semnificațiile teoriei seturilor pentru numeroase operații, cum ar fi unirea, complementul, intersecția, diferența și altele.
| Simbol | Nume | Semnificație/Definiție | Exemplu |
|---|---|---|---|
| A ∪ B | Unirea de seturi | Uniunea de seturi creează un set complet nou prin combinarea tuturor componentelor din seturile furnizate. | A = {p, q, u, v, w} B = {r, s, x, y} A ∪ B (A uniune B) = {p, q, u, v, w, r, s, x, y} |
| A ∩ B | Intersectia multimilor | Componenta comună a ambelor mulțimi este inclusă în intersecție. | A = { 4, 8, a, b} și B = {3, 8, c, b}, apoi A ∩ B = {8, b} |
| XcSAUX' | Complement al unui set | Complementul unui set cuprinde toate lucrurile care nu aparțin setului furnizat. | Dacă A este mulțime universală și A = {3, 6, 8, 13, 15, 17, 18, 19, 22, 24} și B = {13, 15, 17, 18, 19} atunci X′ = A – B ⇒ X′ = {3, 6, 8, 22, 24} |
| A - B | Setați diferența | Setul de diferențe este un set care conține articole dintr-un set care nu se găsesc în altul. | A = {12, 13, 15, 19} și B = {13, 14, 15, 16, 17} A – B = {12, 19} |
| A × B | Produsul cartezian al multimelor | Un produs cartezian este produsul componentelor ordonate ale mulțimilor. | A = {4, 5, 6} și B = {r} Acum, A × B ={(4, r), (2, r), (6, r)} |
| A ∆ B | Diferența simetrică a mulțimilor | A Δ B = (A – B) U (B – A) denotă diferența simetrică. | A = {13, 19, 25, 28, 37}, B = {13, 25, 55, 31} A ∆ B = { 19, 28, 37, 55, 31} |
Citeşte mai mult
- Tipuri de seturi
- Operare pe platouri
Exemple rezolvate pe simboluri de set
Exemplul 1: Având în vedere două mulțimi cu P={21, 32, 43, 54, 65, 75} și Q={21, 43, 65, 75, 87, 98} care este valoarea lui P∪Q?
Răspuns:
P={21, 32, 43, 54, 65, 75} și Q={21, 43, 65, 75, 87, 98}
P∪Q={21, 32, 43, 54, 65, 75, 87, 98}
Exemplul 2: Care este valoarea lui |Y| dacă Y={13, 19, 25, 31, 42, 65}?
Răspuns:
|Y| = Cardinalitatea multimii=numarul de elemente din multime este solutia.
|Y| = n(Y)=6, deoarece mulțimea Y are 6 elemente.
Exemplul 3: Având în vedere două mulțimi cu valorile P={a,c,e} și Q={4,3}, determinați produsul lor cartezian.
Răspuns:
Produsul cartezian = P × Q
Dacă P={b, d, f} și Q={5, 6}
Atunci P × Q={(b,5), (d,6), (b,5), (d,6), (b,5), (d,6), (b,5), (d ,6), (b,5), (d,6)}
Exemplul 4: Să presupunem că P = {x: x este un număr întreg natural și un multiplu de 24, iar Q = {x: x este un număr natural mai mic decât 8}. Determinați P ∪ Q.
Răspuns:
Dat fiind
P = {1, 2, 3, 4, 6, 8, 12, 24}
actor shweta tiwariQ = {1, 2, 3, 4, 5, 6, 7}
Ca rezultat, P ∪ Q = {1, 2, 3, 4, 5, 6, 7, 8, 12, 24}
Exemplul 5: Să presupunem că P = {3, 5, 7}, Q = {2, 3, 4, 6}. Găsiți (P ∩ Q)’.
Răspuns:
Dat, P = {4, 6, 8}, Q = {3, 4, 5, 7}
P ∩ Q = {4}
Prin urmare,
(P ∩ Q)’ = {3, 5, 6, 7, 8}
Exemplul 6: Dacă P = {4, 5, 7, 8, 9, 10} și Q = {3, 5, 7, 9, 12, 14}, determinați
(i) P-Q și (ii) P-Q.
Răspuns:
Dat,
P = {4, 5, 7, 8, 9, 10} și Q = {3, 5, 7, 9, 12, 14}
(i) P – Q = {4, 8, 10}
(ii) Q – P = {3, 12, 14}
Întrebări practice pentru simboluri de set
Intrebarea 1: Având în vedere seturile:
- A = {2, 4, 6, 8}
- B = {4, 8, 12, 16}
Determinați elementele din uniunea mulțimilor A și B.
Intrebarea 2: Să luăm în considerare seturile:
- X = {1, 2, 3, 4, 5}
- Y = {3, 4, 5, 6, 7}
Aflați intersecția mulțimilor X și Y.
Întrebarea 3: Să presupunem că aveți seturile:
- P = {a, b, c, d}
- Q = {c, d, e, f}
Calculați elementele din mulțimea P – Q precum și Q – P.
Întrebarea 4: Să presupunem că aveți seturile:
- U = {1, 2, 3, 4, 5}
- V = {4, 5, 6, 7}
Aflați dacă mulțimea V este o submulțime a mulțimii U.
Întrebarea 5: Luați în considerare seturile:
- S = {mere, banane, portocale, pere}
- T = {pere, mango, cireș}
Aflați produsul cartezian al mulțimilor S și T.
Întrebarea 6: Să presupunem că aveți setul universal:
- U = {a, b, c, d, e, f, g, h, i, j}
Si seturile:
- E = {b, d, f, h, j}
- F = {a, c, e, g, i}
Calculați complementul mulțimii E și F față de mulțimea universală U.
Întrebări frecvente despre setarea simbolurilor
1. Definiți simbolul set.
Simbolul mulțimii este o ramură care studiază grupările de entități/numere/obiecte, relațiile acestora cu alte mulțimi, diferite operații (unire, intersecție, complement și diferență) și caracteristicile asociate.
2. Ce reprezintă acest simbol ⊆?
Simbolul ⊆ înseamnă că este o submulțime a. Un subset este o mulțime ale cărei elemente au fost adăugate ca și cum ar fi toate elementele unui alt set.
3. Ce înseamnă ∪ în mulțimi?
„∪” este semnul pentru unirea set. A ∪ B este o mulțime care conține toate elementele mulțimilor A și B.
4. Ce reprezintă P = Q?
Dacă mulțimea P este egală cu mulțimea Q, atunci membrii lui P și Q sunt aceiași. De exemplu:
P = {4,5,6} și Q = {6,5,4}
Ca rezultat, P = Q.
5. În matematică, ce înseamnă ∩?
„∩” înseamnă unirea a două mulțimi. A ∩ B este o mulțime care conține elemente împărtășite atât de A, cât și de B.
6. Ce este ∈ în mulțimi?
∈ este un semn care înseamnă „aparține”. Dacă b ∈ B, indică faptul că b este un element al lui B.
7. Care este mulțimea N ={1, 2, 3, 4, 5, . . .} cunoscut ca?
Mulțimea numerelor naturale este definită ca N = {1, 2, 3, 4, 5, …} Conține toate numerele pozitive, de la 1 la un număr infinit. Această colecție este crucială pentru matematică și oferă un cadru atât pentru ordonare, cât și pentru numărare.
8. Ce este A × B în mulțimi?
Produsul cartezian al mulțimilor A și B este prezentat ca A x B în simbolul mulțimii. Este mulțimea care include toate perechile ordonate posibile în care primul element este extras din mulțimea A și al doilea din mulțimea B.
9. Cum vei citi A ∩ B?
A∩B se pronunță A intersecție B. Acesta reprezintă mulțimea care conține elemente care sunt comune în ambele mulțimi.
10. Ce înseamnă Ø în teoria mulţimilor?
În teoria mulțimilor, ideea de mulțime goală, care nu are elemente, este notă prin simbolul Ø (pronunțat mulțime goală).
11. Ce este AUB?
AUB în matematică înseamnă unirea mulțimilor A și B. Se referă la mulțimea care include fiecare element din ambele mulțimi A și B.
12. Este ∅ la fel cu {}?
Da, ∅ și {} reprezintă ambele mulțimi goale în matematică. Astfel, ambele sunt notații diferite ale aceluiași lucru.
