În lumea reală învățare automată aplicații, este obișnuit să aibă multe caracteristici relevante, dar numai un subset dintre ele poate fi observabil. Când avem de-a face cu variabile care sunt uneori observabile și alteori nu, este într-adevăr posibil să se utilizeze cazurile în care acea variabilă este vizibilă sau observată pentru a învăța și a face predicții pentru cazurile în care nu este observabilă. Această abordare este adesea denumită gestionarea datelor lipsă. Folosind cazurile disponibile în care variabila este observabilă, algoritmii de învățare automată pot învăța modele și relații din datele observate. Aceste modele învățate pot fi apoi utilizate pentru a prezice valorile variabilei în cazurile în care aceasta lipsește sau nu este observabilă.
Algoritmul de așteptare-Maximizare poate fi utilizat pentru a gestiona situații în care variabilele sunt parțial observabile. Când anumite variabile sunt observabile, putem folosi acele instanțe pentru a învăța și a estima valorile lor. Apoi, putem prezice valorile acestor variabile în cazurile în care nu este observabilă.
Algoritmul EM a fost propus și numit într-o lucrare fundamentală publicată în 1977 de Arthur Dempster, Nan Laird și Donald Rubin. Lucrările lor au oficializat algoritmul și au demonstrat utilitatea acestuia în modelarea și estimarea statistică.
Algoritmul EM este aplicabil variabilelor latente, care sunt variabile care nu sunt direct observabile, dar sunt deduse din valorile altor variabile observate. Utilizând forma generală cunoscută a distribuției de probabilitate care guvernează aceste variabile latente, algoritmul EM poate prezice valorile acestora.
Algoritmul EM servește drept bază pentru mulți algoritmi de clustering nesupravegheați în domeniul învățării automate. Acesta oferă un cadru pentru a găsi parametrii de probabilitate maximă locali ai unui model statistic și pentru a deduce variabile latente în cazurile în care datele lipsesc sau sunt incomplete.
Algoritmul de așteptare-maximizare (EM).
Algoritmul Expectation-Maximization (EM) este o metodă de optimizare iterativă care combină diferite nesupravegheate învățare automată algoritmi pentru a găsi probabilitatea maximă sau estimările posterioare maxime ale parametrilor în modelele statistice care implică variabile latente neobservate. Algoritmul EM este utilizat în mod obișnuit pentru modelele variabile latente și poate gestiona datele lipsă. Constă dintr-o etapă de estimare (pasul E) și un pas de maximizare (pasul M), formând un proces iterativ pentru a îmbunătăți potrivirea modelului.
- În pasul E, algoritmul calculează variabilele latente, adică așteptarea log-probabilității utilizând estimările actuale ale parametrilor.
- În pasul M, algoritmul determină parametrii care maximizează log-probabilitatea așteptată obținută în pasul E, iar parametrii modelului corespunzători sunt actualizați pe baza variabilelor latente estimate.

Aşteptări-Maximizare în algoritmul EM
Prin repetarea iterativă a acestor pași, algoritmul EM încearcă să maximizeze probabilitatea datelor observate. Este folosit în mod obișnuit pentru sarcini de învățare nesupravegheate, cum ar fi gruparea, unde variabilele latente sunt deduse și are aplicații în diverse domenii, inclusiv învățarea automată, viziunea computerizată și procesarea limbajului natural.
Termeni cheie în algoritmul de așteptare-maximizare (EM).
Unii dintre termenii cheie cei mai des folosiți în algoritmul de maximizare a așteptărilor (EM) sunt următorii:
funcțiile arduino
- Variabile latente: variabilele latente sunt variabile neobservate în modelele statistice care pot fi deduse doar indirect prin efectele lor asupra variabilelor observabile. Ele nu pot fi măsurate direct, dar pot fi detectate prin impactul lor asupra variabilelor observabile. Probabilitate: Este probabilitatea de a observa datele date având în vedere parametrii modelului. În algoritmul EM, scopul este de a găsi parametrii care maximizează probabilitatea. Log-Likelihood: este logaritmul funcției de probabilitate, care măsoară bunătatea potrivirii dintre datele observate și model. Algoritmul EM caută să maximizeze log-probabilitatea. Estimarea maximă a probabilității (MLE) : MLE este o metodă de estimare a parametrilor unui model statistic prin găsirea valorilor parametrilor care maximizează funcția de probabilitate, care măsoară cât de bine modelul explică datele observate. Probabilitatea posterioară: În contextul inferenței bayesiene, algoritmul EM poate fi extins pentru a estima estimările maxime a posteriori (MAP), unde probabilitatea posterioară a parametrilor este calculată pe baza distribuției anterioare și a funcției de probabilitate. Pasul de așteptare (E): Pasul E al algoritmului EM calculează valoarea așteptată sau probabilitatea posterioară a variabilelor latente având în vedere datele observate și estimările parametrilor curenti. Aceasta implică calcularea probabilităților fiecărei variabile latente pentru fiecare punct de date. Pasul de maximizare (M): Pasul M al algoritmului EM actualizează estimările parametrilor prin maximizarea probabilității log-probabilitate așteptată obținută din pasul E. Aceasta implică găsirea valorilor parametrilor care optimizează funcția de probabilitate, de obicei prin metode de optimizare numerică. Convergență: Convergența se referă la condiția în care algoritmul EM a ajuns la o soluție stabilă. De obicei, se determină prin verificarea dacă modificarea probabilității logaritmice sau a estimărilor parametrilor scade sub un prag predefinit.
Cum funcționează algoritmul de maximizare a așteptărilor (EM):
Esența algoritmului de așteptare-maximizare este de a utiliza datele observate disponibile ale setului de date pentru a estima datele lipsă și apoi de a utiliza acele date pentru a actualiza valorile parametrilor. Să înțelegem în detaliu algoritmul EM.

Diagrama de flux al algoritmului EM
- Inițializare:
- Inițial, se ia în considerare un set de valori inițiale ale parametrilor. Un set de date observate incomplete este dat sistemului cu presupunerea că datele observate provin de la un model specific.
- Calculați probabilitatea sau responsabilitatea posterioară a fiecărei variabile latente, având în vedere datele observate și estimările actuale ale parametrilor.
- Estimați valorile datelor lipsă sau incomplete utilizând estimările actuale ale parametrilor.
- Calculați log-probabilitatea datelor observate pe baza estimărilor actuale ale parametrilor și a datelor estimate lipsă.
- Actualizați parametrii modelului prin maximizarea probabilității de înregistrare a datelor complete așteptate, obținute din pasul E.
- Aceasta implică de obicei rezolvarea problemelor de optimizare pentru a găsi valorile parametrilor care maximizează log-probabilitatea.
- Tehnica specifică de optimizare utilizată depinde de natura problemei și de modelul utilizat.
- Verificați convergența comparând modificarea log-probabilității sau a valorilor parametrilor între iterații.
- Dacă modificarea este sub un prag predefinit, opriți-vă și considerați algoritmul convergent.
- În caz contrar, reveniți la pasul E și repetați procesul până când se obține convergența.
Implementarea pas cu pas al algoritmului de maximizare a așteptărilor
Importați bibliotecile necesare
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
defini computerul
>
>
Generați un set de date cu două componente gaussiene
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
cuvânt cheie static în java
Ieșire :

Graficul de densitate
Inițializați parametrii
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Efectuați algoritmul EM
- Iterează pentru numărul specificat de epoci (20 în acest caz).
- În fiecare epocă, pasul E calculează responsabilitățile (valorile gamma) prin evaluarea densităților de probabilitate gaussiene pentru fiecare componentă și ponderându-le cu proporțiile corespunzătoare.
- Pasul M actualizează parametrii calculând media ponderată și abaterea standard pentru fiecare componentă
Python3
vlc descărca videoclipuri de pe youtube
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Ieșire :

Epocă vs Log-probabilitate
Reprezentați grafic densitatea estimată finală
Python3
lista imuabilă java
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Ieșire :
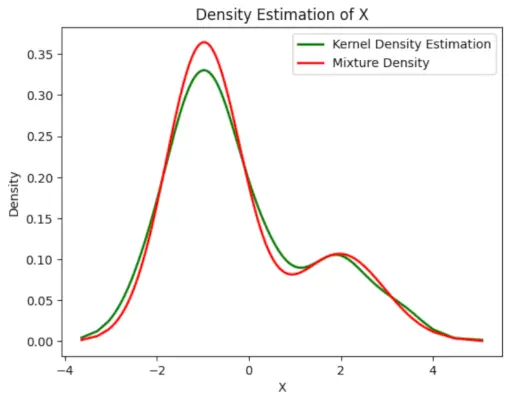
Densitatea estimată
Aplicații ale algoritmul EM
- Poate fi folosit pentru a completa datele lipsă dintr-un eșantion.
- Poate fi folosit ca bază pentru învățarea nesupravegheată a clusterelor.
- Poate fi utilizat în scopul estimării parametrilor modelului Markov ascuns (HMM).
- Poate fi folosit pentru descoperirea valorilor variabilelor latente.
Avantajele algoritmului EM
- Este întotdeauna garantat că probabilitatea va crește cu fiecare iterație.
- Pasul E și pasul M sunt adesea destul de ușori pentru multe probleme în ceea ce privește implementarea.
- Soluțiile la pașii M există adesea în formă închisă.
Dezavantajele algoritmului EM
- Are convergență lentă.
- Face convergență numai către optima locală.
- Necesită atât probabilitățile, înainte și înapoi (optimizarea numerică necesită doar probabilitate înainte).
