Triunghiurile sunt poligoane închise cu trei laturi formate prin intersecția a trei drepte. Se intalneste foarte mult in viata de zi cu zi. Este una dintre formele de bază ale geometriei. Are trei laturi, trei unghiuri și trei vârfuri. Un triunghi dreptunghic este unul în care unul dintre unghiuri este întotdeauna egal cu 90°. Teorema lui Pitagora este derivat pentru triunghiuri dreptunghiulare, care afirmă că pătratul ipotenuzei (cea mai lungă latură) este egal cu suma pătratelor bazei și perpendicularei.

Având în vedere lungimea a cel puțin două laturi ale unui triunghi dreptunghic, putem găsi valoarea oricărui unghi al triunghiului dreptunghic. Pentru aceasta, folosim diverse funcții trigonometrice precum sinus, cosinus, tangentă, cotangentă, sec și cosec. Acestea ne ajută să relaționăm unghiurile unui triunghi dreptunghic cu laturile sale.

Proprietăți

• Există un vârf în unghi drept printre cele trei vârfuri
• Latura opusă vârfului în unghi drept se numește ipotenuză .
• Lungimea laturilor urmează teorema lui Pitagora, care afirmă

ipotenuză ² = baza ² + altitudine ²

• Ipotenuza este cea mai lungă latură a unui triunghi dreptunghic.
• Altele unghiuri decât unghiul drept sunt unghiuri ascuțite, deoarece valoarea este mai mică de 90^O

Funcții trigonometrice

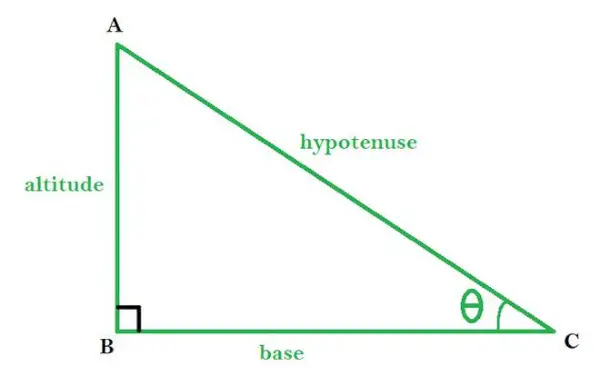
ABC este un triunghi dreptunghic cu ∠B drept unghi drept

matrice de șiruri în programarea c

• cosθ: Aceasta dă raportul bazei cu ipotenuza unui triunghi dreptunghic.

cosθ = baza / ipotenuza

• sinθ: Aceasta dă raportul dintre altitudine și ipotenuza unui triunghi dreptunghic.

sinθ = altitudine / ipotenuză

• tanθ: Este raportul dintre altitudinea de baza unui triunghi dreptunghic.

tanθ = altitudine/bază

• cotθ: Este inversul lui tanθ
• secθ: Este inversul cosθ
• cosecθ: Este inversul sinθ

Pentru a găsi unghiurile unui triunghi dreptunghic, putem lua inversul trigonometric al raportului laturilor date ale triunghiului.

Exemplu:

Dacă sinθ = x, atunci putem scrie

θ = sin ^-1 X.

Aceasta returnează unghiul pentru care valoarea sinusului unghiului este x.

În mod similar, există cos^-1θ, deci^-1eu, patut^-1θ, sec^-1θ și cosec^-1i

Exemple de probleme

Întrebarea 1. Având în vedere un triunghi dreptunghic, cu baza este egală cu 10 cm și ipotenuza este egală cu 20 cm. Aflați valoarea unghiului de bază.

Soluţie:

Dat, baza = 10cm

Hipotenuza = 20cm

Fie valoarea unghiului de bază θ. Putem scrie

cosθ = baza / ipotenuza = 10/20 = 1/2

θ = cos^-1(1/2) = 60^O

Astfel, valoarea unghiului de bază este 60 ^O .

Întrebarea 2. Aflați valoarea unghiurilor unui triunghi dreptunghic, având în vedere că unul dintre unghiurile ascuțite este dublul celuilalt.

Soluţie:

Deoarece știm că suma tuturor celor trei unghiuri dintr-un triunghi este 180^O.

Deoarece unul dintre unghiuri este de 90^Oiar unul dintre unghiurile ascuțite este de două ori față de celălalt, le putem considera ca θ și 2θ.

Deci, putem scrie

90^O+ θ + 2θ = 180^O

3θ = 180^O– 90^O

3θ = 90^O

θ = 90^O/3 = 30 ^O

2θ = 2 × 30^O= 60 ^O

Deci, unghiurile sunt 30 ^O , 60 ^O , și 90 ^O .

Întrebarea 3. Aflați valoarea unghiului de înălțime al unei scări cu lungimea de 5m, având în vedere că baza scării se află la o distanță de 3m de perete.

Soluţie:

Deoarece scara acționează ca o ipotenuză a unui triunghi dreptunghic și distanța la bază este egală cu 3 m, putem scrie

Hipotenuza = 5m

Baza = 3m

Fie unghiul de elevație θ. Deci, putem scrie

cosθ = Baza / Hipotenuza = 3/5

θ = cos^-1(3/5)

θ = 53^O

Astfel, valoarea unghiului de elevație este 53^O.

Întrebarea 4. Aflați valoarea ipotenuzei, având în vedere că lungimea altitudinii este de 8m și unghiul de bază este egal cu 30 ^O .

Soluţie:

Având în vedere, unghiul de bază este egal cu 30^Oiar altitudinea este egală cu 8m, putem aplica funcția sinus pentru a găsi lungimea ipotenuzei.

păcat30 ^O = altitudine / ipotenuză

ipotenuza = altitudine / sin30^O

Din moment ce valoarea sin30^Oeste egal cu 1/2, putem scrie

ipotenuza = altitudine / (1/2) = 2 × altitudine

Astfel, ipotenuza = 2 × 8 = 16m

Astfel, lungimea ipotenuzei este egală cu 16m.