Acest tutorial este un ghid pentru începători învățarea structurilor de date și a algoritmilor folosind Python. În acest articol, vom discuta despre structurile de date încorporate, cum ar fi liste, tupluri, dicționare etc. și unele structuri de date definite de utilizator, cum ar fi liste legate , copaci , grafice , etc, și parcurgerea, precum și algoritmii de căutare și sortare cu ajutorul exemplelor și întrebărilor practice bune și bine explicate.

Liste

Liste Python sunt colecții ordonate de date la fel ca matricele în alte limbaje de programare. Permite diferite tipuri de elemente din listă. Implementarea Python List este similară cu Vectors în C++ sau ArrayList în JAVA. Operațiunea costisitoare este inserarea sau ștergerea elementului de la începutul Listei, deoarece toate elementele trebuie să fie mutate. Inserarea și ștergerea la sfârșitul listei pot deveni costisitoare și în cazul în care memoria prealocată devine plină.

Exemplu: Crearea listei Python

List = [1, 2, 3, 'GFG', 2.3] print(List)>

[1, 2, 3, 'GFG', 2.3]>

Elementele listei pot fi accesate prin indexul atribuit. În indexul de pornire python al listei, o secvență este 0, iar indexul final este (dacă există N elemente) N-1.

Exemplu: Operații Python Listă

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3])>

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks>

Tuplu

Tupluri Python sunt similare listelor, dar tuplurile sunt imuabil în natură, adică odată creat nu poate fi modificat. La fel ca o Listă, un tuplu poate conține și elemente de diferite tipuri.

În Python, tuplurile sunt create prin plasarea unei secvențe de valori separate prin „virgulă” cu sau fără utilizarea parantezelor pentru gruparea secvenței de date.

Notă: Pentru a crea un tuplu dintr-un element trebuie să existe o virgulă finală. De exemplu, (8,) va crea un tuplu care conține 8 ca element.

Exemplu: Operații cu tuplu Python

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3])>

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4>

A stabilit

Set Python este o colecție mutabilă de date care nu permite nicio duplicare. Seturile sunt folosite practic pentru a include testarea membrilor și eliminarea intrărilor duplicate. Structura de date folosită în aceasta este Hashing, o tehnică populară pentru a efectua inserarea, ștergerea și traversarea în O(1) în medie.

Dacă mai multe valori sunt prezente la aceeași poziție de index, atunci valoarea este atașată la acea poziție de index, pentru a forma o listă legată. În, seturile CPython sunt implementate folosind un dicționar cu variabile fictive, în care ființele cheie pe care membrii le setează cu optimizări mai mari la complexitatea timpului.

Set de implementare:

Seturi cu numeroase operații pe un singur HashTable:

Exemplu: Operații de set Python

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set)>

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True>

Seturi congelate

Seturi congelate în Python sunt obiecte imuabile care acceptă doar metode și operatori care produc un rezultat fără a afecta setul sau seturile înghețate la care sunt aplicate. În timp ce elementele unui set pot fi modificate în orice moment, elementele setului înghețat rămân aceleași după creare.

Exemplu: set Python Frozen

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h')>

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'})>

Şir

șiruri Python este matricea imuabilă de octeți reprezentând caractere Unicode. Python nu are un tip de date caracter, un singur caracter este pur și simplu un șir cu lungimea de 1.

Notă: Deoarece șirurile sunt imuabile, modificarea unui șir va duce la crearea unei noi copii.

Exemplu: Operații cu șiruri Python

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1])>

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s>

Dicţionar

Dicționar Python este o colecție neordonată de date care stochează date în formatul pereche cheie:valoare. Este ca tabelele hash în orice altă limbă cu complexitatea de timp a O(1). Indexarea dicționarului Python se face cu ajutorul tastelor. Acestea sunt de orice tip hashable, adică un obiect al cărui obiect nu se poate schimba niciodată, cum ar fi șiruri, numere, tupluri etc. Putem crea un dicționar folosind acolade ({}) sau înțelegere a dicționarului.

Exemplu: Python Dictionary Operations

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict)>

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25}>

Matrice

O matrice este o matrice 2D în care fiecare element are strict aceeași dimensiune. Pentru a crea o matrice, vom folosi Pachetul NumPy .

Exemplu: Python NumPy Matrix Operations

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m)>

Ieșire

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]]>

Bytearray

Python Bytearray oferă o secvență mutabilă de numere întregi în intervalul 0 <= x < 256.

Exemplu: Operații Python Bytearray

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a)>

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')>

Lista legată

A lista legată este o structură de date liniară, în care elementele nu sunt stocate în locații de memorie contigue. Elementele dintr-o listă legată sunt legate folosind pointeri, așa cum se arată în imaginea de mai jos:

conversia șirului de caractere în întreg în java

O listă legată este reprezentată de un pointer către primul nod al listei legate. Primul nod se numește cap. Dacă lista legată este goală, atunci valoarea capului este NULL. Fiecare nod dintr-o listă constă din cel puțin două părți:

• Date
• Indicator (sau referință) către următorul nod

Exemplu: definirea listei legate în Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None>

Să creăm o listă simplă legată cu 3 noduri.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | nul | | 3 | nul |  +----+------+ +----+------+ +----+------+ ''' secunda.next = a treia ; # Conectați cel de-al doilea nod cu al treilea nod ''' Acum următorul nod al doilea se referă la al treilea. Deci toate cele trei noduri sunt legate.  llist.cap al doilea treime | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | nul |  +----+------+ +----+------+ +----+------+ '''>

Traversarea listelor conectate

În programul anterior, am creat o listă simplă legată cu trei noduri. Să parcurgem lista creată și să imprimăm datele fiecărui nod. Pentru traversare, să scriem o funcție de uz general printList() care tipărește orice listă dată.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()>

1 2 3>

Mai multe articole pe Linked List

• Inserarea listelor legate
• Ștergerea listelor legate (Ștergerea unei chei date)
• Ștergerea listelor legate (Ștergerea unei chei la o anumită poziție)
• Găsiți lungimea unei liste legate (iterativ și recursiv)
• Căutați un element într-o listă legată (iterativ și recursiv)
• Al-lea nod de la sfârșitul unei liste legate
• Inversați o listă legată

A grămadă este o structură de date liniară care stochează articole într-o manieră Last-In/First-Out (LIFO) sau First-In/Last-Out (FILO). În stivă, un element nou este adăugat la un capăt și un element este eliminat numai de la acel capăt. Operațiile de inserare și ștergere sunt adesea numite push și pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty>

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []>

Ca o stivă, coadă este o structură de date liniară care stochează articole într-o manieră First In First Out (FIFO). Cu o coadă, articolul adăugat cel mai puțin recent este eliminat mai întâi. Un bun exemplu de coadă este orice coadă de consumatori pentru o resursă în care consumatorul care a venit primul este servit primul.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty>

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []>

Cozi prioritare sunt structuri de date abstracte în care fiecare dată/valoare din coadă are o anumită prioritate. De exemplu, în companiile aeriene, bagajele cu titlul Business sau First-class ajung mai devreme decât restul. Priority Queue este o extensie a cozii cu următoarele proprietăți.

• Un element cu prioritate mare este scos din coadă înaintea unui element cu prioritate scăzută.
• Dacă două elemente au aceeași prioritate, acestea sunt servite în funcție de ordinea lor în coadă.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max]: max = i item = self.queue[max] del self.queue[max] returnează elementul cu excepția IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) în timp ce nu myQueue.isEmpty(): print(myQueue.delete())>

12 1 14 7 14 12 7 1>

Morman

modulul heapq în Python furnizează structura de date heap care este utilizată în principal pentru a reprezenta o coadă prioritară. Proprietatea acestei structuri de date este că oferă întotdeauna cel mai mic element (heap min) ori de câte ori elementul apare. Ori de câte ori elementele sunt împinse sau sparte, structura heap este menținută. Elementul heap[0] returnează, de asemenea, cel mai mic element de fiecare dată. Acceptă extragerea și inserarea celui mai mic element în timpii O(log n).

În general, Heap-urile pot fi de două tipuri:

• Max-Heap: Într-un Max-Heap, cheia prezentă la nodul rădăcină trebuie să fie cea mai mare dintre cheile prezente la toți copiii săi. Aceeași proprietate trebuie să fie adevărată recursiv pentru toți sub-arborele din acel Arbore Binar.
• Min-Heap: Într-un Min-Heap, cheia prezentă la nodul rădăcină trebuie să fie minimă dintre cheile prezente la toți copiii săi. Aceeași proprietate trebuie să fie adevărată recursiv pentru toți sub-arborele din acel Arbore Binar.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li))>

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1>

Mai multe articole despre Heap

• Heap binar
• Cel mai mare element al K-a dintr-o matrice
• Cel mai mic/cel mai mare element K’ din matricea nesortată
• Sortați o matrice aproape sortată
• K-a cea mai mare sumă Subbarray contiguă
• Suma minimă a două numere formată din cifrele unui tablou

Un arbore este o structură de date ierarhică care arată ca figura de mai jos -

 tree  ----  j <-- root  /   f k  /   a h z <-- leaves>

Nodul cel mai de sus al arborelui se numește rădăcină, în timp ce nodurile cele mai de jos sau nodurile fără copii sunt numite nodurile frunzelor. Nodurile care sunt direct sub un nod sunt numite copii ale acestuia, iar nodurile care sunt direct deasupra unui nod sunt numite părinte.

A arbore binar este un copac ale cărui elemente pot avea aproape doi copii. Deoarece fiecare element dintr-un arbore binar poate avea doar 2 copii, de obicei îi numim copii stânga și dreapta. Un nod de arbore binar conține următoarele părți.

• Date
• Indicator către copilul stâng
• Indicator către copilul potrivit

Exemplu: Definirea clasei de nod

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key>

Acum să creăm un arbore cu 4 noduri în Python. Să presupunem că structura arborelui arată ca mai jos -

 tree  ----  1 <-- root  /   2 3   /  4>

Exemplu: Adăugarea de date în arbore

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None'''>

Traversarea copacului

Copacii pot fi traversați în diverse feluri. Următoarele sunt modalitățile utilizate în general pentru traversarea copacilor. Să luăm în considerare arborele de mai jos -

 tree  ----  1 <-- root  /   2 3   /  4 5>

Primele traversări de adâncime:

conversia șir la dată

• În ordine (stânga, rădăcină, dreapta): 4 2 5 1 3
• Precomandă (rădăcină, stânga, dreapta): 1 2 4 5 3
• Post-comanda (stânga, dreapta, rădăcină): 4 5 2 3 1

Algoritm Inorder(arboresc)

• Traversați subarborele din stânga, adică apelați Inorder(subarborele stânga)
• Vizitați rădăcina.
• Traversați subarborele din dreapta, adică apelați Inorder (subarborele din dreapta)

Precomandă algoritm (arboresc)

• Vizitați rădăcina.
• Traversați subarborele din stânga, adică apelați Precomanda (subarborele stânga)
• Traversați subarborele din dreapta, adică apelați Precomanda (subarborele din dreapta)

Algoritm Ordin poștal(arboresc)

• Traversați subarborele din stânga, adică apelați Postorder(subarborele stânga)
• Traversați subarborele din dreapta, adică apelați Postorder (subarborele din dreapta)
• Vizitați rădăcina.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root)>

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1>

Complexitatea timpului – O(n)

Lățimea-Primul nivel sau traversarea comenzii

Parcursul nivelului de ordine a unui copac este parcurgerea pe lățimea întâi pentru copac. Parcurgerea în ordinea nivelurilor a arborelui de mai sus este 1 2 3 4 5.

Pentru fiecare nod, mai întâi, nodul este vizitat și apoi nodurile sale secundare sunt puse într-o coadă FIFO. Mai jos este algoritmul pentru același -

• Creați o coadă goală q
• temp_node = rădăcină /*începe de la rădăcină*/
• Buclă în timp ce temp_node nu este NULL
  • print temp_node->date.
  • Puneți în coadă copiii lui temp_node (în primul rând copiii din stânga apoi din dreapta) la q
  • Scoateți în coadă un nod din q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Imprimați în fața cozii și # eliminați-l din coadă de imprimare (queue[0].data) node = queue.pop(0) # Așezați copilul stânga dacă node.left nu este None: queue.append(node.left ) # Puneți în coadă copilul din dreapta dacă node.right nu este None: queue.append(node.right) # Programul driver de testat deasupra funcției root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Nodul(4) root.left.right = Nodul(5) print ('Ordinea nivelului Traversarea arborelui binar este -') printLevelOrder(rădăcină)>

Level Order Traversal of binary tree is - 1 2 3 4 5>

Complexitatea timpului: O(n)

Mai multe articole despre Arbore binar

• Inserarea într-un arbore binar
• Ștergerea într-un arbore binar
• Traversarea în ordine a copacilor fără recursivitate
• Inorder Tree Traversal fără recursivitate și fără stivă!
• Imprimați parcurgerea Postorder din parcurgerile Inorder și Preorder date
• Găsiți traversarea postcomandă a BST din traversarea precomandă

Arborele de căutare binar este o structură de date arbore binar bazată pe noduri care are următoarele proprietăți:

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)>

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)>

20 30 40 50 60 70 80>

A grafic este o structură de date neliniară constând din noduri și muchii. Nodurile sunt uneori denumite și vârfuri, iar muchiile sunt linii sau arce care conectează oricare două noduri din grafic. Mai formal, un graf poate fi definit ca un graf constând dintr-un set finit de vârfuri (sau noduri) și un set de muchii care conectează o pereche de noduri.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0<=vtx<=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix())>

numerotarea alfabetului

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Program driver la clasa de grafic de mai sus if __name__ == '__main__' : V = 5 graph = Graph(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph()>

Adjacency list of vertex 0 head ->4 -> 1 Lista de adiacență a capului vârfului 1 -> 4 -> 3 -> 2 -> 0 Lista de adiacențe a capului vârfului 2 -> 3 -> 1 Lista de adiacență a capului vârfului 3 -> 4 -> 2 -> 1 Adiacență lista vârfului 4 cap -> 3 -> 1 -> 0>

Traversarea graficului

Breadth-First Search sau BFS

Lățimea-Prima traversare pentru un grafic este similar cu Breadth-First Traversal a unui arbore. Singura captură aici este că, spre deosebire de copaci, graficele pot conține cicluri, așa că putem ajunge din nou la același nod. Pentru a evita procesarea unui nod de mai multe ori, folosim o matrice booleană vizitată. Pentru simplitate, se presupune că toate vârfurile sunt accesibile de la vârful de pornire.

De exemplu, în graficul următor, începem traversarea de la vârful 2. Când ajungem la vârful 0, căutăm toate vârfurile adiacente ale acestuia. 2 este, de asemenea, un vârf adiacent de 0. Dacă nu marchem vârfurile vizitate, atunci 2 va fi procesat din nou și va deveni un proces care nu se încheie. O traversare pe lățime a următorului grafic este 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2)>

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1>

Complexitatea timpului: O(V+E) unde V este numărul de vârfuri din grafic și E este numărul de muchii din grafic.

Depth First Search sau DFS

Adâncimea prima traversare pentru un grafic este similar cu Adâncimea prima traversare a unui arbore. Singura captură aici este, spre deosebire de copaci, graficele pot conține cicluri, un nod poate fi vizitat de două ori. Pentru a evita procesarea unui nod de mai multe ori, utilizați o matrice booleană vizitată.

Algoritm:

• Creați o funcție recursivă care preia indexul nodului și o matrice vizitată.
• Marcați nodul curent ca vizitat și imprimați nodul.
• Traversați toate nodurile adiacente și nemarcate și apelați funcția recursivă cu indexul nodului adiacent.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2)>

Following is DFS from (starting from vertex 2) 2 0 1 3>

Mai multe articole despre grafic

• Reprezentări grafice folosind set și hash
• Găsiți Vertexul Mamă într-un grafic
• Prima căutare iterativă în profunzime
• Numărați numărul de noduri la un anumit nivel dintr-un arbore folosind BFS
• Numărați toate căile posibile între două vârfuri

Procesul în care o funcție se numește direct sau indirect se numește recursie, iar funcția corespunzătoare se numește a functie recursiva . Folosind algoritmii recursivi, anumite probleme pot fi rezolvate destul de usor. Exemple de astfel de probleme sunt Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph etc.

def fact(n):  # base case  if (n <= 1)   return 1  else   return n*fact(n-1)>

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)>

3 2 1 1 2 3>

• Recursiune
• Recursiune în Python
• Întrebări practice pentru recursivitate | Setul 1
• Întrebări practice pentru recursivitate | Setul 2
• Întrebări practice pentru recursivitate | Setul 3
• Întrebări practice pentru recursivitate | Setul 4
• Întrebări practice pentru recursivitate | Setul 5
• Întrebări practice pentru recursivitate | Setul 6
• Întrebări practice pentru recursivitate | Setul 7

>>> Mai multe

Programare dinamică

Programare dinamică este în principal o optimizare asupra recursiunii simple. Oriunde vedem o soluție recursivă care are apeluri repetate pentru aceleași intrări, o putem optimiza folosind programarea dinamică. Ideea este să stocăm pur și simplu rezultatele subproblemelor, astfel încât să nu fie nevoie să le recalculăm atunci când este nevoie mai târziu. Această optimizare simplă reduce complexitatea timpului de la exponențial la polinom. De exemplu, dacă scriem soluții recursive simple pentru numerele Fibonacci, obținem complexitatea timpului exponențial și dacă o optimizăm prin stocarea soluțiilor subproblemelor, complexitatea timpului se reduce la liniară.

Tabulare vs memorare

Există două moduri diferite de a stoca valorile, astfel încât valorile unei sub-probleme să poată fi reutilizate. Aici, vom discuta două modele de rezolvare a problemei de programare dinamică (DP):

• Tabulare: De jos în sus
• Memorare: De sus în jos

Intabulare

După cum sugerează și numele, începeți de jos și acumulând răspunsuri până sus. Să discutăm despre tranziția de stat.

Să descriem o stare pentru problema noastră DP să fie dp[x] cu dp[0] ca stare de bază și dp[n] ca stare de destinație. Deci, trebuie să găsim valoarea stării de destinație, adică dp[n].

Dacă începem tranziția de la starea noastră de bază, adică dp[0] și urmăm relația de tranziție a stării pentru a ajunge la starea de destinație dp[n], o numim abordarea de jos în sus, deoarece este destul de clar că am început tranziția de la starea de bază inferioară și a atins starea cea mai de sus dorită.

Acum, de ce o numim metoda de tabulare?

Pentru a ști acest lucru, să scriem mai întâi un cod pentru a calcula factorialul unui număr folosind abordarea de jos în sus. Încă o dată, ca procedură generală pentru a rezolva un DP, definim mai întâi o stare. În acest caz, definim o stare ca dp[x], unde dp[x] este să găsim factorialul lui x.

Acum, este destul de evident că dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i>

Memorarea

Încă o dată, să o descriem în termeni de tranziție de stat. Dacă trebuie să găsim valoarea unei stări spunem dp[n] și în loc să pornim de la starea de bază, adică dp[0], ne întrebăm răspunsul de la stările care pot ajunge la starea de destinație dp[n] în urma tranziției stării. relație, atunci este moda de sus în jos a DP.

Aici, începem călătoria noastră din starea cea mai de sus de destinație și calculăm răspunsul său luând în calcul valorile stărilor care pot ajunge la starea de destinație, până când ajungem la starea de bază cea mai de jos.

Încă o dată, să scriem codul pentru problema factorială în mod de sus în jos

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1))>

Mai multe articole despre programarea dinamică

• Proprietatea optimă a substructurii
• Proprietatea Subprobleme suprapuse
• numerele Fibonacci
• Submulțime cu suma divizibilă cu m
• Suma maximă în creștere a subsecvenței
• Cel mai lung subșir comun

>>> Mai multe

Algoritmi de căutare

Căutare liniară

• Începeți de la elementul din stânga al lui arr[] și comparați unul câte unul x cu fiecare element al lui arr[]
• Dacă x se potrivește cu un element, returnează indexul.
• Dacă x nu se potrivește cu niciunul dintre elemente, returnați -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result)>

Element is present at index 3>

Complexitatea temporală a algoritmului de mai sus este O(n).

coada de prioritate c++

Pentru mai multe informații, consultați Căutare liniară .

Căutare binară

Căutați o matrice sortată împărțind în mod repetat intervalul de căutare la jumătate. Începeți cu un interval care acoperă întreaga matrice. Dacă valoarea cheii de căutare este mai mică decât elementul din mijlocul intervalului, restrângeți intervalul la jumătatea inferioară. În caz contrar, îngustează-l la jumătatea superioară. Verificați în mod repetat până când este găsită valoarea sau intervalul este gol.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Dacă elementul este prezent la mijloc, dacă arr[mid] == x: return mid # Dacă elementul este mai mic decât mijlocul, atunci poate fi prezent doar # în subbarra stânga elif arr[mid]> x: return binarySearch(arr, l, mid-1, x) # În caz contrar, elementul poate fi prezent numai # în subbarra dreapta else: return binarySearch(arr, mid + 1, r, x ) altfel: # Elementul nu este prezent în matrice returnată -1 # Cod driver arr = [ 2, 3, 4, 10, 40 ] x = 10 # Rezultatul apelului funcției = binarySearch(arr, 0, len(arr)-1 , x) if result != -1: print ('Elementul este prezent la index % d' % result) else: print ('Elementul nu este prezent în matrice')>

Element is present at index 3>

Complexitatea de timp a algoritmului de mai sus este O(log(n)).

Pentru mai multe informații, consultați Căutare binară .

Algoritmi de sortare

Sortare selecție

The sortare de selecție algoritmul sortează o matrice găsind în mod repetat elementul minim (luând în considerare ordinea crescătoare) din partea nesortată și punându-l la început. În fiecare iterație de sortare de selecție, elementul minim (luând în considerare ordinea crescătoare) din subgrupul nesortat este ales și mutat în subbary sortat.

Diagramă de sortare a selecției:

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Schimbați elementul minim găsit cu # primul element A[i], A[min_idx] = A[min_idx], A[i] # Cod driver de testat deasupra tipăririi ('Matrice sortată ') pentru i în interval(len(A)): print('%d' %A[i]),>

Sorted array 11 12 22 25 64>

Complexitatea timpului: Pe²) deoarece există două bucle imbricate.

Spațiu auxiliar: O(1)

Sortare cu bule

Sortare cu bule este cel mai simplu algoritm de sortare care funcționează prin schimbarea în mod repetat a elementelor adiacente dacă acestea sunt în ordine greșită.

Ilustrație:

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Cod driver de testat deasupra arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Matricea sortată este:') pentru i în interval(len(arr)): print ('%d' %arr[i]),>

Sorted array is: 11 12 22 25 34 64 90>

Complexitatea timpului: Pe²)

Sortare prin inserare

Pentru a sorta o matrice de dimensiune n în ordine crescătoare folosind sortare de inserare :

• Iterați de la arr[1] la arr[n] peste matrice.
• Comparați elementul actual (cheia) cu predecesorul său.
• Dacă elementul cheie este mai mic decât predecesorul său, comparați-l cu elementele de dinainte. Mutați elementele mai mari cu o poziție în sus pentru a face spațiu pentru elementul schimbat.

Ilustrare:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 și cheie< arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i])>

 5 6 11 12 13>

Complexitatea timpului: Pe²))

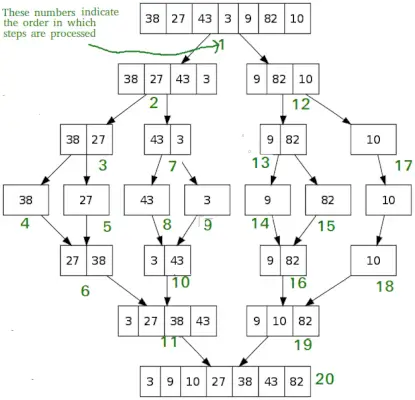
Merge Sort

La fel ca QuickSort, Merge Sort este un algoritm Divide and Conquer. Împarte matricea de intrare în două jumătăți, se numește singur pentru cele două jumătăți și apoi îmbină cele două jumătăți sortate. Funcția merge() este folosită pentru îmbinarea a două jumătăți. Merge(arr, l, m, r) este un proces cheie care presupune că arr[l..m] și arr[m+1..r] sunt sortate și îmbină cele două sub-matrice sortate într-una singură.

MergeSort(arr[], l, r) If r>l 1. Găsiți punctul de mijloc pentru a împărți matricea în două jumătăți: middle m = l+ (r-l)/2 2. Apelați mergeSort pentru prima jumătate: apelați mergeSort(arr, l, m) 3. Apelați mergeSort pentru a doua jumătate: apelați mergeSort(arr, m+1, r) 4. Îmbină cele două jumătăți sortate la pasul 2 și 3: apelează merge(arr, l, m, r)>

# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Găsirea mijlocului matricei mid = len(arr)//2 # Împărțirea elementelor matricei L = arr[:mid] # în 2 jumătăți R = arr[mid:] # Sortarea primei jumătăți mergeSort(L) # Sortarea celei de-a doua jumătăți mergeSort(R) i = j = k = 0 # Copiați datele în matricele temp L[] și R[] în timp ce i< len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr)>

Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13>

Complexitatea timpului: O(n(logn))

Sortare rapida

Ca Merge Sort, Sortare rapida este un algoritm Divide and Conquer. Alege un element ca pivot și partiţionează matricea dată în jurul pivotului ales. Există multe versiuni diferite de quickSort care aleg pivotul în moduri diferite.

Alegeți întotdeauna primul element ca pivot.

• Alegeți întotdeauna ultimul element ca pivot (implementat mai jos)
• Alegeți un element aleatoriu ca pivot.
• Alegeți mediana ca pivot.

Procesul cheie din quickSort este partition(). Ținta partițiilor este, având în vedere un tablou și un element x al matricei ca pivot, puneți x în poziția corectă în matricea sortată și puneți toate elementele mai mici (mai mici decât x) înainte de x și puneți toate elementele mai mari (mai mari decât x) după X. Toate acestea ar trebui făcute în timp liniar.

/* low -->Index de pornire, ridicat --> Index final */ quickSort(arr[], low, high) { if (low { /* pi este index de partiționare, arr[pi] este acum la locul potrivit */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Înainte de pi quickSort(arr, pi + 1, high);
 
 
    Algoritmul de partiție    
 
Pot exista mai multe moduri de a face partiția, urmând  pseudo cod  adoptă metoda dată în cartea CLRS. Logica este simplă, pornim de la elementul din stânga și urmărim indicele elementelor mai mici (sau egale cu) ca i. În timpul traversării, dacă găsim un element mai mic, schimbăm elementul curent cu arr[i]. În caz contrar, ignorăm elementul curent.
  
# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start < end: # Increment the start pointer till it finds an # element greater than pivot while start < len(array) and array[start] <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivot: sfârșit -= 1 # Dacă începutul și sfârșitul nu s-au încrucișat, # schimbați numerele de la început și de la sfârșit if(start< end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}')>
   
  Ieșire  
Sorted array: [1, 5, 7, 8, 9, 10]>
 
    Complexitatea timpului:    O(n(logn))
 
ShellSort
 ShellSort este în principal o variantă a sortării inserției. În sortarea prin inserție, mutăm elementele cu o singură poziție înainte. Când un element trebuie mutat mult înainte, sunt implicate multe mișcări. Ideea shellSort este de a permite schimbul de articole îndepărtate. În shellSort, facem matricea sortată h pentru o valoare mare a h. Continuăm să reducem valoarea lui h până când devine 1. Se spune că o matrice este sortată cu h dacă toate sublistele fiecărei hthelementul este sortat.
Python3 
# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0: i = 0 j = gap # verificați matricea de la stânga la dreapta # până la ultimul index posibil al lui j în timp ce j< len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # acum, ne uităm înapoi de la al-lea index la stânga # schimbăm valorile care nu sunt în ordinea corectă. k = i în timp ce k - decalaj> -1: dacă arr[k - decalaj]> arr[k]: arr[k-gap],arr[k] = arr[k],arr[k-gap] k -= 1 gap //= 2 # driver pentru a verifica codul arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2)>>>  
  Ieșire      Complexitatea timpului:    Pe2).