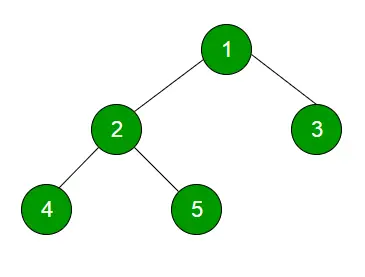
Traversarea ordinului la nivel tehnica este definită ca o metodă de a traversa un Arbore astfel încât toate nodurile prezente în același nivel să fie parcurse complet înainte de a parcurge nivelul următor.

Exemplu:
Parcursul de ordine recomandat la nivel de practică Încercați!Intrare:
Ieșire:
1
23
Patru cinci
Cum funcționează Level Order Traversal?
Ideea principală a traversării ordinii de nivel este de a parcurge toate nodurile unui nivel inferior înainte de a trece la oricare dintre nodurile unui nivel superior. Acest lucru se poate face în oricare dintre următoarele moduri:
- cel naiv (găsirea înălțimii copacului și parcurgerea fiecărui nivel și imprimarea nodurilor acelui nivel)
- folosind eficient o coadă.
Traversarea ordinului la nivel (abordare naivă):
Găsi înălţime de copac. Apoi, pentru fiecare nivel, rulați o funcție recursivă menținând înălțimea curentă. Ori de câte ori nivelul unui nod se potrivește, imprimați acel nod.
Mai jos este implementarea abordării de mai sus:
C++ // Recursive CPP program for level // order traversal of Binary Tree #include using namespace std; // A binary tree node has data, // pointer to left child // and a pointer to right child class node { public: int data; node *left, *right; }; // Function prototypes void printCurrentLevel(node* root, int level); int height(node* node); node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(node* root, int level) { if (root == NULL) return; if (level == 1) cout << root->date<< ' '; else if (level>1) { printCurrentLevel(root->left, level - 1); printCurrentLevel(rădăcină->dreapta, nivel - 1); } } // Calculați 'înălțimea' a unui arbore -- numărul // de noduri de-a lungul celei mai lungi căi de la nodul rădăcină // până la cel mai îndepărtat nod frunză. int inaltime(nodul* nod) { if (nodul == NULL) returneaza 0; else { // Calculați înălțimea fiecărui subarbore int lheight = height(node->left); int rheight = inaltime(nodul->dreapta); // Folosește-l pe cel mai mare if (lheight> rheight) { return (lheight + 1); } else { return (dreapta + 1); } } } // Funcție de ajutor care alocă // un nou nod cu datele date și // pointerii stânga și dreapta NULL. nod* newNode(int data) { nod* Node = nou nod(); Nod->data = date; Nod->stânga = NULL; Nod->dreapta = NULL; return (Nod); } // Cod driver int main() { node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; } // This code is contributed by rathbhupendra> C // Recursive C program for level // order traversal of Binary Tree #include #include // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node *left, *right; }; // Function prototypes void printCurrentLevel(struct node* root, int level); int height(struct node* node); struct node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(struct node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(struct node* root, int level) { if (root == NULL) return; if (level == 1) printf('%d ', root->date); else if (nivel> 1) { printCurrentLevel(rădăcină->stânga, nivel - 1); printCurrentLevel(rădăcină->dreapta, nivel - 1); } } // Calculați 'înălțimea' a unui arbore -- numărul de // noduri de-a lungul celei mai lungi căi de la nodul rădăcină // în jos până la cel mai îndepărtat nod frunză int height(struct node* node) { if (node == NULL) returnează 0; else { // Calculați înălțimea fiecărui subarbore int lheight = height(node->left); int rheight = inaltime(nodul->dreapta); // Folosește-o pe cea mai mare dacă (înălțimea> dreapta) returnează (înălțimea + 1); altfel revenire (dreapta + 1); } } // Funcție de ajutor care alocă un nou nod cu // datele date și indicatori NULL stânga și dreapta. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); nod->data = date; nod->stânga = NULL; nod->dreapta = NULL; returnare (nod); } // Program driver pentru a testa funcțiile de mai sus int main() { struct node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); printf('Parcurgerea ordinului nivelului a arborelui binar este
'); printLevelOrder(rădăcină); întoarce 0; }>>>Javarheight) întoarcere (lheight + 1); altfel revenire (dreapta + 1); } } // Imprimă noduri la nivelul curent void printCurrentLevel(Rădăcină nod, nivel int) { if (rădăcină == null) return; if (nivel == 1) System.out.print(root.data + ' '); else if (nivel> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, level - 1); } } // Program driver pentru a testa funcțiile de mai sus public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = nou Nod(1); tree.root.left = Nod nou (2); tree.root.right = Nod nou (3); tree.root.left.left = Nod nou (4); tree.root.left.right = Nod nou (5); System.out.println('Parcurgerea în ordinea nivelurilor' + 'arborele binar este '); tree.printLevelOrder(); } }>>> Piton1: printCurrentLevel(root.left, level-1) printCurrentLevel(root.right, level-1) # Calculați înălțimea unui copac - numărul de noduri # de-a lungul celei mai lungi căi de la nodul rădăcină în jos până la # cea mai îndepărtată frunză node def height(node): dacă nodul este None: return 0 else: # Calculați înălțimea fiecărui subarbore lheight = height(node.left) rheight = height(node.right) # Folosiți cel mai mare dacă lheight> rheight: return lheight+1 else: return rheight+1 # Program driver pentru a testa funcția de mai sus if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root. left.left = Nodul(4) root.left.right = Nodul(5) print('Parcurgerea în ordinea nivelului a arborelui binar este -') printLevelOrder(rădăcină) # Acest cod este contribuit de Nikhil Kumar Singh(nickzuck_007)> C# // Recursive c# program for level // order traversal of Binary Tree using System; // Class containing left and right // child of current node and key value public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { // Root of the Binary Tree public Node root; public void BinaryTree() { root = null; } // Function to print level order // traversal of tree public virtual void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) { printCurrentLevel(root, i); } } // Compute the 'height' of a tree -- // the number of nodes along the longest // path from the root node down to the // farthest leaf node. public virtual int height(Node root) { if (root == null) { return 0; } else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rheight) { return (lheight + 1); } else { return (dreapta + 1); } } } // Imprimă noduri la nivelul curent public virtual void printCurrentLevel(Rădăcină nod, nivel int) { if (rădăcină == null) { return; } if (nivel == 1) { Console.Write(root.data + ' '); } else if (nivel> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, level - 1); } } // Cod driver public static void Main(string[] args) { GFG tree = new GFG(); tree.root = nou Nod(1); tree.root.left = Nod nou (2); tree.root.right = Nod nou (3); tree.root.left.left = Nod nou (4); tree.root.left.right = Nod nou (5); Console.WriteLine('Parcurgerea ordinului nivelului ' + 'a arborelui binar este '); tree.printLevelOrder(); } } // Acest cod este contribuit de Shrikant13>>Javascriptrheight) întoarcere (lheight + 1); altfel revenire (dreapta + 1); } } // Imprimă noduri la nivelul curent funcția printCurrentLevel(root , level) { if (root == null) return; if (nivel == 1) console.log(root.data + ' '); else if (nivel> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, level - 1); } } // Program driver pentru a testa funcțiile de mai sus root = new Node(1); root.left = nou Nod(2); root.right = nou Nod(3); root.left.left = nou Nod(4); root.left.right = nou Nod(5); console.log('Parcurgerea în ordinea nivelului a arborelui binar este '); printLevelOrder(); // Acest cod este contribuit de umadevi9616>>>
Ieșire Level Order traversal of binary tree is 1 2 3 4 5>
Complexitatea timpului: O(N), unde N este numărul de noduri din arborele înclinat.
Spațiu auxiliar: O(1) Dacă se consideră stiva recursiunii, spațiul folosit este O(N).
cum se transformă șirul în int
Level Order Traversal folosind Coadă
Trebuie să vizităm nodurile de la un nivel inferior înaintea oricărui nod de la un nivel superior, această idee este destul de asemănătoare cu cea a unei cozi. Împingeți nodurile unui nivel inferior în coadă. Când este vizitat orice nod, scoateți acel nod din coadă și împingeți copilul acelui nod în coadă.
Acest lucru asigură că nodul de un nivel inferior este vizitat înainte de orice nod de un nivel superior.
Mai jos este implementarea abordării de mai sus:
C++ // C++ program to print level order traversal #include using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // Iterative method to find height of Binary Tree void printLevelOrder(Node* root) { // Base Case if (root == NULL) return; // Create an empty queue for level order traversal queueq; // Pune la coadă Root și inițializează înălțimea q.push(root); while (q.empty() == false) { // Imprimă în fața cozii și scoate-l din coadă Node* node = q.front(); cout<< node->date<< ' '; q.pop(); // Enqueue left child if (node->stânga != NULL) q.push(nod->stânga); // Pune la coada copilul drept if (nod->right != NULL) q.push(nod->right); } } // Funcție utilitar pentru a crea un nou nod arbore Node* newNode(int data) { Node* temp = new Node; temp->data = date; temp->stânga = temp->dreapta = NULL; temperatura de retur; } // Program driver pentru a testa funcțiile de mai sus int main() { // Să creăm arbore binar prezentat în diagrama de mai sus Node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; }> C // Iterative Queue based C program // to do level order traversal // of Binary Tree #include #include #define MAX_Q_SIZE 500 // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node* left; struct node* right; }; // Function prototypes struct node** createQueue(int*, int*); void enQueue(struct node**, int*, struct node*); struct node* deQueue(struct node**, int*); // Given a binary tree, print its nodes in level order // using array for implementing queue void printLevelOrder(struct node* root) { int rear, front; struct node** queue = createQueue(&front, &rear); struct node* temp_node = root; while (temp_node) { printf('%d ', temp_node->date); // Așezați copilul stânga if (temp_node->left) enQueue(queue, &rear, temp_node->left); // Pune în coadă copilul drept if (temp_node->right) enQueue(queue, &rear, temp_node->right); // Scoateți la coadă nodul și faceți-l temp_node temp_node = deQueue(coadă, &front); } } // Funcții utilitare struct node** createQueue(int* front, int* rear) { struct node** coada = (struct node**)malloc( sizeof(struct node*) * MAX_Q_SIZE); *fata = *spate = 0; coada de returnare; } void enQueue(struct node** coada, int* rear, struct node* new_node) { coada[*spate] = new_node; (*spate)++; } struct node* deQueue(struct node** coada, int* front) { (*front)++; coada de returnare[*front - 1]; } // Funcție de ajutor care alocă un nou nod cu // datele date și pointerii stânga și dreapta NULL. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); nod->data = date; nod->stânga = NULL; nod->dreapta = NULL; returnare (nod); } // Program driver pentru a testa funcțiile de mai sus int main() { struct node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); printf('Parcurgerea ordinului nivelului a arborelui binar este
'); printLevelOrder(rădăcină); întoarce 0; }>>>Java>> Piton C# // Iterative Queue based C# program // to do level order traversal // of Binary Tree using System; using System.Collections.Generic; // Class to represent Tree node public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal public class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order using // array for implementing queue void printLevelOrder() { Queuecoadă = coadă nouă(); queue.Enqueue(rădăcină); while (coadă.Număr != 0) { Node tempNode = coadă.Decodă (); Console.Write(tempNode.data + ' '); // Pune la coadă copilul stâng dacă (tempNode.left != null) { queue.Enqueue(tempNode.left); } // Pune în coadă copilul drept dacă (tempNode.right != null) { queue.Enqueue(tempNode.right); } } } // Cod driver public static void Main() { // Crearea unui arbore binar și introducerea // nodurile BinaryTree tree_level = new BinaryTree(); tree_level.root = nou Node(1); tree_level.root.left = nou Nod(2); tree_level.root.right = Nod nou (3); tree_level.root.left.left = nou Nod(4); tree_level.root.left.right = Nod nou (5); Console.WriteLine('Parcurgerea ordinului nivelului ' + 'a arborelui binar este - '); tree_level.printLevelOrder(); } } // Acest cod a contribuit de PrinciRaj1992>>Javascript Ieșire
Spațiu auxiliar: O(N) unde N este numărul de noduri din arborele binar.