Trigonometria este o ramură importantă a matematicii care se ocupă de relația dintre unghiurile și lungimile laturilor unui triunghi dreptunghic. Cele șase rapoarte sau funcții trigonometrice sunt sinus, cosinus, tangentă, cosecantă și secanta, iar un raport trigonometric este un raport între laturile unui triunghi dreptunghic. Funcțiile sinus, cosinus și tangentă sunt trei funcții trigonometrice importante, deoarece celelalte trei, adică funcțiile cosecante, secante și cotangente sunt funcțiile reciproce ale funcțiilor sinus, cosinus și, respectiv, tangentă.
- sin θ = Latura opusă/ipotenuză
- cos θ = Latura adiacentă/Hipotenuză
- tan θ = Latura opusă/Latura adiacentă
- cosec θ = Hipotenuză/Latura opusă
- sec θ = Hipotenuză/Latura adiacentă
- cot θ = Latura adiacentă/Latura opusă
Funcția tangentă este una dintre cele 6 funcții trigonometrice utilizate în formule de trigonometrie .
Cuprins
Formula tangentă
Tangenta unui unghi dintr-un triunghi dreptunghic este raportul dintre lungimea laturii opuse și lungimea laturii adiacente unghiului dat. Scriem o funcție tangentă ca tan. Să considerăm un triunghi dreptunghic XYZ și unul dintre unghiurile sale ascuțite este θ. O latură opusă este latura opusă unghiului θ, iar latura adiacentă este latura adiacentă unghiului θ.
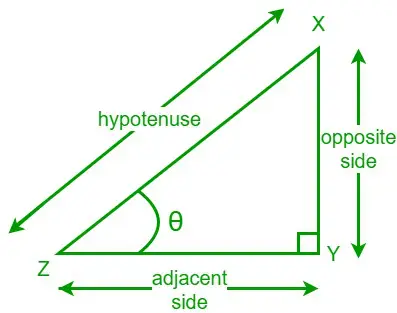
Acum, formula tangentei pentru unghiul dat θ este,
tan θ = Latura opusă/Latura adiacentă
Câteva formule tangente de bază
Funcția tangentă în cadrane
Funcția tangentă este pozitivă în primul și al treilea cadran și negativă în al doilea și al patrulea cadran.
- tan (2π + θ) = tan θ (1Sfcadran)
- tan (π – θ) = – tan θ (2ndcadran)
- tan (π + θ) = tan θ (3rdcadran)
- tan (2π – θ) = – tan θ (4thcadran)
Funcția tangentă ca funcție negativă
Funcția tangentă este o funcție negativă, deoarece tangenta unui unghi negativ este negativul unui unghi tangentă pozitiv.
tan (-θ) = – tan θ
Funcția tangentă în termeni de funcție sinus și cosinus
Funcția tangentă în termeni de funcții sinus și cosinus poate fi scrisă ca,
tan θ = sin θ/cos θ
Știm că, tan θ = Latura opusă/Latura adiacentă
Acum, împărțiți atât numărătorul, cât și numitorul cu ipotenuza
tan θ = (Latura opusă/Hipotenuză)/(Latura adiacentă/Hipotenuză)
Știm că, sin θ = latura opusă/ipotenuză
cos θ = latura adiacentă/ipotenuză
Prin urmare, tan θ = sin θ/cos θ
Funcția tangentă în termeni de funcție sinusoidală
Funcția tangentă în termenii funcției sinus poate fi scrisă ca,
tan θ = sin θ/(√1 – sin 2 i)
Noi stim aia,
tan θ = sin θ/cos θ
topologie în stea
Din identitățile pitagoreice, avem,
fără2θ + cos2θ = 1
cos2θ = 1 – sin2i
cos θ = √(1 – sin2i)
Prin urmare, tan θ = sin θ/(√1 – sin2i)
Funcția tangentă în termeni de funcție cosinus
Funcția tangentă în termenii funcției cosinus poate fi scrisă ca,
tan θ = (√1 -cos 2 i)/cos i
Noi stim aia,
tan θ = sin θ/cos θ
Din identitățile pitagoreice, avem,
fără2θ + cos2θ = 1
fără2θ = 1 – cos2i
sin θ = √(1 – cos2i)
Prin urmare, tan θ = (√1 – cos2i)/cos i
Funcția tangentă în termeni de funcție cotangentă
Funcția tangentă în termenii funcției cotangente poate fi scrisă ca,
tan θ = 1/cot θ
sau
tan θ = cot (90° – θ) (sau) cot (π/2 – θ)
Funcția tangentă în termeni de funcție cosecantă
Funcția tangentă în termenii funcției cosecante poate fi scrisă ca,
tan θ = 1/√(cosec 2 i – 1)
Din identitățile pitagoreice, avem,
cosec2θ – pătuț2θ = 1
pat2θ = cosec2eu – 1
cot θ = √(cosec2i – 1)
Noi stim aia,
tan θ = 1/cot θ
Prin urmare, tan θ = 1/√(cosec2i – 1)
Funcția tangentă în termeni de funcție secante
Funcția tangentă în termenii funcției secante poate fi scrisă ca,
tan θ = √sec 2 eu – 1
Din identitățile pitagoreice, avem,
sec2θ – deci2θ = 1
tan θ = sec2eu – 1
Prin urmare, tan θ = √(sec2i – 1)
Funcția tangentă în termeni de unghi dublu
Funcția tangentă pentru un unghi dublu este,
tan 2θ = (2 tan θ)/(1 – tan 2 i)
Funcția tangentă în termeni de unghi triplu
Funcția tangentă pentru un unghi triplu este,
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 tan 2 i)
Funcția tangentă în termeni de semiunghi
Funcția tangentă pentru un semiunghi este,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Funcția tangentă în termeni de adunare și scădere a două unghiuri
Formulele de sumă și diferență pentru o funcție tangentă sunt:
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Tabelul cu rapoarte trigonometrice
| Unghi (în grade) | Unghi (în radiani) | păcatul i | cos θ | tan θ = sin θ/cos θ | cosec θ | sec θ | pat i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Nedefinit | 1 | Nedefinit |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 subșir de tăiere javascript | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = nedefinit | 1 | Nedefinit | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Nedefinit | -1 | Nedefinit |
Exemplu rezolvat pe formule tangente
Exemplul 1: Aflați valoarea lui tan θ dacă sin θ = 2/5 și θ este primul unghi de cadran.
Soluţie:
Dat,
- sin θ = 2/5
Din identitățile pitagorice pe care le avem,
fără2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Deoarece θ este primul unghi de cadran, cos θ este pozitiv.
cos θ = √21/5
Noi stim aia,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21 /21
Deci, valoarea lui tan θ când sin θ = 2/5 și θ este în primul cadran este (2√21) /(21)
Exemplul 2: Aflați valoarea lui tan x dacă sec x = 13/12 și x este al patrulea unghi cadran.
Soluţie:
Având în vedere, sec x = 13/12
Din identitățile pitagoreice, avem,
sec2x – deci2x = 1
asa de2x = sec2x – 1= (13/12)2- 1
asa de2x = (169/144) – 1= 25/144
tan x = ± 5/12
Deoarece x este al patrulea unghi cadran, tan x este negativ.
tan x = – 5/12
Prin urmare, tan x = – 5/12
Exemplul 3: Dacă tan X = 2/3 și tan Y = 1/2, atunci care este valoarea tan (X + Y)?
Soluţie:
Dat,
tan X = 2/3 și tan Y = 1/2
Noi stim aia,
caracter java în șirtan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
bronz (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Prin urmare, tan(X + Y) = 7/4
Exemplul 4: Calculați funcția tangentă dacă laturile adiacente și opuse ale unui triunghi dreptunghic au 4 cm și, respectiv, 7 cm.
Soluţie:
Dat,
Latura adiacentă = 4 cm
Partea opusă = 7 cm
Noi stim aia,
tan θ = Latura opusă/Latura adiacentă
tan θ = 7/4 = 1,75
Prin urmare, tan θ = 1,75
Exemplul 5: Un bărbat se uită la un turn cu ceas la un unghi de 60° față de vârful turnului, a cărui înălțime este de 100 m. Care este distanța dintre om și piciorul turnului?
Soluţie:
Dat,
Înălțimea turnului = 100 m și θ = 60°
Fie distanța dintre om și piciorul turnului = d
Avem,
tan θ = Latura opusă/Latura adiacentă
tan 60° = 100/d
√3 = 100/d [Deoarece, deci 60° = √3]
d = 100/√3
Prin urmare, distanța dintre om și piciorul turnului este 100/√3
Exemplul 6: Aflați valoarea lui tan θ dacă sin θ = 7/25 și sec θ = 25/24.
Soluţie:
Dat,
sin θ = 7/25
sec θ = 25/24
Noi stim aia,
sec θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Avem,
tan θ = sin θ/cos θ
= (25/7)/(24/25)
= 7/24
Prin urmare, tan θ = 7/24
Exemplul 7: Aflați valoarea lui tan θ dacă cosec θ = 5/3 și θ este primul unghi de cadran.
Soluţie:
Dat, cosec θ = 5/3
Din identitățile pitagoreice, avem,
123filmcosec2θ – pătuț2θ = 1
pat2θ = cosec2eu – 1
pat θ = (5/3)2– 1 = (25/9) – 1 = 16/9
cot θ = ±√16/9 = ± 4/3
Deoarece θ este primul unghi de cadran, atât funcțiile cotangente cât și cele tangente sunt pozitive.
pat θ = 4/3
Noi stim aia,
cot θ = 1/tan θ
4/3 = 1/tanθ
tan θ = 3/4
Prin urmare, tan θ = 3/4
Exemplul 8: Găsiți tan 3θ dacă sin θ = 3/7 și θ este primul unghi de cadran.
Solutie:
Dat, sin θ = 12/13
Din identitățile pitagorice pe care le avem,
fără2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Deoarece θ este primul unghi de cadran, cos θ este pozitiv.
cos θ = 5/13
Noi stim aia,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Prin urmare, tan θ = 12/5
Acum, știm că,
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

