Formule Sin Cos în trigonometrie: Trigonometria, după cum sugerează și numele, este studiul triunghiurilor. Este o ramură importantă a matematicii care studiază relația dintre lungimile laturilor și unghiurile triunghiului dreptunghic și, de asemenea, ajută la determinarea lungimii laturilor sau unghiurilor lipsă ale unui triunghi. Există șase rapoarte sau funcții trigonometrice: sinus, cosinus, tangent, cosecant, secant și cotangent, unde cosecant, secant și cotangent sunt funcțiile reciproce ale celorlalte trei funcții, adică sinus, cosinus și, respectiv, tangente.
Un raport trigonometric este definit ca raportul dintre lungimile laturilor unui triunghi dreptunghic. Trigonometria este folosită în diverse domenii din viața noastră de zi cu zi. Ajută la determinarea înălțimii dealurilor sau clădirilor. Este, de asemenea, utilizat în domenii precum criminologie, construcții, fizică, arheologie, inginerie a motoarelor marine etc.
În acest articol, le vom explora pe toate formule de trigonometrie în principal formule sin și cos cu exemplele lor și o listă a tuturor formulelor din trigonometrie.
Cuprins
- Formule în trigonometrie
- Câteva formule de bază Sin Cos
- Sin Cos Formule Tabel
- Sin Cos Formule Exemple
- Practicați probleme pe formule Sin Cos în trigonometrie cu exemple
Formule în trigonometrie
Să considerăm un triunghi dreptunghic XYZ, unde ∠Y = 90°. Fie unghiul de la vârful Z θ. Latura adiacentă lui θ se numește latura adiacentă, iar latura opusă lui θ se numește latura opusă. O ipotenuză este o latură opusă unghiului drept sau cea mai lungă latură a unui unghi drept.
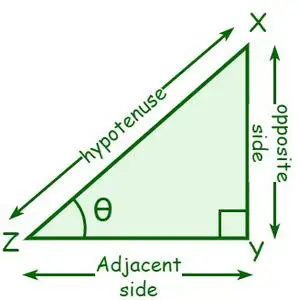
- sin θ = Latura opusă/ipotenuză
- cos θ = Latura adiacentă/Hipotenuză
- tan θ = Latura opusă/Latura adiacentă
- cosec θ = 1/sin θ = Hipotenuză/Latura opusă
- sec θ = 1/ cos θ = Hipotenuză/Latura adiacentă
- cot θ = 1/ tan θ = Latura adiacentă/Latura opusă
Formula Sinusului
Sinusul unui unghi dintr-un triunghi dreptunghic este raportul dintre lungimea laturii opuse și lungimea ipotenuzei la unghiul dat. O funcție sinus este reprezentată ca sin.
sin θ = Latura opusă/ipotenuză
Formula cosinus
Cosinusul unui unghi dintr-un triunghi dreptunghic este raportul dintre lungimea laturii adiacente și lungimea ipotenuzei la unghiul dat. O funcție cosinus este reprezentată ca cos.
piton de inserarecos θ = Latura adiacentă/Hipotenuză
Câteva formule de bază Sin Cos
Funcții sinus și cosinus în cadrane
- Funcția sinus este pozitivă în primul și al doilea cadran și negativă în al treilea și al patrulea cadran.
- Funcția cosinus este pozitivă în primul și al patrulea cadran și negativă în al doilea și al treilea cadran.
Grade
Cuadrant
Semnul funcției Sine
Semnul funcției Cosinus
0° până la 90°
cadranul 1
+ (pozitiv)
+ (pozitiv)
90° până la 180°
al 2-lea cadran
+ (pozitiv)
– (negativ)
180° până la 270°
al 3-lea cadran
– (negativ)
– (negativ)
270° până la 360°
al 4-lea cadran
– (negativ)
+ (pozitiv)
Identitatea unghiului negativ al funcțiilor sinus și cosinus
- Sinusul unui unghi negativ este întotdeauna egal cu sinusul negativ al unghiului.
sin (– θ) = – sin θ
- Cosinusul unghiului negativ este întotdeauna egal cu cosinusul unghiului.
cos (– θ) = cos θ
Relația dintre funcția sinus și cosinus
sin θ = cos (90° – θ)
Funcții reciproce ale funcțiilor sinus și cosinus
- O funcție Cosecantă este funcția reciprocă a funcției sinus.
cosec θ = 1/sin θ
- O funcție Secantă este funcția reciprocă a funcției cosinus.
sec θ = 1/cos θ
identitate pitagoreică
fără 2 θ + cos 2 θ = 1
Identităţi periodice ale funcţiilor sinus şi cosinus
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Formule cu unghi dublu pentru funcțiile sinus și cosinus
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – păcat 2 θ = 2 cos 2 θ – 1 = 1 – 2 sin 2 i
Identități de semiunghi pentru funcțiile sinus și cosinus
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Identități de unghi triplu pentru funcțiile sinus și cosinus
sin 3θ = 3 sin θ – 4 sin 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Formule de sumă și diferență
- Funcția sinusoidală
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- Funcția cosinus
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Legea sinusurilor sau regula sinusurilor
Legea sinusurilor regula sinusurilor este o lege trigonometrică care dă o relație între lungimile laturilor și unghiurile unui triunghi.

a/sin A = b/sin B = c/sin C
Unde a, b și c sunt lungimile celor trei laturi ale triunghiului ABC, iar A, B și C sunt unghiurile.
Legea cosinusurilor
Legea cosinusului regulii cosinusului este folosită pentru a determina unghiurile lipsă sau necunoscute sau lungimile laturilor unui triunghi.

A 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Unde a, b și c sunt lungimile celor trei laturi ale triunghiului ABC, iar A, B și C sunt unghiurile.
Sin Cos Formule Tabel
Iată tabelul/lista cu formule Sin și Cos pentru diferite unghiuri în grade și în radiani:
Lista de formule Sin Cos
| Unghi (în grade) | Unghi (în radiani) | păcatul i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Sin Cos Formule Exemple
Problema 1: Dacă cos α = 24/25, atunci găsiți valoarea sin α.
Soluţie:
Dat,
cos α = 24/25
Din identitățile pitagoreice avem;
cos2θ + sin2θ = 1
(24/25)2+ fără2α = 1
fără2α = 1 – (24/25)2
fără2α = 1 – (576/625) = (625 – 576)/625
fără2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Prin urmare, sin α = ±7/25.
Problema 2: Demonstrați formulele sin 2A și cos 2A, dacă ∠A= 30°.
Soluţie:
Având în vedere, ∠A= 30°
Noi stim aia,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Deoarece, sin 30° = 1/2, cos 30° = √3/2 și sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Deoarece, cos 60° = 1/2 și cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Prin urmare dovedit.
Problema 3: Aflați valoarea lui cos x, dacă tan x = 3/4.
Soluţie:
Dat, tan x = 3/4
Noi stim aia,
tan x = latura opusă/latura adiacentă = 3/4
Pentru a găsi ipotenuza, folosim teorema lui Pitagora:
ipotenuză2= opus2+ adiacent2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Acum, cos x = latura adiacentă/ipotenuză
cos x = 4/5
Astfel, valoarea lui cos x este 4/5.
Problema 4: Aflați ∠C (în grade) și ∠A (în grade), dacă ∠B = 45°, BC = 15 in și AC = 12 in.

Soluţie:
Dat fiind: ∠B = 45°, BC = a = 15 in, și AC = b = 12 in.
Din legea sinusurilor, avem
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ fără A = 15/16,97 = 0,8839
⇒ ∠A = sin-1(0,8839) = 62,11°
Știm că suma unghiurilor interioare ale unui triunghi este de 180°.
Deci, ∠A + ∠B + ∠C = 180°
mysql arată toți utilizatorii⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Prin urmare, ∠A = 62,11° și ∠C = 72,89°.
Problema 5: Demonstrați identitățile semiunghiului ale funcției cosinus.
Soluţie:
Identitatea semiunghiului a funcției cosinus este:
cos (θ/2) = ±√[(1 + cos θ)/2]
Din identitățile cu unghi dublu, avem,
cos 2A = 2 cos2A – 1
Acum înlocuiți A cu θ/2 pe ambele părți
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Prin urmare dovedit.
Practicați probleme pe formule Sin Cos în trigonometrie cu exemple
1. Având în vedere sin θ = 3/5. Găsiți cos θ.
2. Demonstrați identitatea sin(2A) = 2 sinA cosA pentru A=45∘.
3. Dacă cos α = 5/13. Găsiți păcatul(2a).
4. Rezolvați pentru θ dacă sin θ = cos(90∘−θ).
5. Dacă tan β = 2. Aflați sin β și cos β folosind identitatea pitagoreică.
Întrebări frecvente despre formulele Sin Cos în trigonometrie cu exemple
Care sunt formulele de bază sinus și cosinus în trigonometrie?
Formulele de bază ale sinusului și cosinusului sunt sin θ = Opus/Hipotenuză și cos θ = Adiacent/Hipotenuză, unde θ este un unghi într-un triunghi dreptunghic.
Cum găsești sinusul și cosinusul unghiurilor speciale?
Unghiurile speciale, cum ar fi 0∘, 30∘, 45∘, 60∘ și 90∘ au valori specifice de sinus și cosinus care pot fi reținute folosind tabele trigonometrice sau concepte de cerc unitar.
Care este relația dintre funcțiile sinus și cosinus?
Funcțiile sinus și cosinus sunt legate prin identitate sin θ = cos(90∘- θ) și identitatea pitagoreică fără 2 θ+cos 2 θ = 1.
Cum folosiți formulele cu unghi dublu pentru sinus și cosinus?
Formulele unghiului dublu sunt sin(2θ) = 2sinθcosθ și cos(2θ)=cos 2 θ – sin 2 i. Acestea sunt folosite pentru a exprima funcțiile trigonometrice ale unghiurilor duble în termeni de unghiuri simple.
Cum găsiți valorile sinusului și cosinusului pentru unghiuri din diferite cadrane?
Semnele funcțiilor sinus și cosinus depind de cadranul în care se află unghiul:
- Primul cadran: sin θ> 0 și cos θ> 0
- Al doilea cadran: sin θ> 0 și cos θ <0
- Al treilea cadran: sinθ <0 și cosθ <0
- Al patrulea cadran: sinθ 0
