Poligon în matematică este o formă bidimensională alcătuită din linii drepte care formează un lanț poligonal închis. Cuvântul poligon provine din cuvintele poli și gon, care înseamnă multe și laturi.
Poligoanele pot fi simple sau auto-intersectate. Un poligon simplu nu se intersectează, cu excepția punctelor finale comune ale segmentelor consecutive. Un lanț poligonal care se încrucișează pe sine creează un poligon care se intersectează. Poligoanele pot fi, de asemenea, clasificate ca concave sau convexe.
În acest articol, am menționat în detaliu despre poligoane și tipurile, formulele și exemplele acestora.
| Fapte importante despre poligoane | |
|---|---|
| Suma unghiurilor interioare ale poligonului | (n–2) × 180° |
| Numărul de diagonale din poligon | n(n–3)/2 |
| Unghiul interior al poligonului obișnuit | {(n–2) × 180°}/n |
| Unghiul exterior al poligonului regulat | 360°/n |
Cuprins
- Ce sunt poligoanele?
- Diagrama poligonală bazată pe numărul de laturi
- Proprietățile poligoanelor
- Forme de poligon
- Tipuri de poligoane
- Formule poligonale
- Unghiuri în poligoane
- Întrebări frecvente
Ce sunt poligoanele?
Termenul „Poligon” provine din cuvântul grecesc polugonos, unde „poli” înseamnă „mulți”, iar „gon” înseamnă „unghi”. În general, un poligon este o figură închisă formată din linii drepte, cu unghiurile sale interioare create de acestea linii. Pentru a constitui o formă închisă, este necesar un minim de trei segmente de linii. Este cunoscut în mod obișnuit ca triunghi sau 3-gon. Termenul general pentru un poligon cu n laturi este un n-gon.
Definiția poligonului
Poligoane sunt figuri plate, bidimensionale, compuse din laturi drepte care formează o formă complet închisă. În geometrie, poligonul este o figură plană formată din segmente de linie conectate pentru a forma un lanț poligonal închis. Ele constau din laturi drepte, nu curbe și pot avea orice număr variabil de laturi. Unele poligoane de diferite tipuri sunt: deschise, numai de frontieră, închise și auto-intersectante.
În geometrie, un poligon este definit ca o formă închisă, bidimensională, care se află plat într-un plan și este închisă de laturi drepte.
Un poligon nu are laturile curbe, iar marginile sale sunt segmentele drepte care îi definesc granița. Punctele de întâlnire ale acestor muchii sunt denumite vârfuri sau colțuri.
Exemple de poligoane
În ceea ce privește matematica, triunghiurile, hexagoanele, pentagoanele și patrulaterele sunt exemple de poligoane. Exemple reale de Polygon sunt ecranul în formă dreptunghiulară de pe laptop, televizor, telefon mobil; teren dreptunghiular de fotbal sau loc de joacă, Triunghiul Bermudelor și Piramidele Egiptului de formă triunghiulară.

Părți ale unui poligon
Un poligon cuprinde trei componente fundamentale:
- Laturile poligonului: Laturile unui poligoane sunt limita poligoanelor care definesc regiunea închisă.
- vârfuri: Punctul în care două laturi se întâlnesc este cunoscut sub numele de vârf.
- Unghiuri: Poligonul conține atât unghiuri interioare, cât și unghiuri exterioare. Un unghi interior se formează în regiunea închisă a poligonului prin intersecția laturilor sale.
Diagrama poligonală bazată pe numărul de laturi
Nomenclatura poligonului definită pe baza numărului de laturi pe care le posedă. Este desemnat ca n-goni, unde „n” înseamnă numărul de laturi. Poligoanele sunt în general identificate după cantitatea marginilor lor. De exemplu, un poligon cu cinci laturi este denumit 5-gon, în timp ce unul cu zece laturi este denumit 10-gon.
| Diagrama poligonală | ||||
|---|---|---|---|---|
| Nume de formă de poligon | Numărul de laturi | Numărul de vârfuri | Numărul de diagonale | Măsurarea unghiului interior pentru formă obișnuită |
| Triunghi | Poligoane cu 3 laturi | 3 | 0 | 60° |
| Patrulater cel mai bun hentai | Poligoane cu 4 laturi | 4 | 2 | 90° |
| Pentagon | Poligoane cu 5 laturi | 5 | 5 | 108° |
| Hexagon | Poligoane cu 6 laturi | 6 | 9 | 120° |
| Heptagon | Poligoane cu 7 laturi | 7 | 14 | 128,571° |
| Octogon | Poligoane cu 8 laturi | 8 | douăzeci | 135° |
| Nonagon | Poligoane cu 9 laturi | 9 | 27 | 140° transformă șirul în int |
| Decagon | Poligoane cu 10 laturi | 10 | 35 | 144° |
| Hendecagon | Poligoane cu 11 laturi | unsprezece | 44 | 147,273° |
| Dodecagonul | Poligoane cu 12 laturi | 12 | 54 | 150° |
Proprietățile poligoanelor
Proprietățile poligoanelor le identifică cu ușurință. Următoarele proprietăți contribuie la cunoașterea cu ușurință a poligoanelor:
- Un poligon este o formă închisă, lipsită de capete deschise. Originea și punctul final ar trebui să fie aceleași.
- Acesta presupune o formă plană, constând din segmente de linie sau linii drepte care modelează colectiv figura.
- Ca entitate bidimensională, un poligon există doar în dimensiunile de lungime și lățime, lipsit de adâncime sau înălțime.
- Are trei sau mai multe laturi pentru a face un poligon.
- Unghiurile din poligon pot varia. Prezintă configurație distinctă.
- Lungimea laturilor unui poligon poate varia; poate fi sau nu egal în poligon.
Forme de poligon
Un poligon este o formă plată, bidimensională, caracterizată prin laturi drepte conectate pentru a forma o figură închisă. Exemple de forme de poligon includ:
- Triunghi
- Patrulater
- Pentagon
- Hexagon
- Heptagon
- Octogon
- Nonagon
- Decagon
Triunghi
- Are 3 laturi și 3 vârfuri.
- Nu are diagonale.
- Suma interiorului este de 180°.
Patrulater
- Are 4 laturi și 4 vârfuri.
- Are 2 diagonale.
- Suma unghiului interior este 360°.
Pentagon
- Are 5 laturi și 5 vârfuri.
- Are 5 diagonale.
- Suma unghiului interior este 540°.
Hexagon
- Are 6 laturi și 6 vârfuri.
- Are 9 diagonale.
- Suma unghiului interior este 720°.
Heptagon
- Are 7 laturi și 7 vârfuri.
- Are 14 diagonale.
- Suma unghiului interior este de 900°.
Octogon
- Are 8 laturi și 8 vârfuri.
- Are 20 de diagonale.
- Suma unghiului interior este 1080°.
Nonagon
- Are 9 laturi și 9 vârfuri.
- Are 27 de diagonale.
- Suma unghiului interior este 1260°.
Decagon
- Are 10 laturi și 10 vârfuri.
- Are 35 de diagonale.
- Suma unghiului interior este 1440°.
Tipuri de poligoane
În funcție de laturi și unghiuri, poligoanele pot fi clasificate în diferite tipuri pe diferite baze, cum ar fi:
- Pe Baza Laturilor
- Pe baza unghiurilor
- Pe baza limitei
Poligoane pe baza laturilor
Poligoanele pot fi clasificate în funcție de caracteristicile laturilor lor în două tipuri principale:
- Poligon regulat
- Poligon neregulat
Poligon regulat
Un poligon regulat se distinge prin faptul că are toate laturile de lungime egală și toate unghiurile interioare cu măsurători egale. Poate fi atât echilateral, cât și echiunghiular. Exemple de poligoane regulate includ triunghiul, patrulaterul, pentagonul și hexagonul.

Poligon regulat
Poligon neregulat
Un poligon neregulat are laturi de lungime inegală și unghiuri de măsuri diferite. Orice poligon care nu corespunde criteriilor unui poligon regulat este clasificat ca neregulat. Exemple comune de poligon neregulat sunt triunghiul scalen, patrulatere precum dreptunghi, trapez sau zmeu, precum și structuri neregulate pentagon și hexagonale.
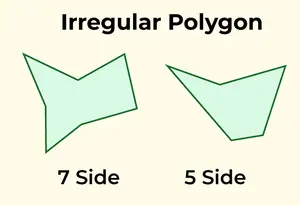
Poligon neregulat
Poligoane pe baza unghiurilor
Poligoanele pot fi clasificate în funcție de natura unghiurilor lor în două categorii principale:
- Poligon convex
- Poligon concav
Poligon convex
Un poligon convex nu are unghi interior care să măsoare mai mult de 180°. Poligoanele convexe pot avea trei sau mai multe laturi. În poligoane convexe, toate diagonalele se află în interiorul figurii închise. Exemple obișnuite de poligoane convexe sunt triunghiurile, toate patrulaterele convexe, precum și pentagoanele și hexagoanele regulate.
Poligon concav
Un poligon concav are cel puțin un unghi interior care este un unghi reflex și este îndreptat spre interior. Poligoanele concave au cel puțin patru laturi. Acest tip de poligon are cel puțin un unghi interior care măsoară mai mult de 180°. În poligoane concave, unele diagonale se extind în afara figurii incluse. Exemplele de poligoane concave includ un dart sau un vârf de săgeată în patrulatere, precum și anumite pentagoane și hexagoane neregulate.
Diferența dintre poligoane concave și convexe
Să vedem diferența dintre poligonul convex și concav în tabelul de mai jos:

| Poligon convex | Poligon concav |
|---|---|
| Întregul perimetru al unei forme convexe se extinde spre exterior, fără adâncituri spre interior. | O formă concavă prezintă cel puțin o porțiune îndreptată spre interior, indicând prezența unei adâncituri. |
| Într-un poligon convex, toate unghiurile interne sunt sub 180°. | Într-un poligon concav, există cel puțin un unghi interior care depășește 180°. |
| Orice linie care leagă două vârfuri ale unei forme convexe se află în întregime în limitele formei. | Linia care leagă oricare două vârfuri ale unei forme concave poate sau nu să intersecteze interiorul formei. |
Poligoane pe bază de limite
Poligoanele pot fi clasificate în funcție de natura limitelor lor în două tipuri principale:
- Poligon simplu
- Poligon complex
Poligon simplu
Un poligon simplu este caracterizat printr-o limită singulară, care nu se intersectează. Cu alte cuvinte, nu se încrucișează și constă dintr-o singură limită.
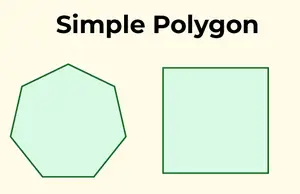
Poligoane simple
Poligon complex
Pe de altă parte, un poligon complex este definit de intersectarea în sine. Constă din mai mult de o graniță în structura sa. În poligoane complexe, granița se intersectează, creând mai multe regiuni distincte în poligon.

Poligon complex
Citiți mai multe despre Tipuri de poligoane.
Formule poligonale
Există mai multe formule legate de poligoane în geometrie. Unele dintre cele mai frecvent utilizate includ:
- Formula zonei
- Formula perimetrului
- Numărul de diagonale
Toate formulele legate de diferite poligoane sunt discutate mai jos:
Zona poligoanelor
Aria unui poligon reprezintă spațiul total pe care îl ocupă într-un plan bidimensional, este determinat de formule specifice bazate pe numărul de laturi și clasificarea poligonului. Formulele zonei sunt următoarele:
| Zona poligonului | Formulă |
|---|---|
| Aria triunghiului | 1/2 × bază × înălțime |
| Aria paralelogramului | Bază × Înălțime Wolverine vs Bursucul |
| Aria unui dreptunghi | Lungime × lățime |
| Suprafața pieței | (Latură)2 |
| 1/2 × diagonală1× diagonală2 | |
| Zona Trapezului | 1/2 × Înălțime × Suma laturilor paralele |
| (5/2) × lungimea laturii × Apotema | |
| Zona hexagonului | {(3√3)/2}partea2 |
| Zona Heptagonului | 3.643 × Latură2 |
Perimetrul poligoanelor
Perimetrul unei forme bidimensionale reprezintă lungimea totală a limitei sale exterioare. Pentru poligoane, perimetrul se calculează după cum urmează:
| Perimetrul poligonului | Formulă |
|---|---|
| Perimetrul triunghiului | Suma celor trei laturi |
| Perimetrul paralelogramului dezinstalați unghiular cli | 2 (Suma laturilor adiacente) |
| Perimetrul dreptunghiului | 2 (lungime + latime) |
| Perimetrul pătratului | 4 × lateral |
| Perimetrul rombului | 4 × lateral |
| Perimetrul Trapezului | Suma laturilor paralele + Suma laturilor neparalele |
| Perimetrul Pentagonului | 5 × lateral |
| Perimetrul hexagonului | 6 × lateral |
| Perimetrul Heptagonului | 7 × lateral |
Diagonala poligonului Formula
O diagonală a unui poligon este un segment de linie format prin conectarea a două vârfuri care nu sunt adiacente.
Numărul de diagonale dintr-un poligon = n(n−3)/2,
Unde „n” reprezintă numărul de laturi pe care le posedă poligonul.
Citiți mai multe despre Diagonala poligonului Formula .
Unghiuri în poligoane
În geometrie, unghiurile în poligoane se referă la unghiurile formate de laturile unui poligon, atât în interiorul, cât și în exteriorul poligonului. Astfel, pot exista ambele unghiuri în poligon, adică,
- Unghiuri interioare
- Unghiuri exterioare
Să discutăm formula pentru aceste unghiuri în detaliu, după cum urmează:
Formula unghiului interior al poligoanelor
Unghiurile interioare ale unui poligon sunt cele formate între laturile sale adiacente și sunt egale în cazul unui poligon regulat. Numărul unghiurilor interioare corespunde numărului de laturi din poligon.
Suma unghiurilor interioare „S” dintr-un poligon cu „n” laturi se calculează ca
S = (n – 2) × 180°
Unde „n” reprezintă numărul de laturi.
Formula unghiului exterior al poligoanelor
Fiecare unghi exterior al unui poligon obișnuit este format prin extinderea uneia dintre laturile sale (fie în sensul acelor de ceasornic, fie în sens invers acelor de ceasornic) și măsurarea unghiului dintre această extensie și latura adiacentă. Într-un poligon regulat, toate unghiurile exterioare sunt egale
Suma totală a unghiurilor exterioare din orice poligon este fixată la 360°
Prin urmare,
Fiecare unghi exterior este dat de 360°/n
Unde „n” este numărul de laturi.
Suma unghiurilor interioare și exterioare corespunzătoare la orice vârf dintr-un poligon este întotdeauna de 180 de grade, exprimând o relație suplimentară:
Unghi interior + Unghi exterior = 180°
Unghi exterior = 180° – Unghi interior
Concluzie
- Poligonul este o figură închisă delimitată de trei sau mai multe segmente de linie
- Suma unghiurilor interioare: Suma tuturor unghiurilor interioare dintr-un poligon cu n laturi este dată de formula (n–2)×180°.
- Număr de diagonale: Pentru un poligon cu n laturi, numărul de diagonale este calculat folosind formula n(n–3)/2.
- Triunghiuri formate din diagonale: Numărul de triunghiuri formate prin unirea diagonalelor dintr-un singur colț al unui poligon este n–2.
- Unghiul interior al poligonului obișnuit: Măsura fiecărui unghi interior dintr-un poligon regulat cu n laturi este {(n–2)×180°}/n.
- Unghiul exterior al poligonului obișnuit: Măsura fiecărui unghi exterior dintr-un poligon regulat cu n laturi este de 360°/n.
De asemenea, Citeste
- Pătrat
- Paralelogram
- Dreptunghi
Exemple rezolvate pe poligon în matematică
Exemplul 1: Luați în considerare un patrulater cu patru laturi. Aflați suma tuturor unghiurilor sale interioare ale patrulaterului.
Soluţie:
Formula pentru suma unghiurilor interioare dintr-un poligon regulat cu n laturi = (n − 2) × 180°
Suma tuturor unghiurilor interioare ale patrulaterului = (4 – 2) × 180°
Suma tuturor unghiurilor interioare ale patrulaterului = 2 × 180°
Suma tuturor unghiurilor interioare ale patrulaterului = 360°
Prin urmare, suma tuturor unghiurilor interioare ale patrulaterului este de 360°.
Exemplul 2: Luați în considerare un poligon regulat cu un raport unghiular exterior și interior dat de 7:3. Determinați tipul de poligon.
Soluţie:
Raportul dintre unghiul exterior și interior este de 7:3.
Să presupunem că unghiul exterior și interior al unui poligon este 7x și 3x.
Suma unghiurilor exterioare și interioare ale oricărui poligon este de 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Unghi exterior = 18°
Număr de laturi = 360°/unghi exterior
= 360°/18°
= 20
Prin urmare, poligonul dat este un icosagon, deoarece are 20 de laturi.
Exemplul 3: Fiecare unghi exterior al unui poligon măsoară 90 de grade, determinați tipul de poligon?
Soluţie:
Conform formulei, fiecare unghi exterior = 360°/n
Aici n=număr laturi.
90°= 360°/n
n = 360°/90°= 4
Prin urmare, poligonul în cauză este un patrulater, deoarece are patru laturi.
Exemplul 4: Laturile sunt 10m, 10m, 8m, 8m, 5m, 5m, 9m, 9m. Câți metri de frânghie vor fi necesari pentru Perimetru?
Soluţie:
Pentru a găsi lungimea frânghiei necesară pentru perimetru, trebuie să însumăm lungimile tuturor laturilor:
Perimetrul = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Perimetrul = 64 m.
Prin urmare, va fi nevoie de un total de 64 de metri de frânghie pentru Perimetru.
Întrebări practice despre poligoane în geometrie
Mai jos sunt câteva întrebări practice bazate pe formula poligoanelor:
python sortând tupluri
Î1. Dat fiind că un unghi al unui pentagon este de 140°, determinați dimensiunea celui mai mare unghi dacă unghiurile rămase sunt în raportul 1:2:3:4.
Q2. Dacă suma unghiurilor interioare ale unui poligon este de 160°, găsiți numărul de laturi din poligon.
Q3. Numărul de laturi din două poligoane regulate este în raport de 2:3, iar raportul unghiurilor lor interioare este de 4:5. Găsiți numărul de laturi ale acestor poligoane.
Î4. Determinați suma totală a unghiurilor dintr-un heptagon.
Î5. Calculați suma unghiurilor exterioare dintr-un pentagon.
Î6. Câte laturi are un hexagon?
- 4
- 6
- 8
- 10
Î7. Care dintre următoarele nu este un poligon obișnuit?
- Triunghi
- Pătrat
- Pentagon
- Paralelogram
Întrebări frecvente despre poligoane în matematică
Ce este un poligon în matematică?
În matematică, un poligon se referă la o figură bidimensională închisă formată prin legătura a trei sau mai multe linii drepte. Termenul poligon este derivat din limba greacă, poli- semnifică mulți și gon reprezintă unghi.
Care este cel mai mic poligon?
Cel mai mic poligon format este un triunghi cu trei laturi.
Ce este 20-gon?
Un 20-gon este un poligon cu douăzeci de laturi în geometrie.
Care este suma totală a unghiurilor externe ale poligonului?
Suma unghiurilor exterioare ale unui poligon este 360°.
Poate un cerc să fie clasificat ca poligon?
Poligonul este o formă închisă alcătuită din segmente drepte. Cercul este o figură închisă, dar este făcut dintr-o curbă. Deci, un cerc nu este un poligon.
Care este suma unghiului interior al unui poligon?
Suma unghiului interior al unui poligon este dată de (n–2)×180° unde, n este numărul de laturi ale poligonului.
