Regresia logistică în programarea R este un algoritm de clasificare utilizat pentru a găsi probabilitatea succesului evenimentului și eșecului evenimentului. Regresia logistică este utilizată atunci când variabila dependentă este binară (0/1, adevărat/fals, da/nu). Funcția logit este utilizată ca funcție de legătură într-o distribuție binomială.
Probabilitatea unei variabile de rezultat binar poate fi prezisă folosind tehnica de modelare statistică cunoscută sub numele de regresie logistică. Este utilizat pe scară largă în multe industrii diferite, inclusiv marketing, finanțe, științe sociale și cercetare medicală.
Funcția logistică, denumită în mod obișnuit funcția sigmoidă, este ideea de bază care stă la baza regresiei logistice. Această funcție sigmoidă este utilizată în regresia logistică pentru a descrie corelația dintre variabilele predictoare și probabilitatea rezultatului binar.

Regresia logistică în programarea R
Regresia logistică este cunoscută și ca Regresia logistică binomială . Se bazează pe funcția sigmoidă în care ieșirea este probabilitate și intrarea poate fi de la -infinit la +infinit.
Teorie
Regresia logistică este cunoscută și ca model liniar generalizat. Deoarece este folosit ca tehnică de clasificare pentru a prezice un răspuns calitativ, valoarea lui y variază de la 0 la 1 și poate fi reprezentată prin următoarea ecuație:

Regresia logistică în programarea R
p este probabilitatea caracteristicii de interes. Raportul de șanse este definit ca probabilitatea de succes în comparație cu probabilitatea de eșec. Este o reprezentare cheie a coeficienților de regresie logistică și poate lua valori între 0 și infinit. Raportul de șanse de 1 este atunci când probabilitatea de succes este egală cu probabilitatea de eșec. Raportul de șanse de 2 este atunci când probabilitatea de succes este de două ori probabilitatea de eșec. Odds ratio de 0,5 este atunci când probabilitatea de eșec este de două ori probabilitatea de succes.
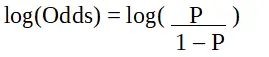
Regresia logistică în programarea R
Deoarece lucrăm cu o distribuție binomială (variabilă dependentă), trebuie să alegem o funcție de legătură care este cea mai potrivită pentru această distribuție.
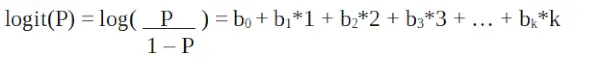
Regresia logistică în programarea R
Este un funcția logit . În ecuația de mai sus, paranteza este aleasă pentru a maximiza probabilitatea de a observa valorile eșantionului, mai degrabă decât pentru a minimiza suma erorilor pătrate (cum ar fi regresia obișnuită). Logit-ul este cunoscut și ca un jurnal de cote. Funcția logit trebuie să fie legată liniar de variabilele independente. Aceasta este din ecuația A, unde partea stângă este o combinație liniară a lui x. Aceasta este similară cu ipoteza MCO conform căreia y este legat liniar de x. Variabilele b0, b1, b2 … etc sunt necunoscute și trebuie estimate pe baza datelor de antrenament disponibile. Într-un model de regresie logistică, înmulțirea b1 cu o unitate schimbă logit-ul cu b0. Modificările P din cauza unei modificări de o unitate vor depinde de valoarea înmulțită. Dacă b1 este pozitiv, atunci P va crește și dacă b1 este negativ atunci P va scădea.
Setul de date
mtcars (testul de drum al automobilelor de tendință motor) cuprinde consumul de combustibil, performanța și 10 aspecte ale designului auto pentru 32 de automobile. Vine preinstalat cu dplyr pachet în R.
R
conține subșir de caractere java
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
șir în obiectul json
>
Efectuarea regresiei logistice pe un set de date
Regresia logistică este implementată în R folosind glm() prin antrenarea modelului folosind caracteristici sau variabile din setul de date.
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Împărțirea datelor
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Ieșire:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Interceptare) 1.58781 2.60087 0.610 0.5415 wt 1.36958 1.60524 0.853 0.3936 disp -0.02969 0.01577 -1.882 0.01577 -1.882 0.0. --- Signif. coduri: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Parametrul de dispersie pentru familia binomială considerată 1) Devianţă nulă: 34,617 pe 24 de grade de libertate Devianţă reziduală: 20,212 pe 22 de grade de libertate AIC: 26.212 Număr de iterații Fisher Scoring: 6>
- Apel: este afișat apelul de funcție utilizat pentru a se potrivi modelului de regresie logistică, împreună cu informații despre familie, formulă și date. Reziduuri de devianță: Acestea sunt reziduurile de devianță, care măsoară gradul de bunătate a modelului. Ele reprezintă discrepanțe între răspunsurile reale și probabilitatea prezisă de modelul de regresie logistică. Coeficienți: Acești coeficienți în regresia logistică reprezintă log odds sau logit ale variabilei de răspuns. Erorile standard legate de coeficienții estimați sunt prezentate în Std. Coloana Eroare. Coduri de semnificație: Nivelul de semnificație al fiecărei variabile de predicție este indicat de codurile de semnificație. Parametrul de dispersie: în regresia logistică, parametrul de dispersie servește ca parametru de scalare pentru distribuția binomială. Este setat la 1 în acest caz, indicând că dispersia presupusă este 1. Devianța nulă: Devianța nulă calculează abaterea modelului atunci când este luată în considerare doar interceptarea. Simbolizează abaterea care ar rezulta dintr-un model fără predictori. Deviația reziduală: Devianța reziduală calculează abaterea modelului după ce predictorii au fost ajustați. Reprezintă abaterea reziduală după luarea în considerare a predictorilor. AIC: Criteriul de informare Akaike (AIC), care ține cont de numărul de predictori, este un indicator al bunei potriviri a unui model. Penalizează modelele mai complicate pentru a preveni supraajustarea. Modelele care se potrivesc mai bine sunt indicate de valori mai mici ale AIC. Numărul de iterații de punctare Fisher: numărul de iterații necesare procedurii de punctare Fisher pentru a estima parametrii modelului este indicat de numărul de iterații.
Preziceți datele de testare pe baza modelului
R
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
java este instanceof
>
Ieșire:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Ieșire:
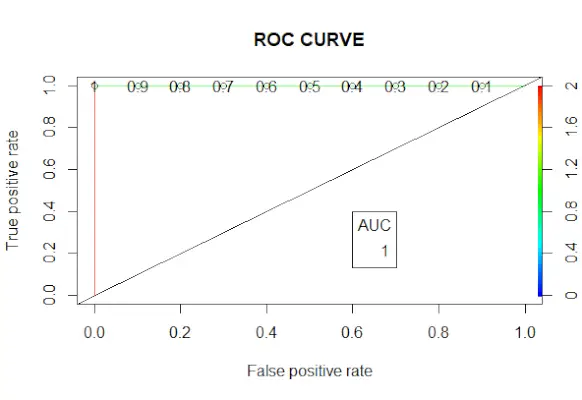
Curba ROC
Exemplul 2:
Putem efectua un model de regresie logistică setul de date Titanic în R.
R
converti boolean în șir
set c++
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Ieșire:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Interceptare) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.5+01e 01.-01e 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (Parametrul de dispersie pentru familia binomială considerată 1) Devianța nulă: 44.361 grade de libertate: 44.361 reziduală: 34.36 grade de libertate reziduale pe 26 de grade de libertate AIC: 56.361 Număr de iterații Fisher Scoring: 2>
Trasează curba ROC pentru setul de date Titanic
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
Ieșire:
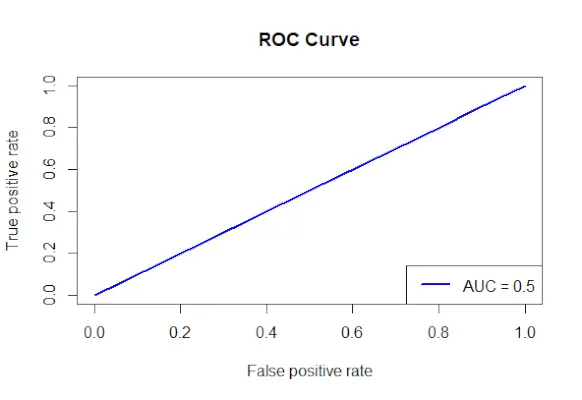
curba ROC
- Sunt specificați factorii utilizați pentru a prezice Supraviețuit, iar formula Clasa Supraviețuit + Sex + Vârstă este utilizată pentru a crea un model de regresie logistică.
- Folosind funcția predict(), predicțiile sunt făcute pe setul de date folosind modelul adaptat.
- Probabilitățile proiectate sunt combinate cu valorile reale ale rezultatului pentru a construi un obiect de predicție folosind metoda prediction() din pachetul ROCR.
- Măsura ratei pozitive adevărate (tpr) și măsurarea axei x a ratei pozitive false (fpr) sunt specificate, iar un obiect curbă ROC este creat folosind funcția performance() din pachetul ROCR.
- Obiectul curbă ROC (roc_obj), care specifică titlul principal, culoarea și lățimea liniei, este reprezentat folosind funcția plot().
- Utilizează funcția performance() cu măsură = auc pentru a determina valoarea AUC (zona sub curbă) și adaugă etichete și o legendă graficului.
