Arborele de căutare binar este o structură de date utilizată în informatică pentru organizarea și stocarea datelor într-o manieră sortată. Arborele de căutare binar urmează toate proprietățile arborelui binar și ale acestuia stânga copil conține valori mai mici decât nodul părinte și dreapta fiul conține valori mai mari decât nodul părinte. Această structură ierarhică permite eficiență In cautarea , Inserare , și Ștergere operațiuni asupra datelor stocate în arbore.

Arborele de căutare binar

Cuprins

• Ce este Arborele de căutare binar?
• Proprietățile arborelui de căutare binar
• Gestionarea valorilor duplicate în Arborele de căutare binar
• Operațiuni efectuate pe un BST
• 1. Căutarea unui nod în BST
• 2. Introduceți un nod într-un BST
• 3. Ștergeți un Nod al BST
• 4. Traversare (parcurgerea în ordine a BST)
• Aplicații ale BST
• Avantaje
• Dezavantaje
• Întrebări frecvente (întrebări frecvente) pe Arborele de căutare binar:

Ce este Arborele de căutare binar?

Arborele de căutare binar (BST) este un tip special de arbore binar în care copilul stâng al unui nod are o valoare mai mică decât valoarea nodului, iar copilul din dreapta are o valoare mai mare decât valoarea nodului. Această proprietate se numește proprietatea BST și face posibilă căutarea, inserarea și ștergerea eficientă a elementelor din arbore.

cast șir ca int java

Proprietățile arborelui de căutare binar:

• Subarborele din stânga al unui nod conține numai noduri cu chei mai mici decât cheia nodului.
• Subarborele din dreapta al unui nod conține numai noduri cu chei mai mari decât cheia nodului.
• Aceasta înseamnă că totul în stânga rădăcinii este mai mic decât valoarea rădăcinii și totul în dreapta rădăcinii este mai mare decât valoarea rădăcinii. Datorită acestei performanțe, o căutare binară este foarte ușoară.
• Subarborele din stânga și din dreapta trebuie să fie, de asemenea, un arbore de căutare binar.
• Nu trebuie să existe noduri duplicate (BST poate avea valori duplicate cu abordări diferite de manipulare)

Gestionarea valorilor duplicate în Arborele de căutare binar:

• Trebuie să urmăm un proces consecvent pe tot parcursul, adică fie să stocăm valoarea duplicată în stânga, fie să stocăm valoarea duplicată în partea dreaptă a rădăcinii, dar să fim consecvenți cu abordarea dvs.

Operații de bază pe arborele de căutare binar:

1. Căutarea unui nod în BST:

Căutarea în BST înseamnă a localiza un anumit nod în structura de date. În arborele de căutare binar, căutarea unui nod este ușoară datorită unei ordini specifice. Pașii căutării unui nod în arborele de căutare binar sunt enumerați după cum urmează -

1. Mai întâi, comparați elementul care trebuie căutat cu elementul rădăcină al arborelui.
   • Dacă rădăcina este potrivită cu elementul țintă, atunci returnați locația nodului.
   • Dacă nu se potrivește, atunci verificați dacă elementul este mai mic decât elementul rădăcină, dacă este mai mic decât elementul rădăcină, apoi treceți la subarborele din stânga.
   • Dacă este mai mare decât elementul rădăcină, atunci treceți la subarborele din dreapta.
2. Repetați procedura de mai sus în mod recursiv până când este găsită potrivirea.
3. Dacă elementul nu este găsit sau nu este prezent în arbore, atunci returnați NULL.

Acum, să înțelegem căutarea în arbore binar folosind un exemplu:

Mai jos este dat un BST și trebuie să căutăm elementul 6.

Cod:

Mai jos este implementarea căutării în BST:

// C++ function to search a given key in a given BST #include  using namespace std; struct node {  int key;  struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) {  struct node* temp  = new struct node;  temp->cheie = element;  temp->stânga = temp->dreapta = NULL;  temperatura de retur; } // O funcție utilitar pentru a insera // un nou nod cu cheia dată în BST struct node* insert(struct node* node, int key) { // Dacă arborele este gol, returnați un nou nod if (node ​​== NULL ) return newNode(cheie);  // În caz contrar, repetați în jos în arbore dacă (key< node->cheie) nod->left = insert(nod->left, key);  else if (key> node->key) node->right = insert(nod->right, key);  // Returnează nodul de returnare a indicatorului de nod (neschimbat); } // Funcție utilitar pentru a căuta o cheie într-un nod struct BST* search(struct node* root, int key) root->key == key) return root;  // Cheia este mai mare decât cheia root dacă (root->key< key)  return search(root->dreapta, cheie);  // Cheia este mai mică decât cheia rădăcină return search(root->stânga, cheie);>>>C 
// Java program to search a given key in a given BST class Node {  int key;  Node left, right;  public Node(int item) {  key = item;  left = right = null;  } } class BinarySearchTree {  Node root;  // Constructor  BinarySearchTree() {  root = null;  }  // A utility function to insert  // a new node with given key in BST  Node insert(Node node, int key) {  // If the tree is empty, return a new node  if (node == null) {  node = new Node(key);  return node;  }  // Otherwise, recur down the tree  if (key < node.key)  node.left = insert(node.left, key);  else if (key>node.key) node.right = insert(nod.right, key);  // Returnează nodul de returnare a indicatorului de nod (neschimbat);  } // Funcție utilitar pentru a căuta o cheie într-o căutare de nod BST (rădăcină de nod, cheie int) // Cazuri de bază: rădăcină este nulă sau cheia este prezentă la rădăcină dacă (rădăcină == nulă>
 Piton 
# Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Returnează (neschimbat) indicatorul de nod return node # Funcție utilitar pentru a căuta o cheie într-o căutare BST def (rădăcină, cheie): # Cazuri de bază: root este nul sau cheia este prezentă la rădăcină dacă rădăcină nu este None sau root.key == cheie: return root # Cheia este mai mare decât cheia rădăcină dacă root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
 JavaScript 
// Javascript function to search a given key in a given BST class Node { constructor(key) {  this.key = key;  this.left = null;  this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) {  return new Node(key); } // Otherwise, recur down the tree if (key < node.key) {  node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returnează nodul de returnare a indicatorului de nod (neschimbat); } // Funcție utilitar pentru a căuta o cheie într-o funcție BST search(root, key) { // Cazuri de bază: rădăcina este nulă sau cheia este prezentă la rădăcină dacă (rădăcină === null || root.key === cheie ) { returnează rădăcină; } // Cheia este mai mare decât cheia root dacă (root.key< key) {  return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
  
  
linspace numpy
 
    2.         Inserați un nod într-un BST         :     
O cheie nouă este întotdeauna introdusă la frunză. Începeți să căutați o cheie de la rădăcină până la un nod frunză. Odată ce este găsit un nod frunză, noul nod este adăugat ca un copil al nodului frunză.
 
  
 
    Cod:    
 
Mai jos este implementarea Inserării unui singur nod în Arborele de căutare binar:
C++ 
// Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp = (struct node*)malloc(  sizeof(struct node));  temp->cheie = element;  temp->stânga = temp->dreapta = NULL;  temperatura de retur; } // Funcție de inserare a unui nod nou cu // cheia dată în nodul struct BST* insert(nodul struct* nod, cheia int) { // Dacă arborele este gol, returnează un nod nou dacă (nodul == NULL) returnează newNode(cheie);  // În caz contrar, repetați în jos în arbore dacă (key< node->key) { nod->left = insert(node->left, key);  } else if (key> node->key) { nod->right = insert(nod->right, key);  } // Returnează nodul return pointer-ul nodului; }>>>Cnode.key) { node.right = insert(node.right, key);  } // Returnează nodul return nodul;  } }>>>Python3 
// Given Node Structure class Node {  constructor(key){  this.key = key;  this.left = null;  this.right = null;  } } // Function to insert a new node with // given key in BST function insert(node, key) {    // If the tree is empty, return a new node  if (node == null)  return new Node(key);  // Otherwise, recur down the tree  if (key < node.key)  {  node.left = insert(node.left, key);  }  else if (key>node.key) { node.right = insert(node.right, key);  } // Returnează nodul return pointer-ul nodului; }>>> 
    Complexitatea timpului:    O(N), unde N este numărul de noduri ale BST  
    Spațiu auxiliar:    O(1)
 
    3.          Ștergeți un nod al BST     :
Este folosit pentru a șterge un nod cu o cheie specifică din BST și a returna noul BST.
 
Diferite scenarii pentru ștergerea nodului:
 
    Nodul de șters este nodul frunză       :    
Este simplu, poți să-l anulezi.
  
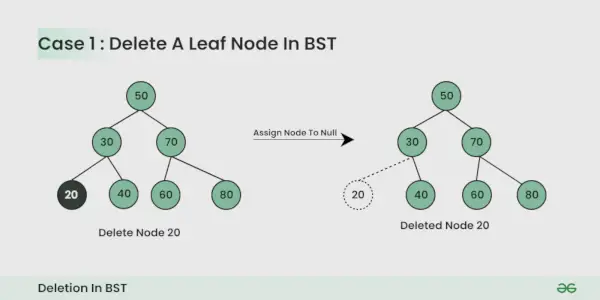
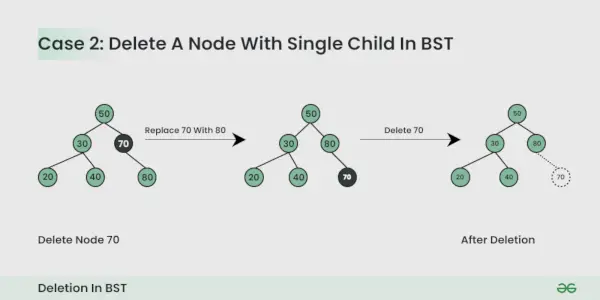
    Nodul de șters are un copil       :     
Puteți înlocui doar nodul cu nodul copil.
bou vs taur
  
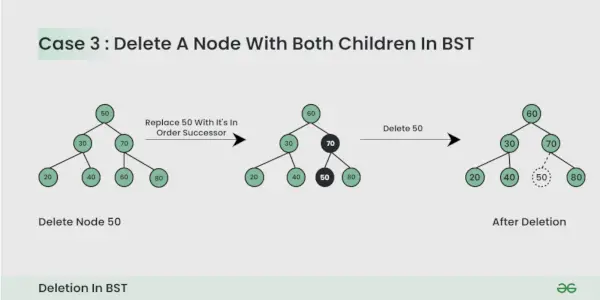
    Nodul de șters are doi copii       :     
Aici trebuie    ștergeți nodul este astfel încât arborele rezultat să urmeze proprietățile unui BST.    Trucul este să găsiți succesorul în ordine al nodului. Copiați conținutul succesorului în ordine în nod și ștergeți succesorul în ordine.
  
Aveți grijă de următoarele lucruri în timp ce ștergeți un nod al unui BST:
 
Trebuie să vă dați seama care va fi înlocuirea nodului care urmează să fie șters.
Doriți o întrerupere minimă a structurii arborelui existent
Poate lua nodul de înlocuire din subarborele din stânga sau din dreapta nodurilor șterse.
Dacă luăm if din subarborele din stânga, trebuie să luăm cea mai mare valoare din subarborele din stânga.
Dacă luăm if din subarborele din dreapta, trebuie să luăm cea mai mică valoare din subarborele din dreapta.
    Cod:    
 
Mai jos este implementarea ștergerii în BST:
C++cheie = element;  temp->stânga = temp->dreapta = NULL;  temperatura de retur; } // Funcție de inserare a unui nod nou cu // cheia dată în nodul struct BST* insert(nodul struct* nod, cheia int) { // Dacă arborele este gol, returnează un nod nou dacă (nodul == NULL) returnează newNode(cheie);  // În caz contrar, repetați în jos în arbore dacă (key< node->key) { nod->left = insert(node->left, key);  } else if (key> node->key) { nod->right = insert(nod->right, key);  } // Returnează nodul return pointer-ul nodului; } // Funcție care returnează nodul cu valoarea minimă // cheie găsită în acel arbore struct node* minValueNode(struct node* node) { struct node* current = node;  // Buclă în jos pentru a găsi frunza cea mai din stânga while (current && current->left != NULL) current = current->left;  curent de retur; } // Funcție care șterge cheia și // returnează noul struct node rădăcină* deleteNode(struct node* root, int key) { // caz de bază if (root == NULL) return root;  // Dacă cheia de șters este // mai mică decât cheia rădăcinii, // atunci se află în subarborele din stânga dacă (cheia< root->cheie) { root->left = deleteNode(root->stânga, cheie);  } // Dacă cheia de șters este // mai mare decât cheia rădăcinii, // atunci se află în subarborele din dreapta altfel if (key> root->key) { root->right = deleteNode(root-> dreapta, cheie);  } // Dacă cheia este aceeași cu cheia rădăcină, // atunci acesta este nodul // care trebuie șters altfel { // Nodul cu un singur copil // sau fără copil dacă (rădăcină->stânga == NULL) { struct node* temp = root->right;  liber(rădăcină);  temperatura de retur;  } else if (rădăcină->right == NULL) { struct node* temp = root->left;  liber(rădăcină);  temperatura de retur;  } // Nod cu doi copii: // Obține succesorul în ordine (cel mai mic // în subarborele din dreapta) struct node* temp = minValueNode(root->right);  // Copiați conținutul succesorului // în ordinea acestui nod root->key = temp->key;  // Sterge succesorul in ordine root->right = deleteNode(root->right, temp->key);  } returnează rădăcină; }>>>Javaroot.key) { root.right = deleteNode(root.right, key);  } // Dacă cheia este aceeași cu cheia rădăcină, // atunci acesta este nodul // care trebuie șters altfel { // Nodul cu un singur copil // sau fără copil dacă (root.left == null) { node temp = root.right;  temperatura de retur;  } else if (root.right == null) { node temp = root.left;  temperatura de retur;  } // Nod cu doi copii: // Obține succesorul în ordine (cel mai mic // în subarborele din dreapta) node temp = minValueNode(root.right);  // Copiați conținutul succesorului // în ordinea acestui nod root.key = temp.key;  // Sterge succesorul in ordine root.right = deleteNode(root.right, temp.key);  } returnează rădăcină;  }>>>Pitonroot.key: root.right = deleteNode(root.right, key) # Dacă cheia este aceeași cu cheia root, # atunci acesta este nodul # care trebuie șters altfel: # Nod cu un singur copil # sau niciun copil dacă root.left este None: temp = root.right root = None return temp elif root.right este None: temp = root.left root = None returnează temp # Nodul cu doi copii: # Obțineți succesorul în ordine (cel mai mic # din subarborele din dreapta) temp = minValueNode(root.right) # Copiați conținutul succesorului în ordine # în acest nod root.key = temp.key # Ștergeți succesorul în ordine root.right = deleteNode(root.right, temp.key) returnează rădăcină>> 
    4.         Traversare (parcurgere în ordine a BST)         :    
În cazul arborilor de căutare binari (BST), traversarea în ordine oferă noduri în ordine nedescrescătoare. Vizităm mai întâi copilul stâng, apoi rădăcina și apoi copilul drept.
 
Mai jos este implementarea modului de parcurgere în ordine a unui arbore de căutare binar:
C++cheie;  în ordine(rădăcină->dreapta);  } } // Cod driver int main() { /* Să creăm următorul BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // Crearea rădăcinii BST = insert(root, 50);  insert (rădăcină, 30);  insert (rădăcină, 20);  insert (rădăcină, 40);  insert (rădăcină, 70);  insert (rădăcină, 60);  insert (rădăcină, 80);  // Apel de funcție inorder(rădăcină);  întoarce 0; } // Acest cod este contribuit de shivanisinghss2110>>Ckey);  în ordine(rădăcină->dreapta);  } } // Cod driver int main() { /* Să creăm următorul BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // Crearea rădăcinii BST = insert(root, 50);  insert (rădăcină, 30);  insert (rădăcină, 20);  insert (rădăcină, 40);  insert (rădăcină, 70);  insert (rădăcină, 60);  insert (rădăcină, 80);  // Apel de funcție inorder(rădăcină);  întoarce 0; }>>>Java>Python3>>  
  Ieșire      Complexitatea timpului:    O(N), unde N este numărul de noduri ale BST  
    Spațiu auxiliar:    O(1)
Forța de curățare a memoriei cache npm
 
    Aplicații ale BST:    
    Algoritmi grafici:    BST-urile pot fi folosite pentru a implementa algoritmi de grafic, cum ar fi algoritmii de arbore de acoperire minim.
    Cozi prioritare:    BST-urile pot fi folosite pentru a implementa cozi de prioritate, unde elementul cu cea mai mare prioritate se află la rădăcina arborelui, iar elementele cu prioritate mai mică sunt stocate în subarbori.
    Arborele de căutare binar cu auto-echilibrare:    BST-urile pot fi utilizate ca structuri de date de auto-echilibrare, cum ar fi arborele AVL și arborele roșu-negru.
    Stocarea și preluarea datelor:    BST-urile pot fi folosite pentru a stoca și a prelua rapid date, cum ar fi bazele de date, unde căutarea unei anumite înregistrări se poate face în timp logaritmic.
    Avantaje:    
    Căutare rapidă:    Căutarea unei anumite valori într-un BST are o complexitate de timp medie de O(log n), unde n este numărul de noduri din arbore. Acest lucru este mult mai rapid decât căutarea unui element într-o matrice sau o listă legată, care au o complexitate de timp de O(n) în cel mai rău caz.
    Parcurs în ordine:    BST-urile pot fi parcurse în ordine, care vizitează subarborele din stânga, rădăcina și subarborele din dreapta. Aceasta poate fi folosită pentru a sorta un set de date.
    Spațiu eficient:    BST-urile sunt eficiente în spațiu, deoarece nu stochează nicio informație redundantă, spre deosebire de matrice și liste legate.
    Dezavantaje:    
    Copaci înclinați:    Dacă un arbore devine denaturat, complexitatea de timp a operațiilor de căutare, inserare și ștergere va fi O(n) în loc de O(log n), ceea ce poate face arborele ineficient.
    Timp suplimentar necesar:    Arborii de auto-echilibrare necesită timp suplimentar pentru a menține echilibrul în timpul operațiunilor de inserare și ștergere.
    Eficienţă:    BST-urile nu sunt eficiente pentru seturile de date cu multe duplicate, deoarece vor pierde spațiu.
Întrebări frecvente(Întrebări frecvente)pe arborele de căutare binar:
    1. Ce este un arbore binar de căutare?    
 
Un arbore de căutare binar (BST) este    un arbore binar în care fiecare nod din subarborele din stânga este mai mic decât rădăcina și fiecare nod din subarborele din dreapta are o valoare mai mare decât rădăcina    . Proprietățile unui arbore de căutare binar sunt recursive: dacă considerăm orice nod ca rădăcină, aceste proprietăți vor rămâne adevărate.
 
2. Ce este operațiunea arborelui de căutare binar?
 
Există trei operațiuni majore în Arborele de căutare binar:    1. Inserare, 2. Ștergere, 3. Căutare.    Datorită proprietăților sale, este eficient să căutați orice element în Arborele de căutare binar.
 
3. Ce este arborele de căutare binar și arborele AVL?
 
    Arborele de căutare binar       :    Un arbore de căutare binar (BST) este un arbore binar în care fiecare nod din subarborele din stânga este mai mic decât rădăcina, iar fiecare nod din subarborele din dreapta are o valoare mai mare decât rădăcina.
 
    Arborele AVL       :    Arborii binari de căutare (BST) care se auto-echilibrează și se rotesc automat sunt cunoscuți ca arbori AVL.
 
4. Care sunt utilizările Arborelui de căutare binar?
 
Arborii binari de căutare pot fi utilizați pentru a implementa tipuri de date abstracte, cum ar fi    seturi dinamice, tabele de căutare și cozi de prioritate,    și folosit în    algoritmi de sortare    cum ar fi sortarea copacilor.
 
5. Care este diferența dintre arborele binar de căutare și arborele binar?
 
Un arbore binar de căutare este un arbore care urmează o anumită ordine pentru a aranja elementele, în timp ce arborele binar nu urmează nicio ordine.
 
    Articole similare:    
 
     Aplicarea BST     
     Aplicații, avantaje și dezavantaje ale arborelui de căutare binar     
     Inserarea în arborele binar de căutare (BST)     
     Căutarea în arborele binar de căutare (BST)     
     Ștergerea în arborele binar de căutare (BST)