Zerurile unui polinom sunt acele valori reale, imaginare sau complexe atunci când sunt introduse în polinom în loc de o variabilă, rezultatul devine zero (după cum sugerează și numele zero). Polinoamele sunt folosite pentru a modela unele fenomene fizice care se întâmplă în viața reală, ele sunt foarte utile în descrierea situațiilor matematic.

Zerourile unui polinom sunt toate valorile x care fac polinomul egal cu zero. Zerourile unui polinom ne spun despre intersecția cu x ale graficului polinomului. În acest articol, vom discuta despre zerourile unui polinom, cum să le găsiți, teorema factorului etc.

Cuprins

• Ce sunt zerourile de polinoame?
• Zerourile formulei polinomiale
• Cum să găsiți zero al unui polinom?
• Pentru polinom liniar
• Pentru polinom pătratic
• Pentru polinom cubic
• Teorema factorului
• Relația dintre zerouri și coeficient
• Relația dintre zerouri și coeficient pentru ecuația cuadratică
• Relația dintre zerouri și coeficient pentru ecuația cubică
• Formarea ecuației cu zerourile polinomului
• Zerouri în graficul polinoamelor
• Teorema fundamentală a algebrei liniare
• Multiplicitatea unei rădăcini
• Articole legate de Zeros of Polynomial
• Exemple de probleme pe zerourile polinomului
• Practicați probleme pe zerourile polinomului

Ce sunt zerourile de polinoame?

Pentru un polinom P(x), spunem că x = a este zero al polinomului dacă P(a) = 0, iar toate astfel de zerouri ale unui polinom sunt denumite în mod obișnuit zerouri ale unui polinom. De exemplu, luați în considerare f(x) = 3x – 12. Acum, puneți x = 4 în polinom, adică f(4) = 3×4 – 12 = 0. Astfel, x = 4 este un zero al polinomului f( x) = 3x – 12.

Exemplu: Pentru f(x) = x ³ – 6x ² + 11x – 6, x = 1 este zero?

Soluţie:

Pentru a verifica dacă x = 1 este zero pentru f(x) = x³– 6x²+ 11x – 6 sau nu, pune x = 1 în (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Astfel, x = 1 este un zero al lui f(x).

Zerourile formulei polinomiale

Pentru un polinom liniar de forma ax + b, zeroul său este dat de x = -b/a.

Pentru un polinom pătratic de forma ax²+ bx + c, zero este dat de x = {- b ± √D}/2a unde D este discriminant dat de b²– 4ac.

Cum să găsiți zero al unui polinom?

Putem găsi zerourile polinomului pentru diferite tipuri de polinoame folosind diferite metode care sunt discutate mai jos.

• Pentru polinom liniar
• Pentru polinom pătratic
• Pentru polinom cubic

Pentru polinom liniar

Pentru polinoamele liniare, găsirea zero este cea mai ușoară dintre toate. deoarece există un singur zero și care poate fi calculat și prin simpla rearanjare a polinomului după polinomul echivalent cu 0.

De exemplu, găsiți zero pentru polinomul liniar f(x) = 2x – 7.

Soluţie:

Pentru a găsi zero pentru f(x), egalați f(x) cu 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Pentru polinom pătratic

Există diferite metode pentru a găsi rădăcinile sau zerourile unui polinom pătratic, cum ar fi împărțirea termenului de mijloc, o formulă pătratică cunoscută și sub numele de formula Shree Dharacharya și completarea pătratului care este oarecum similar cu formula pătratică, deoarece vine formula pătratică. din completarea pătratului pentru ecuația generală pătratică.

Află mai multe despre rezolvarea ecuațiilor pătratice sau polinoame și cum să le rezolve. Următoarele exemple arată în detaliu metoda de găsire a zerourilor polinoamelor pătratice.

Exemplul 1: Aflați zerourile pentru P(x) = x ² + 2x – 15.

Răspuns:

X²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Exemplul 2: Aflați zerourile pentru P(x) = x ² – 16x + 64.

Răspuns:

X²– 16x + 64 = 0

Comparând cu toporul²+ bx + c = 0,

obținem, a = 1, b = -16 și c = 64.

Prin urmare,

⇒ x = 8, 8

Pentru polinom cubic

Pentru a găsi zerouri de cubic există multe moduri, cum ar fi teorema rădăcinii raționale și diviziunea lungă împreună. O metodă de găsire a rădăcinilor polinomului cubic sau a oricărui polinom de grad superior este următoarea:

Pasul 1: Utilizați teorema rădăcinii raționale pentru a găsi rădăcinile posibile. adică, dacă un polinom are o rădăcină rațională, aceasta trebuie să fie împărțirea lui p/q, unde p este constanta întreagă și q este coeficientul principal.

Pasul 2: După ce ați găsit o rădăcină, împărțiți polinomul cu factorul format de acea rădăcină folosind diviziunea lungă și scrieți polinomul ca produs al coeficientului și al dividendului.

Pasul 3: Dacă câtul este o expresie pătratică, rezolvați-l prin metodele menționate mai sus pentru polinoamele pătratice. Dacă nu este un polinom de gradul 2, repetați pașii 1 și 2 până când coeficientul devine un polinom cu gradul 2.

Pasul 4: Rezultatul pasului 3 este factorii necesari, iar echivalând factorul cu 0, putem găsi zerourile polinomului.

Exemplu: Aflați zerourile polinomului cubic p(x) = x ³ + 2x ² – 5x – 6.

Soluţie:

p(x) = x³+ 2x²– 5x – 6

Ca p/q = -6

Prin teorema rădăcinii raționale, toate rădăcinile raționale posibile ale polunomului sunt divizori ai p/q.

Astfel, divizori = ±1, ±2, ±3, ±6

x = -1, în p(x), obținem

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Astfel, prin teorema factorilor, x + 1 este factorul lui p(x).

Astfel, x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Pentru zerouri, p(x) = 0,

Zerourile lui p(x) sunt x = -1, x = 2 și x = -3.

Teorema factorului

Pentru polinomul P(x), teorema factorului afirmă că dacă x =a este zero al lui P(X) dacă x – a este un factor al lui P(x). adică ambele condiții următoare ar trebui să fie adevărate.

• Dacă a este zero al lui P(x), atunci x−a va fi un factor al lui P(x)
• Dacă x−a este un factor al lui P(x), atunci a va fi un zero al lui P(x)

Acest lucru poate fi verificat analizând exemplele anterioare. Teorema factorilor poate duce la unele rezultate interesante, care sunt următoarele:

Rezultatul 1: Dacă P(x) este un polinom de gradul n și r este un zero al lui P(x), atunci P(x) poate fi scris în următoarea formă:

P(x) = (x – r) Q(x)

Unde Q(x) este un polinom de grad n-1 și poate fi aflat prin împărțirea P(x) cu (x – r).

Rezultatul 2: Dacă P(x) = (x-r)Q(x) și x = t este un zero al lui Q(x), atunci x = t va fi, de asemenea, un zero al lui P(x).

Pentru a verifica faptul de mai sus,

Să presupunem că t este zero Q(x), ceea ce înseamnă Q(t) = 0.

Știm că r este un zero al polinomului P(x), unde P(x) = (x – r) Q(x),

Deci trebuie să verificăm dacă x = t este și un zero al lui P(x), să punem x = t în P(x)

⇒ P(t) = (t – r) Q(t) = 0

Deci, x = t este, de asemenea, un zero P(x).

Prin urmare, Proved.

Relația dintre zerouri și coeficient

Relația dintre zerouri și coeficientul ecuației pătratice și cubice este discutată mai jos.

Relația dintre zerouri și coeficient pentru ecuația cuadratică

Pentru o ecuație pătratică de forma ax²+ bx + c = 0, dacă cele două zerouri ale ecuației pătratice sunt α și β, atunci

• Suma rădăcinii = α + β = -b/a
• Produsul rădăcinilor = α × β = c/a

Relația dintre zerouri și coeficient pentru ecuația cubică

Dacă α, β și γ sunt rădăcina polinomului cubic ax³+ bx²+ cx + d = 0, atunci relația dintre zerourile și coeficienții săi este dată după cum urmează:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Formarea ecuației cu zerourile polinomului

• Pentru un polinom pătratic cu zerouri α și β, polinomul pătratic este dat de

X ² – (a + b)x + ab .

• Pentru un polinom cubic cu trei zerouri α, β și γ, polinomul cubic este dat de

X ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Zerouri în graficul polinoamelor

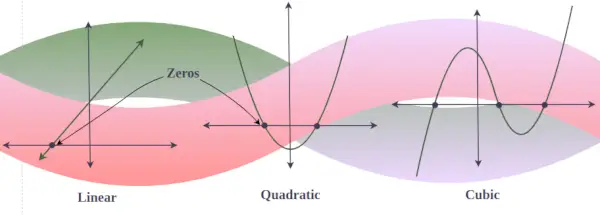
În graficul oricărui polinom y = f(x), zerourile reale sunt punctul pentru care graficul se intersectează sau atinge axa x. (deoarece un grafic cu un zero imaginar nu taie niciodată axa x). Cu alte cuvinte, dacă există 3 soluții reale ale unui polinom cub, atunci graficul acelui polinom cub intersectează axa x de trei ori, dar dacă există o singură soluție reală pentru un polinom cub, atunci graficul taie doar axa x. o singura data.

Teorema fundamentală a algebrei liniare

Dacă P(x) este un polinom de grad n, atunci P(x) va avea exact n zerouri, dintre care unele se pot repeta.

Aceasta înseamnă că dacă listăm toate zerourile și listăm fiecare de k ori când k este multiplicitatea sa. Vom avea exact n numere în listă. Acest lucru poate fi util, deoarece ne poate da o idee despre câte zerouri ar trebui să fie acolo într-un polinom. Deci, putem înceta să căutăm zerouri odată ce atingem numărul necesar de zerouri.

ce este modulo în c++

Multiplicitatea unei rădăcini

Să presupunem că avem un polinom P(x) = 0 care se factorizează în,

P(x) = (x – r) ^k (x – a) ^m

Dacă r este zero al unui polinom și exponentul pe termenul său care a produs rădăcina este k, atunci spunem că r are multiplicitatea k . Deseori se numesc zerouri cu o multiplicitate de 1 simplu zerourile și zerourile cu o multiplicitate de 2 se numesc rădăcini duble ale polinomului.

Exemplu: P(x) este un polinom de gradul 5, care a fost factorizat pentru dvs. Enumerați rădăcinile și multiplicitatea lor.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

Soluţie:

Dat, P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Pentru a găsi zerouri, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Observați că -1 apare de două ori ca zero, deci multiplicitatea lui este 2, în timp ce multiplicitatea lui zero 2 este 3.

Articole legate de Zeros of Polynomial

• Polinom
• Rădăcinile ecuației cuadratice
• Expresie algebrica

Exemple de probleme pe zerourile polinomului

Problema 1: Având în vedere că x = 2 este un zero al lui P(x) = x ³ +2x ² −5x−6. Găsiți celelalte două zerouri.

Soluţie:

Din teorema fundamentală pe care am studiat-o mai devreme, putem spune că P(x) va avea 3 zerouri deoarece este un polinom de trei grade. Una dintre ele este x = 2.

Deci putem rescrie P(x),

P(x) = (x – 2) Q(x)

Pentru a găsi celelalte două zerouri, trebuie să aflăm Q(x).

Q(x) poate fi găsit prin împărțirea P(x) la (x-2).

După împărțire, Q(x) iese a fi,

Q(x) = x²+ 4x + 3

Cele două zerouri rămase pot fi găsite din aceasta,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Astfel, celelalte două zerouri sunt x = -1 și x = -3.

Problema 2: Având în vedere că x = r este un zero al unui polinom, aflați celelalte zerouri ale polinomului.

P(x) = x ³ -6x ² −16x; r = −2

Soluţie:

Știm că x = -2 este zero,

Deci, P(x) poate fi rescris ca, P(x) = (x + 2) Q(x) {Prin utilizarea algoritmului de divizare}

Acum, pentru a găsi Q(x), facem același lucru ca și în întrebarea anterioară, împărțim P(x) cu (x + 2).

Primim,

Q(x) = x²– 8x

Acum, pentru a găsi celelalte două zerouri, factorizați Q(x)

Q(x) = x (x – 8) = 0

Deci, zerourile sunt x = 0, 8.

Astfel, avem trei zerouri, x = -2, 0, 8.

Problema 3: Aflați zerourile polinomului, 4x ³ -3x ² -25x-6 = 0

Soluţie:

Truc pentru a rezolva ecuații polinomiale cu gradul 3,

Găsiți cel mai mic număr întreg care poate face valoarea polinomului 0, începeți cu 1,-1,2 și așa mai departe...

constatăm că pentru x = -2 obținem valoarea expresiei să fie zero.

Prin urmare, una dintre rădăcini este -2.

Conform teoremei factorilor, dacă a este unul dintre zerourile polinomului, deci (x-a) este factorul polinomului dat.

Astfel, în urma acestui {x – (-2)} = (x+2) este un factor pof deasupra polinomului.

Obținem o ecuație pătratică și un zero este deja acolo.

(4x²-11x-3)(x+2) = 0

Factorizați ecuația pătratică,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Problema 4: Aflați zerourile polinomului, 4x ⁶ – 16x ⁴ = 0

Soluţie:

Polinomul are până la gradul 6, prin urmare, există 6 zerouri ale polinomului.

4x⁴(X²-4) = 0

4x⁴(X²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Prin urmare, x= 0, 0, 0, 0, 2, -2

Problema 5: Aflați zerourile funcției polinomiale f(x) = x ³ – 2x ² – 5x + 6

Soluţie:

Pentru a găsi zerourile acestui polinom, punem f(x) = 0 și rezolvăm pentru x:

f(x) = x³– 2x²– 5x + 6 = 0

Ca d/a = 6

Prin teorema rădăcinii raționale, toate rădăcinile raționale posibile ale polunomului sunt:

Divizori ai d/a = ±1, ±2, ±3, ±6

x = 1, în p(x), obținem

f(1) = (1)³– 2(1)²– 5 alineatul (1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Astfel, prin teorema factorilor, x – 1 este factorul lui p(x).

Astfel, x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

X³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Pentru zerouri, p(x) = 0,

Zerourile lui p(x) sunt x = 1, x = -2 și x = 3.

Practicați probleme pe zerourile polinomului

1. Aflați toate zerourile polinomului f(x) = x ³ – 6x ² + 11x – 6

2. Să se determine toate zerourile polinomului g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Aflați zerourile polinomului h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Să se determine toate zerourile polinomului p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Întrebări frecvente despre zerourile polinomului

Ce sunt zerourile unui polinom?

Aceste astfel de valori reale, pentru valoarea polinomului devine 0, adică dacă p(x) este un polinom și p(a) = 0, atunci x = a este zero al lui p(x).

Cum să găsiți zerourile unui polinom?

Există diferite metode pentru diferite polinoame pentru a găsi zerouri, cum ar fi pentru revărsarea termenului de mijloc și formula pătratică. Pentru rearanjarea liniară, simplă a variabilelor și pentru cubic folosim o combinație de teorema rădăcinii raționale, diviziunea lungă, teorema factorilor și teorema restului.

Poate un polinom să aibă mai mult de un zero?

Da, un polinom poate avea mai mult de un zero, de fapt, polinomul de n grade poate avea cel mult n zerouri reale.

Care este multiplicitatea unui zero al unui polinom?

În procesul de factorizare, un factor sau un zero al unui polinom, apoi de mai multe ori a apărut un factor sau un zero, adică multiplicitatea acelei rădăcini.

python __dict__

Care este teorema fundamentală a algebrei?

Teorema fundamentală a stărilor algebrei Dacă P(x) este un polinom de grad n, atunci P(x) va avea exact n zerouri, dintre care unele se pot repeta.

Un polinom cu grad n are întotdeauna n rădăcini reale?

Nu, un polinom cu gradul n nu are întotdeauna n rădăcini reale, deoarece unele rădăcini pot fi numere imaginare sau complexe.

Care este gradul polinomului zero?

Gradul polinomului zero este zero.