Termenul Memorarea provine din cuvântul latin memorandum ( a ține minte ), care este în mod obișnuit prescurtat în memo în engleza americană și care înseamnă a transforma rezultatele unei funcții în ceva de reținut.
În calcul, memorarea este folosită pentru a accelera programele de calculator prin eliminarea calculului repetitiv al rezultatelor și prin evitarea apelurilor repetate la funcții care procesează aceeași intrare.

Ce este memorarea
Cuprins
- Ce este memorarea?
- De ce se folosește Memoization>
- Unde să folosiți Memoization?
- Tipuri de memorare
- Cum este folosită tehnica de memorare în programarea dinamică?
- Cum este diferită memorarea de tabulare?
- Probleme practice de codificare pentru memorare
- Întrebări frecvente
- 1) Este memorarea mai bună decât DP?
- 2) Memorarea este aceeași cu stocarea în cache?
- 3) De ce memorarea este de sus în jos?
- 4) Memorizarea folosește recursiunea?
- 5) Ar trebui să folosesc tabularea sau memorarea?
- 6) Unde se folosește memorizarea?
- 7) De ce se numește memorare?
- 8) Cum reduce complexitatea timpului memorizarea?
- 9) Care este diferența dintre memorare și stocare în cache?
- 10) De ce tabularea este mai rapidă decât memorarea?
- Concluzie
De ce se folosește Memoization?
Memorizarea este o formă specifică de stocarea în cache care este folosit în programare dinamică . Scopul memorării în cache este de a îmbunătăți performanța programelor noastre și de a menține datele accesibile care pot fi utilizate ulterior. Practic stochează rezultatul calculat anterior al subproblemei și folosește rezultatul stocat pentru aceeași subproblemă. Acest lucru elimină efortul suplimentar de a calcula din nou și din nou pentru aceeași problemă. Și știm deja că, dacă aceeași problemă apare din nou și din nou, atunci acea problemă este recursivă în natură.
Unde să folosiți Memoization?
Putem folosi tehnica de memorare în cazul în care utilizarea rezultatelor calculate anterior intră în imagine. Acest tip de problemă este utilizat în principal în contextul recursiunea , mai ales cu probleme care implică subprobleme suprapuse .
Să luăm un exemplu în care aceeași subproblemă se repetă din nou și din nou.
Exemplu pentru a arăta unde să utilizați memorarea:
Let us try to find the factorial of a number .>
Mai jos este a metoda recursivă pentru a găsi factorialul unui număr:
int factorial (unsigned int n)
{
dacă (n == 0)
întoarcere 1;
return n * factorial(n – 1);
}
Ce se întâmplă dacă folosim această metodă recursivă?
Dacă scrieți codul complet pentru fragmentul de mai sus, veți observa că vor exista 2 metode în cod:
1. factorial(n) 2. main()>
Acum, dacă avem mai multe interogări pentru a găsi factorialul, cum ar fi găsirea factorialului de 2, 3, 9 și 5, atunci va trebui să apelăm metoda factorial() de 4 ori:
factorial(2) factorial(3) factorial(9) factorial(5)>
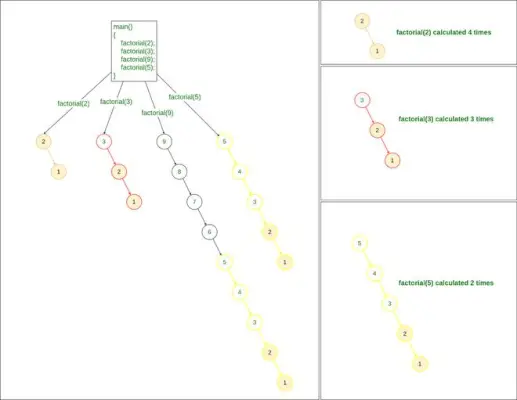
Metoda recursiva pentru a gasi factorial
Deci, este sigur să spunem că pentru a găsi factoriale de numere K numere, complexitatea de timp necesară va fi O(N*K)
- PE) pentru a găsi factorialul unui anumit număr și
- SĂGEATĂ) pentru a apela metoda factorial() K ori diferite.
Cum poate ajuta Memoization cu astfel de probleme?
Dacă observăm în problema de mai sus, în timp ce calculăm factorial de 9:
etichete html
- Calculăm factorialul de 2
- De asemenea, calculăm factorialul de 3,
- și calculăm și factorul de 5
Prin urmare, dacă stocăm rezultatul fiecărui factorial individual la prima dată de calcul, putem returna cu ușurință factorialul oricărui număr necesar în doar O(1) timp. Acest proces este cunoscut ca Memorarea .
Soluție folosind memorarea (Cum funcționează memorarea?):
Dacă găsim mai întâi factorialul lui 9 și stocăm rezultatele subproblemelor individuale, putem tipări cu ușurință factorialul fiecărei intrări în O(1).
Prin urmare, complexitatea de timp pentru a găsi numere factoriale folosind memorarea va fi PE)
- PE) pentru a găsi factorialul celui mai mare input
- O(1) pentru a imprima factorialul fiecărei intrări.
Tipuri de memorare
Implementarea memorizării depinde de parametrii în schimbare care sunt responsabili pentru rezolvarea problemei. Există diferite dimensiuni ale stocării în cache care sunt utilizate în tehnica de memorare, mai jos sunt câteva dintre ele:
- Memorare 1D: Funcția recursivă care are un singur argument a cărui valoare nu a fost constantă după fiecare apel de funcție.
- Memorare 2D: Funcția recursivă care are doar două argumente a căror valoare nu a fost constantă după fiecare apel de funcție.
- Memorizare 3D : Funcția recursivă care are doar trei argumente ale căror valori nu au fost constante după fiecare apel de funcție.
Cum este utilizată tehnica de memorare în programarea dinamică?
Programarea dinamică ajută la rezolvarea eficientă a problemelor care au subprobleme suprapuse și proprietăți optime ale substructurii. Ideea din spatele programării dinamice este de a împărți problema în sub-probleme mai mici și de a salva rezultatul pentru utilizare ulterioară, eliminând astfel nevoia de a calcula rezultatul în mod repetat.
Există două abordări pentru a formula o soluție de programare dinamică:
- Abordare de sus în jos: Această abordare urmează memorare tehnică . Se compune din recursiunea și stocarea în cache . În calcul, recursiunea reprezintă procesul de apelare în mod repetat a funcțiilor, în timp ce memoria cache se referă la procesul de stocare a rezultatelor intermediare.
- Abordarea de jos în sus: Această abordare folosește intabulare tehnică pentru a implementa soluția de programare dinamică. Se adresează aceleași probleme ca înainte, dar fără recursivitate. În această abordare, iterația înlocuiește recursiunea. Prin urmare, nu există nicio eroare de depășire a stivei sau supraîncărcarea procedurilor recursive.
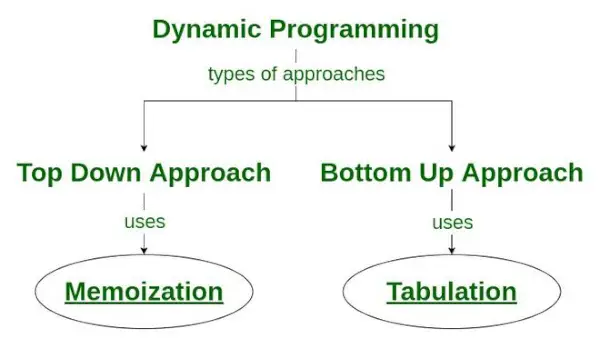
Cum este utilizată tehnica de memorare în programarea dinamică
Cum este diferită memorarea de tabulare?

Tabulare vs memorare
Pentru mai multe detalii vă rugăm să consultați: Tabulare vs. memorare
Probleme practice de codificare privind memorarea
| Întrebare | Articol | Practică | Video |
|---|---|---|---|
| Numărați modalitățile de a ajunge la a noua scară | Vedere | Rezolva | Ceas |
| Problemă cu spargerea cuvintelor | DP-32 | Vedere | Rezolva | Ceas |
| Program pentru numerele Fibonacci | Vedere | Rezolva | Ceas |
| al n-lea număr catalan | Vedere | Rezolva | Ceas |
| Problema Minei de Aur | Vedere | Rezolva | Ceas |
| Problema sumei subsetului | Vedere | Rezolva | Ceas |
| Tăierea unei tije | Vedere | Rezolva | Ceas |
| Calea costului minim | Vedere | Rezolva | Ceas |
| Numărul minim de sărituri pentru a ajunge la capăt | Vedere | Rezolva | Ceas |
| Cel mai lung subșir palindromic | Setul 1 | Vedere | Rezolva | Ceas |
| Cea mai lungă secvență care se repetă | Vedere | Rezolva | Ceas |
| Numărați modalitățile de a ajunge la a n-a treaptă folosind pasul 1, 2 sau 3 | Vedere | Rezolva | Ceas |
| Numărați moduri diferite de a exprima N ca sumă a 1, 3 și 4 | Vedere | Rezolva | Ceas |
| Numărați numărul de moduri de a parcurge o distanță | Vedere | Rezolva | Ceas |
| Numărul de tablouri cu elemente consecutive cu valori diferite | Vedere | Rezolva | Ceas |
| Cea mai mare sumă Subbarray contiguă | Vedere | Rezolva | Ceas |
| Cea mai mică sumă subbary contiguă | Vedere | Rezolva | Ceas |
| Căi unice într-o grilă cu obstacole | Vedere | Rezolva | Ceas |
| Diferite moduri de a suma n folosind numere mai mari sau egale cu m | Vedere | Rezolva | Ceas matrice de sortare în java |
Întrebări frecvente (FAQs) despre Memoization
1: Este memorarea mai bună decât DP?
Memorizarea este abordarea de sus în jos pentru rezolvarea unei probleme cu programarea dinamică. Se numește memorare deoarece vom crea un memoriu pentru valorile returnate din rezolvarea fiecărei probleme.
2: Memorarea este aceeași cu stocarea în cache?
Memorarea este de fapt un tip specific de stocare în cache. Termenul de stocare în cache se poate referi în general la orice tehnică de stocare (cum ar fi cachingul HTTP) pentru utilizare ulterioară, dar memorarea se referă mai precis la funcția de stocare în cache care returnează valoarea.
3: De ce memorarea este de sus în jos?
Abordarea de sus în jos descompune problema mare în mai multe subprobleme. dacă subproblema este deja rezolvată, reutilizați răspunsul. În caz contrar, Rezolvați subproblema și stocați rezultatul într-o memorie.
4: Memorizarea folosește recursiunea?
Memorarea urmează abordarea de sus în jos pentru rezolvarea problemei. Constă în recursivitate și stocare în cache. În calcul, recursiunea reprezintă procesul de apelare în mod repetat a funcțiilor, în timp ce memoria cache se referă la procesul de stocare a rezultatelor intermediare.
5: Ar trebui să folosesc tabularea sau memorarea?
Pentru problemele care necesită rezolvarea tuturor subproblemelor, tabularea depășește de obicei memorarea cu un factor constant. Acest lucru se datorează faptului că tabularea nu are o suprasarcină a recursiunii, ceea ce reduce timpul de rezolvare a stivei de apeluri recursive din memoria stivei.
Ori de câte ori trebuie rezolvată o subproblemă pentru ca problema inițială să fie rezolvată, memorarea este de preferat, deoarece o subproblemă este rezolvată leneș, adică doar calculele necesare sunt efectuate.
6: Unde se folosește memorarea?
Memorizarea este o tehnică de optimizare folosită pentru a accelera programele de calculator prin memorarea în cache a rezultatelor apelurilor de funcții costisitoare și returnându-le atunci când aceleași intrări sunt întâlnite din nou.
7: De ce se numește memorare?
Termenul de memorare provine din cuvântul latin memorandum (a aminti), care este de obicei prescurtat la memo în engleza americană și care înseamnă a transforma rezultatele unei funcții în ceva de reținut.
8: Cum reduce complexitatea timpului memorarea?
Rezolvarea aceleiași probleme din nou și din nou necesită timp și crește complexitatea de rulare a programului general. Această problemă poate fi rezolvată prin menținerea unui cache sau memorie în care vom stoca rezultatul deja calculat al problemei pentru o anumită intrare. Astfel încât, dacă nu dorim să recalculăm aceeași problemă, putem pur și simplu să folosim rezultatul care este stocat în memorie și să reducem complexitatea timpului.
9: Care este diferența dintre memorare și stocare în cache?
Memorizarea este de fapt un tip specific de stocare în cache care implică stocarea în cache a valorii returnate a unei funcții pe baza intrării. Memorarea în cache este un termen mai general. De exemplu, stocarea în cache HTTP este stocarea în cache, dar nu este memorare.
10: De ce tabularea este mai rapidă decât memorarea?
Tabularea este de obicei mai rapidă decât memorarea, deoarece este iterativă și rezolvarea subproblemelor nu necesită suprasolicitare a apelurilor recursive.
Memorizarea este o tehnică utilizată în informatică pentru a accelera execuția funcțiilor recursive sau costisitoare din punct de vedere computațional prin memorarea în cache a rezultatelor apelurilor de funcții și returnarea rezultatelor stocate în cache atunci când aceleași intrări apar din nou.
Ideea de bază a memorării este de a stoca rezultatul unei funcții pentru un set dat de intrări și de a returna rezultatul stocat în cache dacă funcția este apelată din nou cu aceleași intrări. Această tehnică poate economisi timp de calcul, în special pentru funcțiile care sunt apelate frecvent sau au o complexitate mare în timp.
Iată un ghid pas cu pas pentru implementarea memorării:
Identificați funcția pe care doriți să o optimizați folosind memorarea. Această funcție ar trebui să aibă calcule repetate și costisitoare pentru aceeași intrare.
Creați un obiect dicționar pentru a stoca rezultatele din cache ale funcției. Cheile dicționarului ar trebui să fie parametrii de intrare ai funcției, iar valorile ar trebui să fie rezultatele calculate.
La începutul funcției, verificați dacă parametrii de intrare sunt deja prezenți în dicționarul cache. Dacă sunt, returnați rezultatul stocat în cache.
Dacă parametrii de intrare nu sunt în dicționarul cache, calculați rezultatul și stocați-l în dicționarul cache cu parametrii de intrare ca cheie.
Returnează rezultatul calculat.
Iată un exemplu de cod Python de implementare a memorizării folosind un dicționar:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Ieșire
>
În codul de mai sus, definim o funcție numită Fibonacci care calculează al n-lea număr din șirul Fibonacci. Folosim un obiect dicționar numit cache pentru a stoca rezultatele apelurilor de funcții. Dacă parametrul de intrare n este deja prezent în dicționarul cache, returnăm rezultatul stocat în cache. În caz contrar, calculăm rezultatul folosind apeluri recursive la funcția Fibonacci și îl stocăm în dicționarul cache înainte de a-l returna.
Memorizarea poate fi folosită pentru a optimiza performanța multor funcții care au calcule repetate și costisitoare. Prin memorarea în cache a rezultatelor apelurilor de funcții, putem evita calculele inutile și putem accelera execuția funcției.
Concluzie
Memorizarea este un concept de programare și poate fi aplicat oricărui limbaj de programare. Scopul său absolut este de a optimiza programul. De obicei, această problemă este observată atunci când programele efectuează calcule grele. Această tehnică memorează în cache tot rezultatul anterior care este calculat, astfel încât să nu fie nevoie să recalculeze pentru aceeași problemă.
Articole similare:
- Memorare folosind decoratori în Python
- Memorizare JavaScript
