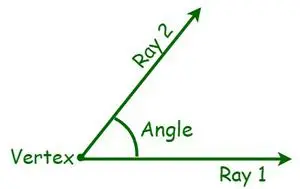
În geometrie, un unghi este o măsură esențială a unei forme geometrice. Un unghi este definit ca gradul de rotație în jurul punctului de intersecție dintre două linii sau plane care sunt necesare pentru a aduce una în corespondență cu cealaltă. Există diferite tipuri de unghiuri, bazate pe măsurarea unui unghi. Se măsoară în grade sau radiani. Un unghi este o formă formată din două linii sau raze care se depărtează de un punct comun numit vârf. Când două raze sunt intersectate, adică atunci când semi-linii sunt proiectate cu un punct final comun, se formează un unghi. Acum, punctele finale comune sunt numite vârfuri, în timp ce razele sunt cunoscute ca brațe.
Tipuri de unghiuri

- Unghi ascutit: Un unghi acut este un unghi care este mai mare de 0 grade și mai mic de 90 de grade, adică variază de la 0° la 90° (ambele exclusiv).
- Unghi drept: Un unghi drept este denumit unghiul care măsoară exact 90 de grade.
- Unghi obtuz: Un unghi obtuz este un unghi care este mai mare de 90 de grade și mai mic de 180 de grade, adică variază de la 90 ° la 180 ° (ambele exclusiv).
- Unghi drept: Un unghi drept este denumit un unghi care măsoară exact 180 de grade.
- Unghiul reflex: Un unghi reflex este un unghi care este mai mare de 180 de grade și mai mic de 360 de grade, adică variază de la 180 ° la 360 ° (ambele exclusiv).
- Un unghi complet sau rotație completă: Un unghi complet este denumit unghiul care măsoară exact 360 de grade.
Există și alte tipuri de unghiuri, cum ar fi unghiuri complementare, unghiuri suplimentare și unghiuri adiacente și neadiacente.
- Unghiuri complementare: Se spune că două unghiuri sunt complementare dacă suma lor este un unghi drept, adică 90°.
- Unghiuri suplimentare: Se spune că două unghiuri sunt suplimentare dacă suma lor este egală cu 180°.
- Unghiuri adiacente: Se spune că două unghiuri sunt adiacente dacă au un vârf comun și un braț comun.
- Unghiuri neadiacente: Se spune că două unghiuri nu sunt adiacente dacă nu au un vârf comun și un braț comun.
Formula pentru găsirea unghiurilor
Există diferite tipuri de formule pentru găsirea unui unghi; unele dintre ele sunt formula unghiului central, formula unghiului dublu, formula semiunghiului, formula unghiului compus, formula unghiului interior etc.
- Folosim formula unghiului central pentru a determina unghiul unui segment realizat într-un cerc.
- Folosim formula sumei unghiurilor interioare pentru a determina unghiul lipsă dintr-un poligon.
- Folosim rapoartele trigonometrice pentru a găsi unghiul lipsă al unui triunghi dreptunghic.
- Folosim legea sinusurilor sau legea cosinusurilor pentru a găsi unghiul lipsă al unui triunghi non-unghi drept.
Numele formulei | Formulă | Cum să găsești un unghi necunoscut? |
|---|---|---|
| Formula unghiului central Citirea fișierului csv în java | θ =(s × 360°)/2prAici, s este lungimea arcului și r este raza cercului | Înlocuiți valorile lungimii arcului și ale razei cercului pentru a determina unghiul unui segment format într-un cerc. |
| Suma unghiurilor interioare Formula | 180°(n-2)Aici, n este numărul de laturi ale unui poligon | Pentru a determina unghiul interior necunoscut al unui poligon, mai întâi, calculați suma tuturor unghiurilor interioare folosind această formulă și apoi scădeți suma tuturor unghiurilor cunoscute din rezultat. |
| Raporturi trigonometrice | sin θ = latura opusă/ipotenuzăcos θ = latura adiacentă/ipotenuzătan θ = latura opusă/latura adiacentă | În funcție de cele două laturi disponibile ale unui triunghi dreptunghic, alegeți unul dintre aceste rapoarte trigonometrice pentru a găsi unghiul necunoscut. |
| Legea Sinurilor | a/sin A = b/sin B = c/sin CAici A, B și C sunt unghiurile interioare ale unui triunghi și a, b și c sunt laturile lor opuse. | Când cunoaștem două laturi și un unghi neinclus (sau) două unghiuri și o latură neinclusă, atunci legea sinusurilor poate fi folosită pentru a determina unghiurile necunoscute ale unui triunghi. |
| Legea cosinusurilor | A2= b2+ c2– 2bc cos Ab2= c2+ a2– 2ca cos Bc2= a2+ b2– 2ab cos CAici A, B și C sunt unghiurile interioare ale unui triunghi și a, b și c sunt laturile lor opuse. | Când cunoaștem trei laturi (sau) două laturi și un unghi inclus, atunci legea cosinusurilor poate fi folosită pentru a determina unghiurile necunoscute ale unui triunghi. |
Exemple de întrebări
Întrebarea 1: Găsiți unghiul la vârful B al triunghiului dat folosind una dintre formulele trigonometrice pentru găsirea unghiurilor.

Soluţie:
Dat,
BC = 3 unități = Latura adiacentă a lui θ.
AC = 4 unități = Partea opusă a lui θ.
scorțișoară vs mateÎn acest caz, cunoaștem atât laturile opuse, cât și cele adiacente ale lui θ. Prin urmare, putem folosi formula tangentei pentru a găsi θ.
⇒ tan θ = latura opusă/latura adiacentă
⇒ tan θ = 4/3
⇒ θ = tan-1(4/3) ⇒ θ = 53,1°
Prin urmare, unghiul la vârful B este de 53,1°.
Întrebarea 2: Aflați unghiurile de la vârfurile X și Y, dacă ∠Z = 35° și x = 3 inchi, y = 8 inci și z = 3,5 inci.

Soluţie:
Dat,
∠Z = 35° și x = 6 inchi, y = 3 inci și z = 3,5 inci
Deoarece cunoaștem toate cele trei laturi și un unghi, putem folosi formula regulii sinusului.
Din formula regulii sinusului avem
x/sin X = y/sin Y = z/sin Z
Acum,
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/fără Y = 3,5/0,574 {Deoarece, sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = păcat−1(0,492) = 29,47°
Știm că suma a trei unghiuri dintr-un triunghi este 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Prin urmare, ∠X = 115,53° și ∠Y = 29,47°.
Întrebarea 3: Calculați al cincilea unghi interior al unui pentagon dacă patru dintre unghiurile sale interioare sunt de 110°, 85°, 136° și 105°.
Soluţie:
Numărul de laturi ale unui pentagon (n) = 5.
git rebaseAcum, suma tuturor celor 5 unghiuri interioare ale unui pentagon = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Suma celor 4 unghiuri interioare date = 110°+ 85°+ 136°+ și 105°= 436°.
Deci, al cincilea unghi interior = 540° – 436° = 104°
Astfel, al cincilea unghi interior al unui pentagon este de 104°.
Întrebarea 4: Determinați valoarea lui y și, de asemenea, măsura unghiurilor din figura dată.

Soluţie:
Din figura dată, putem observa că (4y – 6)° și (3y + 5)° sunt unghiuri complementare, adică suma (4y – 6)° și (3y + 5)° este 90 °.
⇒ (4y – 6)° + (3y + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Acum, (4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Întrebarea 5: Găsiți unghiul la vârful Q în triunghiul dat folosind una dintre formulele pentru găsirea unghiurilor.

Soluţie:
Dat fiind, p = QR = 6 cm, q = PR = 9 cm și r = PQ = 7 cm.
Deoarece cunoaștem toate cele trei laturi și un unghi, putem folosi formula regulii cosinus pentru a găsi vârful unghiului Q.
⇒ q2= p2+ r2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6)(7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
comutați java⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Prin urmare, unghiul la vârful Q, ∠Q = 92,72°.
Întrebarea 6: Calculați unghiul unui segment format într-un cerc dacă lungimea arcului este de 12π și raza este de 9 cm.
Soluţie:
Dat,
Lungimea arcului = 12π
Raza (r) = 9 cm
Acum, formula unghiului este:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
Prin urmare, unghiul este de 240°.
