O prismă este o figură solidă tridimensională cu două capete identice. Este alcătuit din laturi plate, baze similare și secțiuni transversale egale. Fețele sale sunt paralelograme sau dreptunghiuri fără baze. O astfel de prismă care are trei fețe dreptunghiulare și două baze triunghiulare paralele se numește prismă triunghiulară. Bazele triunghiulare sunt conectate prin fețe laterale care sunt paralele între ele.
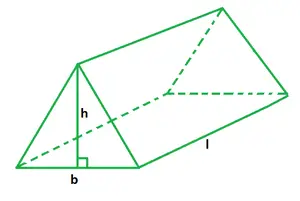
Volumul unei formule de prisme triunghiulare
Volumul unei prisme triunghiulare este definit ca spațiul din interiorul acesteia sau spațiul umplut de ea. Cunoașterea ariei bazei și a înălțimii unei prisme triunghiulare este tot ceea ce este necesar pentru a calcula volumul acesteia. Volumul unei prisme triunghiulare este egal cu produsul dintre aria bazei și înălțimea prismei, cunoscută și sub numele de lungimea prismei. Aria bazei unei prisme triunghiulare este egală cu jumătate din produsul bazei triunghiulare și altitudinea acesteia.
Formulă
V = (1/2) × b × h × l
Unde,
b este baza triunghiulară,
h este altitudinea prismei,
l este lungimea prismei.
Exemple de probleme
Problema 1. Aflați volumul unei prisme triunghiulare dacă baza ei este de 6 cm, altitudinea este de 8 cm și lungimea este de 12 cm.
Soluţie:
Avem b = 6, h = 8 și l = 12.
numărul armstrongFolosind formula pe care o avem,
V = (1/2) × b × h × l
= (1/2) × 6 × 8 × 12
= 3 × 8 × 12
exemple de automate dfa= 288 cu. cm
Problema 2. Aflați volumul unei prisme triunghiulare dacă baza ei este de 5 cm, altitudinea este de 7 cm și lungimea este de 8 cm.
Soluţie:
Avem b = 5, h = 7 și l = 8.
Folosind formula pe care o avem,
V = (1/2) × b × h × l
= (1/2) × 5 × 7 × 8
= 5 × 7 × 4
= 140 cu. cm
Problema 3. Aflați lungimea prismei triunghiulare dacă baza ei este de 6 cm, altitudinea este de 9 cm și volumul este de 98 cu. cm.
Soluţie:
Avem b = 6, h = 9 și V = 98.
Folosind formula pe care o avem,
V = (1/2) × b × h × l
=> 98 = (1/2) × 6 × 9 × l
citește fișierul excel în java=> 196 = 27l
=> l = 196/27
=> l = 7,25 cm
Problema 4. Aflați altitudinea prismei triunghiulare dacă baza ei este de 8 cm, lungimea este de 14 cm și volumul este de 504 cu. cm.
Soluţie:
Avem, b = 8, l = 14 și V = 504.
Folosind formula pe care o avem,
V = (1/2) × b × h × l
=> 504 = (1/2) × 8 × h × 14
=> 504 = 56h
=> h = 504/56
=> h = 9 cm
Problema 5. Aflați aria bazei prismei triunghiulare dacă lungimea acesteia este de 18 cm, înălțimea este de 10 cm și volumul este de 450 cu. cm.
Soluţie:
Avem, l = 18, h = 10 și V = 450.
Folosind formula pentru volum avem,
V = (1/2) × b × h × l
=> 450 = (1/2) × b × 10 × 18
derivat parțial în latex=> 450 = 90b
=> b = 450/90
=> b = 5 cm
Prin urmare, aria bazei triunghiulare este,
A = (1/2) × b × h
= (1/2) × 5 × 10
= 25 cm patrati
