În acest articol, vom discuta despre traversarea arborilor în structura de date. Termenul „tree tree” înseamnă parcurgerea sau vizitarea fiecărui nod al unui arbore. Există o singură modalitate de a parcurge structura liniară de date, cum ar fi lista legată, coada de așteptare și stiva. Întrucât, există mai multe moduri de a traversa un copac care sunt enumerate după cum urmează -
- Precomandă traversare
- Parcurs în ordine
- Traversare prin comanda postala
Deci, în acest articol, vom discuta despre tehnicile enumerate mai sus de traversare a unui copac. Acum, să începem să discutăm despre modalitățile de traversare a copacilor.
Precomandă traversare
Această tehnică urmează politica „rădăcină stânga dreapta”. Înseamnă că primul nod rădăcină este vizitat după ce subarborele din stânga este traversat recursiv și, în final, subarborele din dreapta este parcurs recursiv. Deoarece nodul rădăcină este parcurs înainte (sau înainte) subarborele din stânga și din dreapta, se numește traversare preordine.
Deci, într-o traversare a precomenzii, fiecare nod este vizitat înaintea ambilor subarbori.
Aplicațiile traversării precomenzilor includ -
- Este folosit pentru a crea o copie a arborelui.
- Poate fi folosit și pentru a obține expresia prefixului unui arbore de expresii.
Algoritm
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Exemplu
Acum, să vedem exemplul tehnicii de traversare a precomenzii.
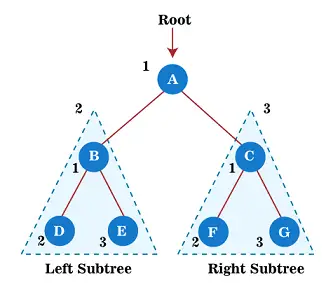
Acum, începeți să aplicați traversarea precomenzii pe arborele de mai sus. În primul rând, traversăm nodul rădăcină A; după aceea, treceți la subarborele din stânga B , care va fi parcurs și în precomanda.
Deci, pentru subarborele din stânga B, mai întâi, nodul rădăcină B este străbătută în sine; după aceea, subarborele său din stânga D este străbătută. Din moment ce nod D nu are copii, treceți în subarborele din dreapta ȘI . Deoarece nodul E nici nu are copii, parcurgerea subarborelului din stânga al nodului rădăcină A este finalizată.
diferența dintre firmă și companie
Acum, deplasați-vă spre subarborele din dreapta al nodului rădăcină A care este C. Deci, pentru subarborele din dreapta C, mai întâi nodul rădăcină C s-a străbătut pe sine; după aceea, subarborele său din stânga F este străbătută. Din moment ce nod F nu are copii, treceți în subarborele din dreapta G . Deoarece nodul G nu are nici copii, parcurgerea subarborelului din dreapta al nodului rădăcină A este finalizată.
Prin urmare, toate nodurile arborelui sunt parcurse. Deci, rezultatul traversării precomenzii arborelui de mai sus este -
A → B → D → E → C → F → G
Pentru a afla mai multe despre parcurgerea precomenzilor în structura de date, puteți urma linkul Precomandă traversare .
java public vs privat
Parcursul prin comanda postala
Această tehnică urmează politica „rădăcină stânga-dreapta”. Înseamnă că primul subarboresc din stânga al nodului rădăcină este parcurs, după care traversează recursiv subarborele din dreapta și, în final, este parcurs nodul rădăcină. Deoarece nodul rădăcină este traversat după (sau postează) subarborele din stânga și din dreapta, se numește traversare post-ordine.
Deci, într-o traversare post-comandă, fiecare nod este vizitat după ambii subarbori.
Aplicațiile traversării post-comandă includ:
- Este folosit pentru a șterge arborele.
- Poate fi folosit și pentru a obține expresia postfixă a unui arbore de expresii.
Algoritm
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Exemplu
Acum, să vedem exemplul tehnicii de traversare post-comandă.

Acum, începeți să aplicați traversarea postcomandă pe arborele de mai sus. În primul rând, parcurgem subarborele din stânga B care va fi parcurs în postordine. După aceea, vom străbate subarborele din dreapta C în post-ordine. Și, în sfârșit, nodul rădăcină al arborelui de mai sus, adică, A , este străbătută.
Deci, pentru subarborele din stânga B, mai întâi, subarborele său din stânga D este străbătută. Din moment ce nod D nu are copii, traversați subarborele din dreapta ȘI . Deoarece nodul E nici nu are copii, treceți la nodul rădăcină B. După parcurgerea nodului B, parcurgerea subarborelui stâng al nodului rădăcină A este finalizată.
Acum, deplasați-vă către subarborele din dreapta al nodului rădăcină A care este C. Deci, pentru subarborele din dreapta C, mai întâi subarborele din stânga F este străbătută. Din moment ce nod F nu are copii, traversați subarborele din dreapta G . Deoarece nodul G, de asemenea, nu are copii, prin urmare, în sfârșit, nodul rădăcină al subarborelui drept, adică, C, este străbătută. Parcurgerea subarborelui drept al nodului rădăcină A este finalizată.
În cele din urmă, traversați nodul rădăcină al unui arbore dat, adică A . După parcurgerea nodului rădăcină, traversarea post-comandă a arborelui dat este finalizată.
Prin urmare, toate nodurile arborelui sunt parcurse. Deci, rezultatul traversării post-comandă a arborelui de mai sus este -
D → E → B → F → G → C → A
Pentru a afla mai multe despre traversarea post-comandă în structura de date, puteți urma linkul Traversare prin comanda postala .
shreya ghoshal
Parcurs în ordine
Această tehnică urmează politica „rădăcină stângă dreapta”. Înseamnă că primul subarboresc din stânga este vizitat după ce acel nod rădăcină este traversat și, în final, subarborele din dreapta este parcurs. Pe măsură ce nodul rădăcină este traversat între subarborele din stânga și din dreapta, acesta este numit traversare în ordine.
Deci, în traversarea în ordine, fiecare nod este vizitat între subarborii săi.
Aplicațiile traversării în ordine includ -
- Este folosit pentru a obține nodurile BST în ordine crescătoare.
- Poate fi folosit și pentru a obține expresia prefixului unui arbore de expresii.
Algoritm
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Exemplu
Acum, să vedem exemplul tehnicii de traversare Inorder.

Acum, începeți să aplicați traversarea în ordine pe arborele de mai sus. În primul rând, traversăm subarborele din stânga B care vor fi parcurse in ordine. După aceea, vom străbate nodul rădăcină A . Și, în sfârșit, subarborele potrivit C este străbătută în ordine.
Deci, pentru subarborele din stânga B , în primul rând, subarborele său din stânga D este străbătută. Din moment ce nod D nu are copii, asa ca dupa ce il traverseaza, nod B va fi parcurs și, în sfârșit, subarborele din dreapta al nodului B, adică ȘI , este străbătută. De asemenea, nodul E nu are copii; prin urmare, parcurgerea subarborelului stâng al nodului rădăcină A este finalizată.
După aceea, traversați nodul rădăcină al unui arbore dat, adică A .
împărțit prin șir de caractere java
În cele din urmă, deplasați-vă către subarborele din dreapta al nodului rădăcină A care este C. Deci, pentru subarborele drept C; în primul rând, subarborele său stâng F este străbătută. Din moment ce nod F nu are copii, nod C va fi parcurs și, în sfârșit, un subarboresc drept al nodului C, adică G , este străbătută. De asemenea, nodul G nu are copii; prin urmare, parcurgerea subarborelui drept al nodului rădăcină A este finalizată.
Pe măsură ce toate nodurile arborelui sunt parcurse, parcurgerea în ordine a arborelui dat este finalizată. Ieșirea traversării în ordine a arborelui de mai sus este -
D → B → E → A → F → C → G
Pentru a afla mai multe despre traversarea în ordine în structura datelor, puteți urma linkul Traversare în ordine .
Complexitatea tehnicilor de traversare a arborilor
Complexitatea în timp a tehnicilor de traversare a arborilor discutate mai sus este Pe) , Unde 'n' este dimensiunea arborelui binar.
În timp ce complexitatea spațială a tehnicilor de traversare a copacilor discutate mai sus este O(1) dacă nu luăm în considerare dimensiunea stivei pentru apelurile de funcții. În caz contrar, complexitatea spațială a acestor tehnici este Oh) , Unde 'h' este înălțimea copacului.
Implementarea Tree traversal
Acum, să vedem implementarea tehnicilor discutate mai sus folosind diferite limbaje de programare.
Program: Scrieți un program pentru a implementa tehnici de traversare a arborilor în C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Ieșire
program c pentru compararea șirurilor

Program: Scrieți un program pentru a implementa tehnici de traversare a arborilor în C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Ieșire

Program: Scrieți un program pentru a implementa tehnici de traversare a arborilor în C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Ieșire
După executarea codului de mai sus, rezultatul va fi -

Concluzie
În acest articol, am discutat despre diferitele tipuri de tehnici de traversare a arborilor: traversare precomanda, traversare în ordine și traversare postcomandă. Am văzut aceste tehnici împreună cu algoritm, exemplu, complexitate și implementare în C, C++, C# și java.
Deci, asta e totul despre articol. Sper să vă fie de ajutor și informativ.
