Trapez în matematică: Un trapez este un poligon cu patru laturi, adică este un patrulater. Trapezul provine din cuvântul grecesc trapez care înseamnă masă. Este un patrulater complex. Un trapez este un patrulater special cu o singură pereche de laturi paralele. Un trapez este o formă bidimensională care apare ca un tabel.
Un trapez are patru laturi și patru vârfuri. Vedem forma trapezului în viața noastră de zi cu zi și este una dintre cele mai comune forme. În acest articol, vom afla despre ce este trapezul în matematică, proprietățile sale, formulele, exemplele și tipurile de trapez, împreună cu câteva exemple rezolvate ale acestuia.
Cuprins
- Ce este un trapez la matematică?
- Tipuri de trapez
- Trapez neregulat
- Proprietățile Trapezului
- Formula trapezului
- Zona de Formula Trapez
- Formula perimetrului trapezului
- Diferența dintre trapez și trapez
- Unghiurile trapezului
- Diagonala Trapezului
- Exemple de trapez
Ce este un trapez la matematică?
Un trapez este un patrulater bidimensional, în formă închisă, având o pereche de laturi opuse paralele. Laturile paralele ale unui trapez se numesc baze, iar laturile neparalele ale unui trapez se numesc catete. Trapezul are patru laturi și patru colțuri. A paralelogram se mai numește și trapez cu două laturi paralele.
Definiția trapezului
Un trapez este un patrulater (un poligon cu patru laturi) cu cel puțin o pereche de laturi paralele. Aceste laturi paralele sunt denumite bazele trapezului, iar celelalte două laturi sunt numite picioare, care nu sunt neapărat paralele.
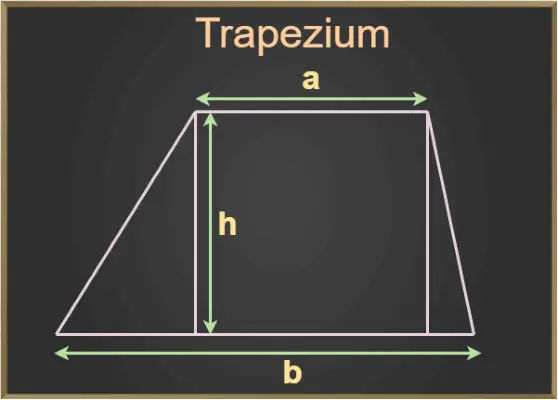
În figura de mai sus, a și b sunt bazele trapezului și h este înălțimea trapezului.
Forma trapezului
Trapezul este a patrulater adică poligon cu patru laturi. Un trapez are patru laturi cu o pereche de laturi opuse paralele între ele. Forma trapezului este foarte comună și vedem diverse lucruri în viața noastră de zi cu zi care sunt asemănătoare cu trapezul. Câteva exemple din viața reală de trapez observate de noi sunt mesele în formă de trapez, plăcile, tablourile și altele.
Tipuri de trapez
Pe baza laturilor și a unghiurilor, trapezul este de trei tipuri:
- Trapezul Scalen
- Trapez isoscel
- Trapezul drept

Trapez isoscel
Trapezul care are o lungime egală a picioarelor se numește trapez isoscel, adică într-un trapez isoscel, cele două laturi neparalele sunt egale.
Trapezul Scalen
Un trapez cu toate laturile nu sunt egale se numește trapez scalen. Într-un trapez scalen, nu există două unghiuri egale.
Trapezul drept
Un trapez care are o pereche în unghi drept, adiacent unul altuia este cunoscut sub numele de trapez drept.
Trapez neregulat
Un trapez are o pereche de laturi paralele, iar celelalte două laturi sunt neparalele. Într-un trapez obișnuit, celelalte două laturi neparalele sunt egale, dar în cazul unui trapez neregulat cele două laturi opuse neparalele sunt inegale.
Proprietățile Trapezului
Există diverse proprietăți ale trapezului, dintre care unele sunt după cum urmează:
- Laturi paralele: Un trapez are două laturi paralele, care se numesc baze. Exemplu: Laturile AB și CD sunt paralele între ele, prezentate în figură.
- Laturi neparalele: Laturile neparalele ale unui trapez se numesc picioare, iar picioarele unui trapez nu sunt egale ca lungime. Exemplu: Laturile AD și BC sunt laturi neparalele ale trapezului.
- Înălțime sau altitudine: Distanța perpendiculară dintre baze se numește înălțimea sau altitudinea trapezului. În diagrama de mai sus, h este înălțimea trapezului.
- Suma unghiurilor
- Unghiurile interioare adiacente într-un trapez însumează până la 180°. Exemplu: Există două perechi de unghiuri co-interioare. O pereche este ∠ A și ∠ D, în timp ce cealaltă pereche este ∠ B și ∠ C. Suma fiecărei perechi de unghiuri co-interioare este 180°.
- Suma tuturor unghiurilor interioare dintr-un trapez este întotdeauna 360°. Exemplu : În figura ∠A+∠D este 180° și ∠B+∠C este 180°. Prin urmare ∠A+∠D +∠B+∠C = 360°.
- Median: Mediana unui trapez este segmentul de linie care leagă punctele medii ale picioarelor. Mediana este paralelă cu bazele și lungimea sa este media lungimilor bazelor.
- Trapezul are exact o pereche de laturi opuse care sunt paralele.
Formula trapezului
Formulele importante ale unui trapez sunt:
- Zona Trapezului = ½ (Suma laturilor paralele) × (Distanța dintre laturile paralele)
- Perimetrul Trapezului = Suma tuturor celor patru laturi
Zona de Formula Trapez
Trapezul are două laturi paralele a, respectiv b unități, iar altitudinea sa este h.
Acum aria trapezului poate fi calculată prin găsirea mediei bazelor și înmulțirea rezultatului acesteia cu altitudinea. Prin urmare,
Zona Trapezului = ((a +b)/2) × h
Unde,
- A și b sunt Bazele Trapezului
- h este Altitudinea
Zona trapezului isoscel
Fie a și b lungimea laturilor paralele ale unui trapez ABCD, unde a și b sunt bazele trapezului și a>b.
Acum, deoarece este un trapez isoscel, c este lungimea ambelor laturi neparalele și h este înălțimea trapezului.
Acum, AB = a, CD = b, BC = AD = c
comparare șiruri java
În Triunghi dreptunghic , AED
Lungimea perpendicularei, h = √(c 2 – (a-b) 2 ) [folosind Teorema lui Pitagora ]….(1)
Acum,
Aria = ½ × Suma laturilor paralele × Înălțimea trapezului
Aria = ½ × (a+b) × h
Folosind ecuația (1)
Zona trapezului isoscel = 1/2 × [√(c 2 – (a-b) 2 ) (a+b)]
Formula perimetrului trapezului
Perimetrul unui trapez este dat prin calcularea sumei tuturor laturilor sale. Prin urmare,
Perimetrul trapezului = AB + BC + CD + AD
Unde, AB, BC, CD și ANUNȚ sunt Laturile Trapezului
Perimetrul trapezului isoscel
Dacă într-un trapez isoscel a și b sunt lungimile laturilor paralele, adică bazele și c este lungimea a două laturi egale neparalele, atunci perimetrul este dat de:
Perimetrul = a + b + 2c
Unde,
- A , b sunt Bazele Trapezului
- c este partea egală a trapezului
Diferența dintre trapez și trapez
În termeni generali, atât Trapezul, cât și Trapezul sunt la fel, dar diferența constă în țara lor de origine.
- Trapez este de origine britanică, este un poligon cu patru laturi și o figură bidimensională are exact o pereche de laturi paralele opuse una față de cealaltă. În India, urmăm engleza britanică, prin urmare, este folosit cuvântul Trapezium.
- Trapez este de origine americană, este, de asemenea, un poligon cu patru laturi cu o pereche de laturi paralele opuse una față de cealaltă. Laturile paralele sunt bazele și alte două laturi neparalele se numesc picioarele trapezului.
Unghiurile trapezului
Trapezul este un patrulater și suma tuturor unghiurilor unui patrulater este de 360 de grade. Deci suma tuturor unghiurilor interioare ale trapezului este de 360 de grade.
Pentru orice trapez regulat, adică trapezul în care laturile neparalele sunt egale cu unghiurile alăturate formate între linia paralelă și linia neparalelă este egal. Astfel, suma acestor două unghiuri este suplimentară.
Să luăm un exemplu pentru a susține acest concept pentru un trapez isoscel ABCD dacă AB este paralel cu CD și AD este egal cu CD, atunci știm că ∠A = ∠B și ∠C = ∠D atunci,
∠A + ∠B + ∠C + ∠D = 360°
Aici, ∠A = ∠B și ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
În mod similar, (∠B + ∠D) = 180°
Diagonala Trapezului
Trapezul este un tip special de patrulater; astfel, trapezul are și două diagonale. Diagonalele unui trapez nu au lungimi egale, spre deosebire de alte patrulatere, cum ar fi dreptunghiurile sau paralelogramele. Diagonalele trapezului nu au lungimi egale, iar lungimile diagonalelor depind de lungimile bazelor și de unghiurile trapezului.
Exemplu: Pentru un trapez isoscel ABCD, unghiul de bază ∠A este de 80°, apoi găsiți celălalt unghi ∠C.
Știm că pentru un trapez isoscel ABCD,
(∠A + ∠C) = 180°
Având în vedere, ∠A = 80°
poate o clasă extinde mai multe claseAcum, 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
Astfel, Unghiul necesar ∠C este 100°
Formulele Trapezului – Aria și Perimetrul Trapezului
Formulele legate de trapez sunt rezumate în următorul tabel:
| Proprietate | Formulă |
|---|---|
| Zonă | 1/2 × ( A + b ) × h |
| Zona (trapez isoscel) | 1/2 × [√(c2– (a-b)2) (a+b)] |
| Perimetru | A + b + c + d |
| Perimetrul (trapez isoscel) | A + b + 2 c |
| Median | (A + b)/2 |
Oamenii citesc și:
- Romb
- Triunghi
- Care este formula pentru a găsi aria trapezului?
Exemple de trapez
Exemplul 1: Găsiți a patra latură a trapezului, dacă celelalte trei laturi au 8 cm, 12 cm și 16 cm, iar perimetrul este de 40 cm.
Soluţie:
Perimetrul este dat ca suma tuturor laturilor sale. Fie lungimea o necunoscută unități „x”.
Perimetrul = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Astfel, lungimea laturii necunoscute este de 4 cm
Exemplul 2: Un trapez are laturi paralele de lungimi de 15 cm și 11 cm și laturi neparalele de lungime de 5 cm fiecare. Calculați perimetrul trapez.
Soluţie:
Este un trapez isoscel deoarece se menționează clar că laturile neparalele cu lungimea de 5 cm fiecare sunt egale.
Conform Trapezului Isoscel, dacă două laturi neparalele ale Trapezului sunt de lungime egală, atunci este cunoscut sub numele de Trapez Isoscel.
Dat,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Perimetrul = a + b + 2c
P = 15 + 11 + 2(5)
P = 15 + 11 + 10
P = 36 cm
Exemplul 3: Găsiți perimetrul unui trapez ale cărui laturi sunt de 12 cm, 14 cm, 16 cm și 18 cm.
Soluţie:
P = Suma tuturor laturilor
P = 12 + 14 + 16 + 18
P = 60 cm
Prin urmare, perimetrul trapezului este de 60 cm
Exemplul 4: Găsiți aria trapezului, în care suma laturilor paralele este de 60 cm, iar înălțimea sa este de 10 cm.
Soluţie:
Dat,
- Suma laturilor paralele 60 cm
- înălțime, h = 10 cm
Aria trapezului, A = 1/2 × Suma laturilor paralele × Distanța dintre laturile paralele
Înlocuirea valorilor date,
A =1/2×60×10
A = 30×10
A = 300 cm2
Prin urmare, Aria trapezului = 300 cm2
Practicați probleme pe trapez în matematică
1. Aflați aria unui trapez cu bazele de 10 cm și 15 cm și înălțimea de 6 cm.
2. Un trapez are o suprafață de 54 de metri pătrați. Dacă una dintre baze are 12 metri lungime și înălțimea este de 6 metri, găsiți lungimea celeilalte baze.
3. Calculați perimetrul unui trapez cu baze de 8 cm și 14 cm, iar laturile neparalele de 5 cm și 7 cm.
4. Determinați lungimea segmentului mijlociu într-un trapez unde bazele măsoară 18 cm și 30 cm.
5. Într-un trapez isoscel, unghiurile de la o bază sunt fiecare de 45 de grade. Găsiți măsurile unghiurilor de la cealaltă bază. Să presupunem că trapezul nu este un trapez corect.
Rezumat – Trapez în matematică
Un trapez este un poligon cu patru laturi, sau patrulater, caracterizat prin faptul că are o pereche de laturi paralele numite baze, în timp ce celelalte două laturi, cunoscute sub numele de catete, nu sunt paralele. Des întâlnit în obiectele de zi cu zi precum mesele, trapezul se remarcă prin proprietățile sale geometrice: are o înălțime, care este distanța perpendiculară dintre baze, și o mediană care conectează punctele medii ale laturilor neparalele și este paralelă cu bazele.
Aria unui trapez se calculează prin media lungimii bazelor și înmulțirea cu înălțimea, în timp ce perimetrul său este suma tuturor laturilor sale. Cu diferite clasificări, cum ar fi scalen, isoscele și trapeze drepte, fiecare cu proprietăți unice de latură și unghi, trapezele sunt fundamentale atât în aplicațiile practice, cât și în teoria geometrică.
Întrebări frecvente despre Trapez în matematică
Ce este forma trapezului?
Trapezul este un patrulater în care o pereche de drepte este întotdeauna paralelă. Seamănă cu forma unei mese. Numele său este luat din cuvântul grecesc trapez care înseamnă masă.
Câte tipuri de trapez?
Există două tipuri de trapez,
- Trapez obișnuit: În care cealaltă pereche de linii sunt egale.
- Trapez neregulat: În care cealaltă pereche de linii nu sunt egale.
Câte laturi paralele are un trapez?
Știm că trapezul este un patrulater cu o pereche de laturi paralele. Astfel, un trapez are o pereche de linii paralele (laturi).
Un trapez poate fi considerat un patrulater?
A are patru laturi, patru vârfuri și patru unghiuri. Prin urmare, poate fi considerat un patrulater, suma tuturor celor patru unghiuri interioare ale unui trapez este de 360 de grade.
f-string python
Un pătrat poate fi numit trapez?
Un trapez este un patrulater cu o singură pereche de laturi paralele, iar celelalte două laturi sunt neparalele. Dar în cazul unui Pătrat, are două perechi de laturi paralele, prin urmare, nu poate fi considerat un Trapez.
Diagonalele unui trapez sunt întotdeauna egale?
Diagonalele unui trapez pot să nu fie egale. În cazul unui poligon regulat, diagonalele sunt egale, dar acest lucru nu este adevărat în cazul unui poligon neregulat.
Care sunt proprietățile unui trapez?
5 proprietăți ale unui trapez sunt:
- În trapez, bazele sunt paralele între ele.
- Un trapez are unghiuri adiacente suplimentare.
- Doar o pereche de laturi opuse sunt paralele.
- Suma tuturor unghiurilor interioare dintr-un trapez este întotdeauna 360°.
- Linia care unește punctul de mijloc al laturilor neparalele este întotdeauna paralelă cu bazele.
