Sortare topologică pentru Graficul aciclic direcționat (DAG) este o ordonare liniară a vârfurilor astfel încât pentru fiecare muchie direcționată u-v, vârf în vine înainte de în în comandă.
Notă: Sortarea topologică pentru un grafic nu este posibilă dacă graficul nu este a ZI .
Exemplu:
Practică recomandatăSoluție bazată pe DFS pentru a găsi o sortare topologică a fost deja discutat.Intrare: Grafic :
Exemplu
Ieșire: 5 4 2 3 1 0
Explicaţie: Primul vârf din sortarea topologică este întotdeauna un vârf cu un grad de 0 (un vârf fără muchii de intrare). O sortare topologică a graficului următor este 5 4 2 3 1 0. Poate exista mai mult de o sortare topologică pentru un grafic. O altă sortare topologică a graficului următor este 4 5 2 3 1 0.
Ordinea topologică poate să nu fie unică:
Sortarea topologică este o problemă de dependență în care finalizarea unei sarcini depinde de finalizarea mai multor alte sarcini a căror ordine poate varia. Să înțelegem acest concept printr-un exemplu:
Să presupunem că sarcina noastră este să ajungem la școala noastră și pentru a ajunge acolo, mai întâi trebuie să ne îmbrăcăm. Dependența de a purta haine este prezentată în graficul de dependență de mai jos. De exemplu, nu poți purta pantofi înainte de a purta șosete.
incearca sa prinzi java
Din imaginea de mai sus ați fi realizat deja că există mai multe moduri de a vă îmbrăca, imaginea de mai jos arată câteva dintre aceste moduri.
Poți enumera toată ordonarea topologică posibilă de a te îmbrăca pentru graficul de dependență de mai sus?
Algoritm pentru sortarea topologică folosind DFS:
Iată un algoritm pas cu pas pentru sortarea topologică folosind Depth First Search (DFS):
- Creați un grafic cu n vârfuri şi m -margini dirijate.
- Inițializați o stivă și o matrice de dimensiuni vizitată n .
- Pentru fiecare vârf nevizitat din grafic, procedați în felul următor:
- Apelați funcția DFS cu vârful ca parametru.
- În funcția DFS, marcați vârful ca vizitat și apelați recursiv funcția DFS pentru toți vecinii nevizitați ai vârfului.
- Odată ce toți vecinii au fost vizitați, împingeți vârful pe stivă.
- La urma urmei, vârfurile au fost vizitate, scoateți elementele din stivă și adăugați-le la lista de ieșiri până când stiva este goală.
- Lista rezultată este ordinea sortată topologic a graficului.
Ilustrație Algoritmul de sortare topologică:
Imaginea de mai jos este o ilustrare a abordării de mai sus:

Fluxul general de lucru al sortării topologice
Pasul 1:
- Pornim DFS de la nodul 0, deoarece are zero Noduri de intrare
- Împingem nodul 0 în stivă și trecem la nodul următor având un număr minim de noduri adiacente, adică nodul 1.
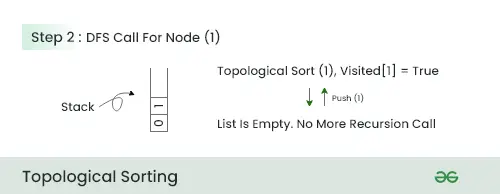
elementele de bază ale javaPasul 2:
- În acest pas, deoarece nu există niciun adiacent acestui nod, împingeți nodul 1 în stivă și treceți la nodul următor.
Pasul 3:
- În acest pas, alegem nodul 2 deoarece are un număr minim de noduri adiacente după 0 și 1.
- Apelăm DFS pentru nodul 2 și împingem toate nodurile care vin în traversare de la nodul 2 în ordine inversă.
- Deci apăsați 3 apoi apăsați 2.
Pasul 4:
- Acum numim DFS pentru nodul 4
- Deoarece 0 și 1 sunt deja prezente în stivă, așa că doar împingem nodul 4 în stivă și revenim.
Pasul 5:
convertiți șirul în obiect json
- În acest pas, deoarece toate nodurile adiacente ale lui 5 sunt deja în stivă, împingem nodul 5 în stivă și revenim.
Pasul 6: Acesta este pasul final al sortării topologice în care scoatem tot elementul din stivă și îl imprimăm în această ordine.
Mai jos este implementarea abordării de mai sus:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vector & vizitat, stiva & Stack) { // Marcați nodul curent ca vizitat vizitat[v] = true; // Recură pentru toate nodurile adiacente pentru (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Împinge vârful curent în stiva care stochează rezultatul Stack.push(v); } // Funcție pentru a efectua Sortarea topologică void Sortare topologică (vector>& adj, int V) { stivă Grămadă; // Stack pentru a stoca vectorul rezultat vizitat(V, fals); // Apelați funcția de ajutor recursiv pentru a stoca // Sortare topologică începând de la toate vârfurile unul câte // unul pentru (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> muchii = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Graficul reprezentat ca un vector de listă de adiacență> adj(V); pentru (auto i : margini) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, boolean[] vizitat, Stack stack) { // Marcați nodul curent ca vizitat vizitat[v] = true; // Recură pentru toate nodurile adiacente pentru (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Împinge vârful curent în stiva care stochează // rezultatul stack.push(v); } // Funcție pentru a efectua Sortarea topologică static void topologicalSort(List> adj, int V) { // Stack pentru a stoca rezultatul Stack stivă = stivă nouă(); boolean[] vizitat = boolean nou[V]; // Apelați funcția de ajutor recursiv pentru a stoca // Sortare topologică începând de la toate vârfurile unul // câte unul pentru (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> margini = new ArrayList(); edges.add(Arrays.asList(0, 1)); edges.add(Arrays.asList(1, 2)); edges.add(Arrays.asList(3, 1)); edges.add(Arrays.asList(3, 2)); // Graficul reprezentat ca o listă de adiacență Listă> adj = new ArrayList(V); pentru (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : margini) { adj.get(i.get(0)).add(i.get(1)); } Sortare topologică(adj, V); } }>>>Python3
C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] vizitat, Stack stack) { // Marcați nodul curent ca vizitat vizitat[v] = true; // Recură pentru toate nodurile adiacente foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Împinge vârful curent în stiva care stochează // stiva de rezultat. Push(v); } // Funcție pentru a efectua Sortarea topologică static void Sortare topologică (List> adj, int V) { // Stack pentru a stoca rezultatul Stack stivă = stivă nouă (); bool[] vizitat = new bool[V]; // Apelați funcția de ajutor recursiv pentru a stoca // Sortare topologică începând de la toate vârfurile unul // câte unul pentru (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Cod driver static void Main(string[] args) { // Numărul de noduri int V = 4; // Lista marginilor> margini = Listă nouă>{ Listă nouă { 0, 1 }, listă nouă { 1, 2 }, listă nouă { 3, 1 }, listă nouă { 3, 2 } }; // Graficul reprezentat ca o listă de adiacență Listă> adj = Listă nouă>(); pentru (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Lista i în margini) { adj[i[0]].Add(i[1]); } TopologicalSort(adj, V); } }>>>Javascript0) { console.log(stack.pop() + ' '); } } // Cod driver (() => { // Numărul de noduri const V = 4; // Muchii const muchii = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Grafic reprezentat ca o listă de adiacență const adj = Array.from({ length: V }, () => []); (i[1]);>>>
Ieșire Topological sorting of the graph: 3 0 1 2>
Complexitatea timpului: O(V+E). Algoritmul de mai sus este pur și simplu DFS cu o stivă suplimentară. Deci, complexitatea timpului este aceeași cu DFS
Spatiu auxiliar: O(V). Spațiul suplimentar este necesar pentru stivă
Sortare topologică folosind BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Pointer către un tablou care conține // liste de adiacență public: Graph(int V); // Constructor void addEdge(int v, int w); // Funcție pentru a adăuga o margine la graficul void topologicalSort(); // afișează un Sort Topologic al // graficul complet }; Graph::Graph(int V) { this->V = V; adj = listă nouă [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Adăugați w la lista lui v. } // Funcția pentru a efectua Sortarea topologică void Graph::topologicalSort() { // Creați un vector pentru a stoca în gradul tuturor vectorului vârfurilor în_grade(V, 0); // Parcurgeți listele de adiacență pentru a completa în_degree de // vârfuri pentru (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; pentru (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Scoateți unul câte unul nodurile din coadă și coadă // vârfurile adiacente dacă gradul adiacent devine 0 în timp ce (!q.empty()) { // Extrageți partea din față a cozii (sau executați scoaterea din coadă) // și adăugați-l la ordine topologică int u = q.front(); q.pop(); top_order.push_back(u); // Iterează prin toate nodurile învecinate // ale nodului u scos din coadă și micșorează gradul lor // cu 1 listă ::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Dacă in-degree devine zero, adăugați-l la coadă dacă (--in_degree[*itr ] == 0) q.push(*itr); numără++; } // Verificați dacă a existat un ciclu if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Lista de adiacență // reprezentarea // a graficului // Constructor Graph(int V) { this.V = V; adj = nou ArrayList[V]; pentru (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = noua Lista Linked(); pentru (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // Scoateți unul câte unul nodurile din coadă și // puneți în coadă nodurile adiacente dacă gradul // adiacent devine 0 în timp ce (!q.isEmpty()) { // Extrageți partea din față a cozii și adăugați-l la // ordinea topologică int u = q.poll(); topOrder.add(u); numără++; // Iterează prin toate nodurile învecinate ale // nodului u scos din coadă și micșorează gradul lor // cu 1 pentru (int w : adj[u]) { // Dacă gradul devine zero, adăugați-l la // coadă dacă (--inGrad[w] == 0) q.add(w); } } // Verificați dacă a existat un ciclu if (count != V) { System.out.println('Graph contains cycle'); întoarcere; } // Imprimă ordinea topologică pentru (int i : topOrder) System.out.print(i + ' '); } } // Cod driver public class Main { public static void main(String[] args) { // Creați un grafic dat în diagrama de mai sus Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println('Urmeaza un sort topologic al graficului dat'); g.topologicalSort(); } }>>>Python3 JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Ieșire
Complexitatea timpului pentru construirea graficului este O(V + E), unde V este numărul de vârfuri și E este numărul de muchii.
Complexitatea timpului pentru efectuarea sortării topologice folosind BFS este, de asemenea, O(V + E), unde V este numărul de vârfuri și E este numărul de muchii. Acest lucru se datorează faptului că fiecare vârf și fiecare muchie sunt vizitate o dată în timpul traversării BFS.
Complexitatea spațiului:
Complexitatea spațiului pentru stocarea graficului folosind o listă de adiacență este O(V + E), unde V este numărul de vârfuri și E este numărul de muchii.
Spațiul suplimentar este utilizat pentru stocarea gradului de vârfuri, care necesită spațiu O(V).
O coadă este utilizată pentru traversarea BFS, care poate conține cel mult V vârfuri. Astfel, complexitatea spațiului pentru coadă este O(V).
noroc
În general, complexitatea spațială a algoritmului este O(V + E) datorită stocării graficului, a tabloului în grad și a cozii.
În rezumat, complexitatea de timp a implementării furnizate este O(V + E), iar complexitatea spațiului este, de asemenea, O(V + E).
Notă: Aici, putem folosi și o matrice în loc de stiva. Dacă se utilizează matricea, imprimați elementele în ordine inversă pentru a obține sortarea topologică.
Avantajele sortării topologice:
- Ajută la programarea sarcinilor sau evenimentelor bazate pe dependențe.
- Detectează ciclurile într-un grafic direcționat.
- Eficient pentru rezolvarea problemelor cu constrângeri de precedență.
Dezavantajele sortării topologice:
- Se aplică numai graficelor aciclice direcționate (DAG), nu sunt potrivite pentru graficele ciclice.
- Poate să nu fie unice, pot exista mai multe ordonări topologice valide.
- Ineficient pentru grafice mari cu multe noduri și muchii.
Aplicații ale sortării topologice:
- Programarea sarcinilor și managementul proiectelor.
- Rezolvarea dependenței în sistemele de management al pachetelor.
- Determinarea ordinii de compilare în sistemele de construcție software.
- Detectarea blocajelor în sistemele de operare.
- Programarea cursurilor în universități.
Articole similare:
- Algoritmul lui Kahn pentru sortarea topologică
- Toate tipurile topologice ale unui grafic aciclic direcționat