Pot fi măsurate trei dimensiuni, lungime, lățime și înălțime, pentru orice obiect pe care îl puteți vedea sau atinge. Există anumite dimensiuni ale casei noastre în care trăim. Ecranul de afișare dreptunghiular/monitorul pe care îl privești are o lățime și o lățime a lungimii sale. Pentru fiecare structură geometrică tridimensională se măsoară suprafața și volumul.
Aria acoperită de suprafața obiectului este aria suprafeței oricărui obiect dat. În timp ce cantitatea de spațiu disponibilă într-un obiect este volumul.
Cuprins
- Suprafață
- Suprafața totală
- Suprafață curbată/Suprafață laterală
- Volum
- Exemple privind suprafețele și volumele
- Întrebări frecvente despre formulele de suprafață și volum
Suprafață
Suprafața și volumul pot fi calculate pentru orice formă geometrică tridimensională (3D). Suprafața oricărei zone este regiunea ocupată de suprafața unui obiect. Volumul este cantitatea de spațiu disponibil într-un obiect. Avem diferite tipuri de forme, cum ar fi o emisferă, sferă, cub, cuboid, cilindru etc. Toate formele tridimensionale au zonă și volum. Dar forme bidimensionale precum pătrate, dreptunghiuri, triunghiuri, cercuri etc.
Aici, în două dimensiuni, putem măsura doar aria. Aria ocupată de un obiect tridimensional de suprafața sa exterioară se numește suprafață. Se măsoară în unități pătrate.
Zona este de două tipuri:
- Suprafața totală
- Suprafață curbată/Suprafață laterală
Suprafața totală
Suprafața care include baza (bazele) și porțiunea curbată corespunde suprafeței totale. Este cantitatea de suprafață închisă de suprafața obiectului. Dacă forma are o bază și o suprafață curbate, deci suma celor două regiuni ar fi aria totală. Suprafața totală poate fi definită ca suprafața totală acoperită de un obiect, inclusiv baza acestuia, precum și partea curbată. Dacă un obiect are atât baza, cât și suprafața curbă, atunci suprafața totală va fi egală cu suma unei baze și a unei zone curbe.
- Suprafața totală este suprafața totală ocupată de un obiect.
- De exemplu, luați ca exemplu un cuboid, cuboidul are 6 fețe, 12 muchii și 8 vârfuri.
Suprafața totală = Suprafața de bază + Suprafața curbă
liste css
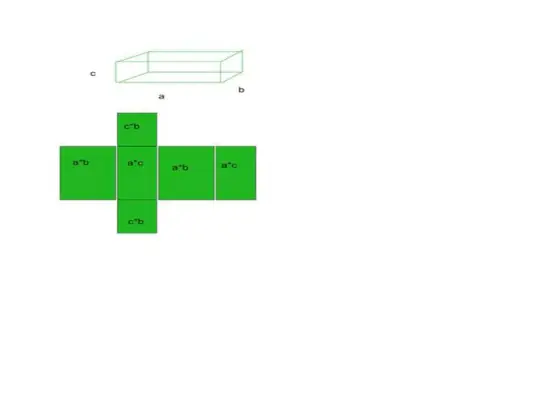
- Suma tuturor acestor 6 zone va fi suprafața noastră totală a formei particulare
Exemplu:
Mai jos este un cuboid având dimensiunea dată ca lungime = 8 cm, lățime = 4 cm și înălțime = 6 cm, găsiți TSA a unui cuboid
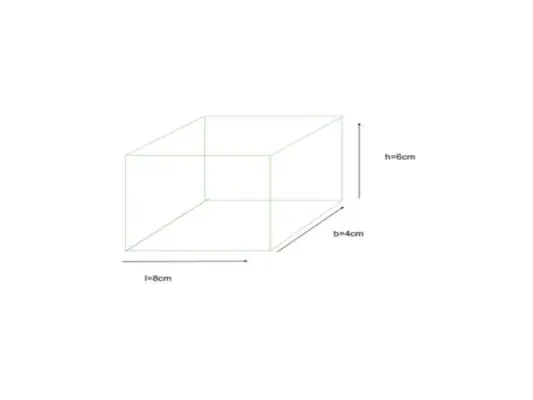
dat l = 8cm, b = 4cm, h = 6cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
TSA al cuboidului este de 208 cm.
Suprafață curbată/Suprafață laterală
Suprafața curbată, cu excepția centrului acesteia, corespunde numai zonei porțiunii curbe a formei (formelor). Pentru forme precum un con, se numește adesea suprafața laterală. Suprafața laterală poate fi definită ca zona care include numai suprafața curbată a unui obiect sau suprafața laterală a unui obiect prin excluderea zonei de bază a unui obiect. Zona de suprafață laterală este cunoscută și sub denumirea de suprafață curbată.
Majoritatea formelor sau obiectelor se referă la suprafața curbată, forma sau cilindrul asemănător obiectului se referă la aceasta ca o suprafață laterală. Pe scurt, zona care ne este vizibilă se numește suprafață laterală. De exemplu, luați în considerare cilindrul așa cum se arată în figura de mai jos.
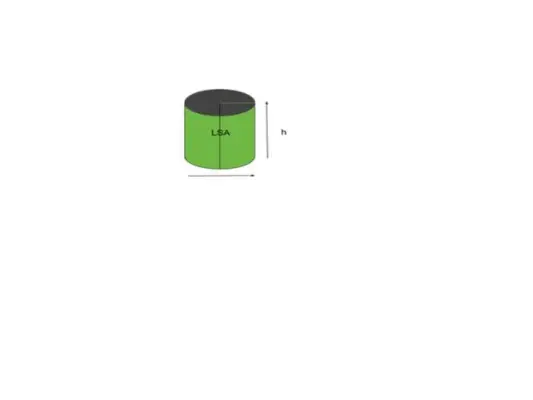
Volum
Volumul este cantitatea de spațiu dintr-un anumit obiect 3D. Cantitatea totală de spațiu pe care o ocupă un obiect sau o substanță se numește volum. Se măsoară în unități cubice.
Formule de suprafață și volum
Tabelul dat conține suprafața totală, suprafața curbată/suprafața laterală și volumul diferitelor forme.
| Numele formei | Suprafata curbata | Suprafața totală | Volum |
|---|---|---|---|
| Cuboid | 2h(l + b) | 2(lb + bh + hl) | l * b * h |
| cub | 4a2 | 6a2 | A3 |
| Cilindru | 2πrh | 2π(r + h) | πr2h |
| Sferă | 4πr2 operator java | 4πr2 | 4/3π r3 |
| Con | πrl | πr(r + l) | 1/3π r2h |
| Emisferă | 2pr2 | 3πr2 | 2/3π r3 |
Citeşte mai mult:
- Suprafața piramidei
- Suprafața cilindrului
- Suprafața emisferei
- Suprafața sferei
- Suprafața cuboidului
Exemple privind suprafețele și volumele
Exemplul 1: 2 cuburi fiecare cu un volum de 512 cm 3 sunt unite cap la cap. Aflați aria suprafeței cuboidului rezultat?
Soluţie:
Dat,
Volumul (V) al fiecărui cub este = 512 cm3
acum putem sugera că a3= 512 cm3
∴ Latura cubului, adică a = 8 cm
Acum, lățimea și lungimea cuboidului rezultat va fi de 8 cm fiecare, în timp ce înălțimea sa va fi de 16 cm.
Deci, aria suprafeței cuboidului (TSA) = 2(lb + bh + lh)
Acum, punând valorile, obținem,
= 2(8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Prin urmare, TSA al cuboidului = 640 cm 2
Exemplul 2: Avem o lumânare cilindrică, cu diametrul de 14 cm și cu lungimea de 2 cm. Se topește pentru a forma o lumânare cuboidă cu dimensiunile 7 cm × 11 cm × 1 cm. Câte lumânări cuboidale pot fi obținute?
Soluţie:
Dimensiunile lumânării cilindrice:
Raza lumânării cilindrice = 14/2 cm = 7 cm
Inaltime/grosime=2 cm
Volumul unei lumânări cilindrice = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Volumul cuboidului lumanare = 7 x 11 x 1 = 77 cm3
Prin urmare, numărul de lumânări cuboidale = Volumul lumânării cuboidale/Volumul unei lumânări cilindrice = 308/77 = 4
Prin urmare, putem obține 4 lumânări în formă de Cuboid.
Exemplul 3: O femeie dorește să construiască o minge de jucărie sferică din lut a cărei rază este egală cu raza brățărului pe care o poartă. Având în vedere că brățarul are formă circulară, ea dorește, de asemenea, ca aria brățărului să fie egală cu volumul sferei. Aflați raza brățării pe care o poartă?
Soluţie:
Fie r raza brățării, precum și sfera,
Ni s-a dat că volumul sferei este egal cu aria brățării:
Prin urmare,
πr2= 4/3 πr3
⇒ r = 3/4
Prin urmare, raza brățării este de 3/4 de unități.
Exemplul 4: Se dă că înălțimea înclinată a unui con circular drept este de 25 cm și înălțimea lui este de 24 cm. Găsiți suprafața curbată a conului?
Soluţie:
Formula pentru suprafața curbată a conului este πrl. Unde r este raza conului și l este înălțimea înclinată a conului.
Aici conul este conul circular drept.
Deci raza conului ar fi:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Acum calculând suprafața curbată sunt:
Suprafața necesară = (22/7) * 7 * 25 = 550 cm2
Prin urmare, suprafața curbată a conului este de 550 cm 2 .
Exemplul 5: Aflați aria suprafeței laterale a unui cilindru cu o rază de bază de 6 inci și o înălțime de 14 inci.
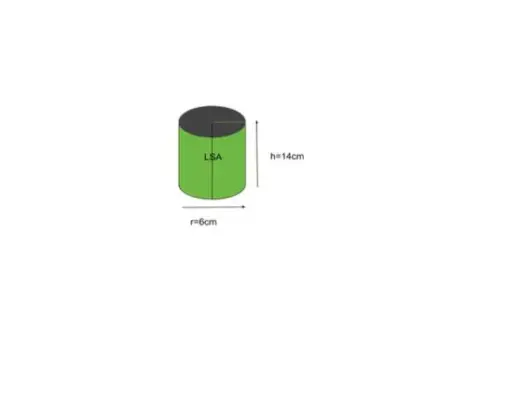
Soluţie:
Având în vedere raza r = 6, înălțimea h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527.787
= 528.
LSA a cilindrului dat este de 528 cm .
textul îngroșat în css
Întrebare de practică privind suprafețele și volumele
Variat Întrebări practice privind suprafețele și volumul formulele sunt:
Î1. Aflați aria suprafeței unui cub cu lungimea laturii de 5 centimetri.
Q2. Calculați volumul unei sfere cu raza de 3 metri.
Q3. Determinați suprafața totală a unui cilindru cu raza de 4 centimetri și înălțimea de 8 centimetri.
Î4. Aflați volumul unui con cu raza de 6 inci și înălțimea de 10 inci.
Î5. Calculați aria suprafeței unei prisme dreptunghiulare cu lungimea de 7 metri, lățime de 4 metri și înălțimea de 6 metri.
Întrebări frecvente despre formulele de suprafață și volum
Care sunt formulele pentru suprafața și volumul?
În articolul de mai sus sunt adăugate diverse formule de suprafață și volum.
Care este formula pentru volumul suprafeței clasa 10?
Formula pentru suprafața și clasa de volum 10 conține:
| Numele formei | Suprafata curbata | Suprafața totală | Volum |
|---|---|---|---|
| Cuboid factorial în c | 2h(l + b) | 2(lb + bh + hl) | l × b × h |
| cub | 4a2 | 6a2 | A3 |
| Cilindru | 2πrh | 2π(r + h) | πr2h |
| Sferă | 4πr2 | 4πr2 | 4/3π r3 |
| Con | πrl | πr(r + l) | 1/3π r2h |
| Emisferă | 2pr2 | 3πr2 | 2/3π r3 |
Care este formula cuboidului ca suprafață și volum?
- Aria suprafeței cuboidului = 2(lb + bh + hl)
- Volumul lui Cubiod = l × b × h
Care este suprafața și volumul?
Suprafața este aria tuturor suprafețelor unui solid, iar volumul acestuia este spațiul ocupat de sloid.
