O funcție recursivă poate fi definită ca o rutină care se autoinvocă direct sau indirect.

Cu alte cuvinte, o funcție recursivă este o funcție care rezolvă o problemă prin rezolvarea unor instanțe mai mici ale aceleiași probleme. Această tehnică este folosită în mod obișnuit în programare pentru a rezolva probleme care pot fi împărțite în subprobleme mai simple, similare.

Nevoia funcției recursive:

O funcție recursivă este o funcție care rezolvă o problemă prin rezolvarea unor instanțe mai mici ale aceleiași probleme. Această tehnică este adesea folosită în programare pentru a rezolva probleme care pot fi împărțite în subprobleme mai simple, similare.

1. Rezolvarea sarcinilor complexe:

Funcțiile recursive împart problemele complexe în instanțe mai mici ale aceleiași probleme, rezultând un cod compact și ușor de citit.

2. Împărțiți și cuceriți:

Funcțiile recursive sunt potrivite pentru algoritmii de împărțire și cucerire, cum ar fi sortarea prin îmbinare și sortarea rapidă, împărțirea problemelor în subprobleme mai mici, rezolvarea acestora recursiv și îmbinarea soluțiilor cu problema originală.

3. Întoarcerea înapoi :

Backtracking recursiv este ideal pentru explorarea și rezolvarea problemelor precum N-Queens și Sudoku.

cadru de colecție java

4. Dinamic programare:

Funcțiile recursive rezolvă eficient problemele de programare dinamică prin rezolvarea subproblemelor și combinând soluțiile acestora într-o soluție completă.

5. Arborele și structuri grafice:

Funcțiile recursive sunt excelente pentru lucrul cu structuri arborescente și grafice, simplificând sarcinile de traversare și de recunoaștere a modelelor .

Cum se scrie o functie recursiva:

Componentele unei funcții recursive:

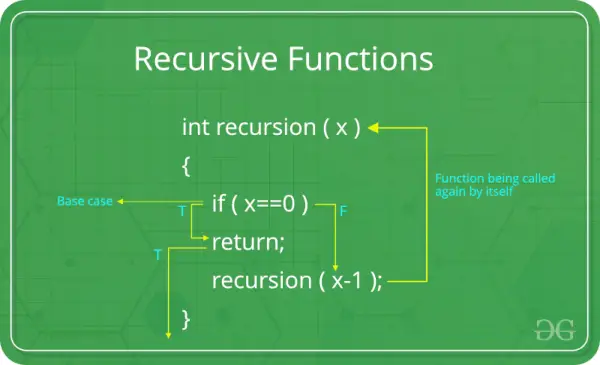
Caz de baza: Fiecare funcție recursivă trebuie să aibă un caz de bază. Cazul de bază este cel mai simplu scenariu care nu necesită recursivitate suplimentară. Aceasta este o condiție de terminare care împiedică funcția să se autoapeleze pe termen nelimitat. Fără un caz de bază adecvat, o funcție recursivă poate duce la recursivitate infinită.

Caz recursiv: În cazul recursiv, funcția se autoapelează cu argumentele modificate. Aceasta este esența recursiunii – rezolvarea unei probleme mai mari prin împărțirea ei în cazuri mai mici ale aceleiași probleme. Cazul recursiv ar trebui să se apropie de cazul de bază cu fiecare iterație.

Să luăm în considerare exemplul lui factorial de număr :

ce este obj în java

În acest exemplu, cazul de bază este când n este 0 , iar funcția revine 1 . Cazul recursiv se înmulțește n cu rezultatul funcției apelate cu parametru n – 1 . Procesul continuă până când se ajunge la cazul de bază.

Este esențial să vă asigurați că funcția recursivă are un caz de bază corect și că apelurile recursive duc la cazul de bază, în caz contrar, procedura s-ar putea rula pe termen nelimitat, ducând la o depășire a stivei (depășind memoria disponibilă alocată apelurilor de funcții).

Mai jos este implementarea factorialului unui număr:

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Complexitatea timpului: Pe)
Spațiu auxiliar: Pe)