Graficul cuantile-quantile ( diagrama q-q) este o metodă grafică pentru a determina dacă un set de date urmează o anumită distribuție de probabilitate sau dacă două mostre de date provin din aceeași populatie sau nu. Diagramele Q-Q sunt deosebit de utile pentru a evalua dacă un set de date este distribuite normal sau dacă urmează vreo altă distribuţie cunoscută. Ele sunt utilizate în mod obișnuit în statistici, analiza datelor și controlul calității pentru a verifica ipotezele și a identifica abaterile de la distribuțiile așteptate.
Quantile și percentile
Quantilele sunt puncte dintr-un set de date care împart datele în intervale care conțin probabilități sau proporții egale ale distribuției totale. Ele sunt adesea folosite pentru a descrie răspândirea sau distribuția unui set de date. Cele mai comune cuantile sunt:
- Median (percentila 50) : mediana este valoarea medie a unui set de date atunci când este ordonat de la cel mai mic la cel mai mare. Împarte setul de date în două jumătăți egale.
- Quartiles (25, 50 și 75 percentile) : Quartilele împart setul de date în patru părți egale. Prima cuartilă (Q1) este valoarea sub care se încadrează 25% din date, a doua cuartilă (Q2) este mediana, iar a treia cuartilă (Q3) este valoarea sub care se încadrează 75% din date.
- Percentile : Percentilele sunt similare cu quartilele, dar se împarte setul de date în 100 de părți egale. De exemplu, a 90-a percentila este valoarea sub care se încadrează 90% din date.
Notă:
- Un grafic q-q este un grafic al cuantilelor primului set de date în raport cu cuantilele celui de-al doilea set de date.
- În scopuri de referință, este trasată și o linie de 45%; Pentru dacă eșantioanele provin din aceeași populație, atunci punctele sunt de-a lungul acestei linii.
Distributie normala:
Distribuția normală (alias curba Bell de distribuție Gaussiană) este o distribuție continuă de probabilitate reprezentând distribuția obținută din valorile reale generate aleatoriu.
. 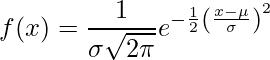

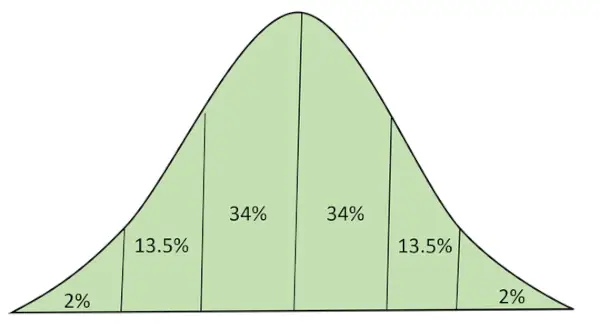
Distribuție normală cu zonă sub curbă
Cum se desenează diagrama Q-Q?
Pentru a desena o diagramă cuantil-cantil (Q-Q), puteți urma acești pași:
- Colectați Datele : Adunați setul de date pentru care doriți să creați diagrama Q-Q. Asigurați-vă că datele sunt numerice și reprezintă un eșantion aleatoriu din populația de interes.
- Sortați datele : Aranjați datele în ordine crescătoare sau descrescătoare. Acest pas este esențial pentru calcularea cuantilelor cu precizie.
- Alegeți o distribuție teoretică : Determinați distribuția teoretică cu care doriți să comparați setul de date. Opțiunile comune includ distribuția normală, distribuția exponențială sau orice altă distribuție care se potrivește bine datelor dvs.
- Calculați cuantile teoretice : Calculați cuantilele pentru distribuția teoretică aleasă. De exemplu, dacă comparați cu o distribuție normală, veți folosi funcția de distribuție cumulativă inversă (CDF) a distribuției normale pentru a găsi cuantilele așteptate.
- Complot :
- Trasează valorile setului de date sortate pe axa x.
- Trasează cuantilele teoretice corespunzătoare pe axa y.
- Fiecare punct de date (x, y) reprezintă o pereche de valori observate și așteptate.
- Conectați punctele de date pentru a inspecta vizual relația dintre setul de date și distribuția teoretică.
Interpretarea diagramei Q-Q
- Dacă punctele de pe diagramă cad aproximativ de-a lungul unei linii drepte, sugerează că setul de date urmează distribuția presupusă.
- Abaterile de la linia dreaptă indică abateri de la distribuția presupusă, necesitând investigații suplimentare.
Explorarea asemănării distribuției cu diagramele Q-Q
Explorarea similarității distribuției folosind diagrame Q-Q este o sarcină fundamentală în statistică. Compararea a două seturi de date pentru a determina dacă provin din aceeași distribuție este vitală pentru diverse scopuri analitice. Atunci când ipoteza unei distribuții comune este valabilă, îmbinarea seturilor de date poate îmbunătăți acuratețea estimării parametrilor, cum ar fi locația și scara. Diagramele Q-Q, prescurtare pentru diagramele cuantile-cuantile, oferă o metodă vizuală pentru evaluarea similitudinii distribuției. În aceste grafice, cuantilele dintr-un set de date sunt reprezentate în raport cu cuantilele din altul. Dacă punctele se aliniază strâns de-a lungul unei linii diagonale, aceasta sugerează similitudini între distribuții. Abaterile de la această linie diagonală indică diferențe în caracteristicile de distribuție.
În timp ce teste ca chi-pătrat și Kolmogorov-Smirnov testele pot evalua diferențele generale de distribuție, diagramele Q-Q oferă o perspectivă nuanțată prin compararea directă a cuantilelor. Acest lucru le permite analiștilor să discearnă diferențe specifice, cum ar fi schimbări de locație sau schimbări de scară, care ar putea să nu fie evidente doar din testele statistice formale.
Implementarea Python a diagramei Q-Q
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Ieșire:
complot Q-Q
Aici, deoarece punctele de date urmează aproximativ o linie dreaptă în diagrama Q-Q, sugerează că setul de date este în concordanță cu distribuția teoretică asumată, care în acest caz am presupus că este distribuția normală.
Avantajele diagramei Q-Q
- Comparație flexibilă : diagramele Q-Q pot compara seturi de date de diferite dimensiuni fără care necesită dimensiuni egale ale eșantionului.
- Analiză fără dimensiuni : sunt fără dimensiuni, ceea ce le face potrivite pentru compararea seturi de date cu diferite unități sau scale.
- Interpretare vizuală : Oferă o reprezentare vizuală clară a distribuției datelor în comparație cu o distribuție teoretică.
- Sensibilă la abateri : detectează cu ușurință abaterile de la distribuțiile presupuse, ajutând la identificarea discrepanțelor de date.
- Instrument de diagnosticare : Ajută la evaluarea ipotezelor de distribuție, la identificarea valorii aberante și la înțelegerea tiparelor de date.
Aplicații ale diagramei cuantile-cantile
Diagrama cuantil-cantil este utilizat în următorul scop:
- Evaluarea ipotezelor distribuționale : Diagramele Q-Q sunt frecvent utilizate pentru a inspecta vizual dacă un set de date urmează o distribuție de probabilitate specifică, cum ar fi distribuția normală. Prin compararea cuantilelor datelor observate cu cuantilele distribuției presupuse, pot fi detectate abateri de la distribuția presupusă. Acest lucru este crucial în multe analize statistice, unde validitatea ipotezelor distribuționale influențează acuratețea inferențelor statistice.
- Detectarea Outliers : valorile aberante sunt puncte de date care se abate semnificativ de la restul setului de date. Diagramele Q-Q pot ajuta la identificarea valorii aberante prin dezvăluirea punctelor de date care sunt departe de modelul așteptat al distribuției. Valorile aberante pot apărea ca puncte care se abat de la linia dreaptă așteptată în grafic.
- Compararea distribuțiilor : diagramele Q-Q pot fi folosite pentru a compara două seturi de date pentru a vedea dacă provin din aceeași distribuție. Acest lucru se realizează prin trasarea cuantilelor unui set de date în raport cu cuantilele altui set de date. Dacă punctele cad aproximativ de-a lungul unei linii drepte, sugerează că cele două seturi de date sunt extrase din aceeași distribuție.
- Evaluarea normalității : diagramele Q-Q sunt deosebit de utile pentru evaluarea normalității unui set de date. Dacă punctele de date din diagramă urmează îndeaproape o linie dreaptă, aceasta indică faptul că setul de date este distribuit aproximativ normal. Abaterile de la linie sugerează abateri de la normalitate, ceea ce poate necesita investigații suplimentare sau tehnici statistice neparametrice.
- Validarea modelului : În domenii precum econometria și învățarea automată, diagramele Q-Q sunt folosite pentru a valida modelele predictive. Prin compararea cuantilelor răspunsurilor observate cu cuantilele prezise de un model, se poate evalua cât de bine modelul se potrivește datelor. Abaterile de la modelul așteptat pot indica domenii în care modelul necesită îmbunătățiri.
- Control de calitate : Diagramele Q-Q sunt folosite în procesele de control al calității pentru a monitoriza distribuția valorilor măsurate sau observate în timp sau în diferite loturi. Abaterile de la modelele așteptate din complot pot semnala schimbări în procesele de bază, determinând investigații suplimentare.
Tipuri de diagrame Q-Q
Există mai multe tipuri de diagrame Q-Q utilizate în mod obișnuit în statistici și analize de date, fiecare potrivit pentru diferite scenarii sau scopuri:
- Distributie normala : O distribuție simetrică în care diagrama Q-Q ar arăta puncte aproximativ de-a lungul unei linii diagonale dacă datele aderă la o distribuție normală.
- Distribuție înclinată la dreapta : O distribuție în care diagrama Q-Q ar afișa un model în care cuantilele observate deviază de la linia dreaptă spre capătul superior, indicând o coadă mai lungă pe partea dreaptă.
- Distribuție declinată la stânga : O distribuție în care diagrama Q-Q ar prezenta un model în care cuantilele observate deviază de la linia dreaptă spre capătul inferior, indicând o coadă mai lungă pe partea stângă.
- Distribuție sub-dispersată : O distribuție în care diagrama Q-Q ar arăta cuantile observate grupate mai strâns în jurul liniei diagonale în comparație cu cuantilele teoretice, sugerând o variație mai mică.
- Distribuție supradispersată : O distribuție în care diagrama Q-Q ar afișa cuantile observate mai răspândite sau care se abate de la linia diagonală, indicând o varianță sau o dispersie mai mare în comparație cu distribuția teoretică.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>>>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Ieșire:
Diagrama Q-Q pentru diferite distribuții
pd.merge
