Forța normală este definită ca forța exercitată de orice suprafață asupra altui obiect. Când un obiect este în repaus, forța netă exercitată asupra acestuia este egală cu zero. O forță normală nu poate fi aplicată pe două suprafețe care nu sunt conectate una cu cealaltă. Poate fi interpretat ca o componentă a forței care este verticală pe orice suprafață de contact. Determină cât de multă forță eliberează corpul la sol. Forța normală este egală cu greutatea obiectului numai dacă rata de schimbare a vitezei obiectului este negativă, ceea ce înseamnă că acesta decelerează.
Formulă
Valoarea forței normale depinde de locul în care este plasat obiectul față de celălalt obiect. Când un obiect urmează să cadă, poziția în care obiectul cade pe pământ determină valoarea forței normale. Forța normală este notă cu simbolul FN. Unitatea sa de măsură este Newtoni (N) iar formula dimensională este dată de [M1L1T-2].
Dacă un corp se sprijină pe o forță plană, forța normală este egală cu valoarea greutății gravitaționale, adică mg.
F N = mg
Unde,
FNeste forța normală,
m este masa obiectului în repaus,
g este accelerația datorată gravitației.
Dacă un corp alunecă în jos de pe o suprafață înclinată la un anumit unghi, valoarea forței normale este greutatea gravitațională adăugată de o forță suplimentară de F sin θ. În acest caz, forța normală este mai mare decât greutatea obiectului.
F N = mg + F sin θ
Unde,
FNeste forța normală,
m este masa obiectului alunecat,
g este accelerația datorată gravitației,
θ este unghiul de înclinare.
Dacă forța acționează asupra unui corp în direcție ascendentă, valoarea forței normale este greutatea gravitațională decrementată de o forță F sin θ. În acest caz, forța normală netă este mai mică decât greutatea obiectului.
F N = mg – F sin θ
Unde,
Comandă rapidă cu majuscule excelFNeste forța normală,
m este masa obiectului alunecat,
g este accelerația datorată gravitației,
θ este unghiul de înclinare.
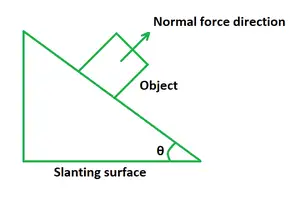
Dacă un corp este plasat pe un plan înclinat, forța normală FNeste egal cu produsul dintre greutatea gravitațională și cosinusul unghiului de înclinare.
F N = mg cos θ
Unde,
FNeste forța normală,
m este masa obiectului alunecat,
g este accelerația datorată gravitației,
θ este unghiul de înclinare.
Exemple de probleme
Problema 1. Un obiect cu masa de 2 kg se sprijină pe o masă. Calculați forța normală exercitată asupra acestuia.
Soluţie:
Avem,
m = 2
g = 9,8
Folosind formula pe care o obținem,
FN= mg
= 2 (9,8)
= 19,6 N
Problema 2. Un obiect se sprijină pe o masă cu o forță de 39,2 N. Calculați forța normală exercitată asupra acestuia.
Soluţie:
Avem,
F = 39,2
g = 9,8
Folosind formula pe care o obținem,
FN= mg
=> m = F/g
=> m = 39,2/9,8
=> m = 4 kg
Problema 3. Un obiect cu masa de 10 kg alunecă în jos cu o forță de 200 N de pe o suprafață înclinată la un unghi de 30°. Calculați forța normală exercitată asupra acestuia.
Soluţie:
Avem,
parseint javaF = 200
m = 10
g = 9,8
θ = 30°
Folosind formula pe care o obținem,
FN= mg + F sin θ
= 10 (9,8) + 200 sin 30°
= 98 + 200 (1/2)
= 98 + 100
= 198 N
Problema 4. Un obiect cu masa de 20 kg alunecă în jos cu o forță de 400 N de pe o suprafață înclinată la un unghi de 30°. Calculați forța normală exercitată asupra acestuia.
Soluţie:
Avem,
F = 400
m = 20
g = 9,8
θ = 30°
Folosind formula pe care o obținem,
FN= mg + F sin θ
= 20 (9,8) + 400 fără 30°
= 196 + 400 (1/2)
= 196 + 200
= 396 N
sort array java
Problema 5. Un obiect cu o masă de 15 kg este plasat pe o suprafață înclinată la un unghi de 30°. Calculați forța normală exercitată asupra acesteia dacă forța acționează în sus cu o valoare de 100 N.
Soluţie:
Avem,
F = 100
m = 15
g = 9,8
θ = 30°
Folosind formula pe care o obținem,
FN= mg – F sin θ
= 15 (9,8) – 100 fără 30°
= 147 – 100 (1/2)
= 147 – 50
= 97 N
Problema 6. Un obiect cu masa de 5 kg este plasat pe o suprafață înclinată la un unghi de 60°. Calculați forța normală exercitată asupra acestuia în orice punct.
Soluţie:
Avem,
m = 5
g = 9,8
θ = 60°
Folosind formula pe care o obținem,
FN= mg cos θ
= 5 (9,8) (cos 60°)
= 49/2
= 24,5 N
Problema 7. Un obiect este plasat pe o suprafață înclinată la un unghi de 60°. Calculați-i masa dacă forța normală exercitată asupra sa este de 400 N.
Soluţie:
Avem,
FN= 400,
θ = 60°
Folosind formula pe care o obținem,
FN= mg cos θ
m = F/(g cos θ)
= 400/ (9,8 × cos 60°)
= 400/4,9
= 81,63 N
