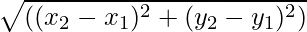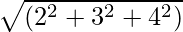logo

TechCodeview

Mărimea unui vector

Mărimile vectoriale sunt mărimile care au atât direcție, cât și mărime. Mărimea unui vector este lungimea vectorului. Este dat de valoarea numerică a vectorului și, deoarece reprezintă lungimea vectorului, este întotdeauna pozitiv. Pentru orice vector 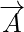overrightarrow{A}amploarea sa este reprezentată ca overrightarrow{A}.

Să aflăm mai multe despre mărimea vectorului cu formula sa, exemple și altele în acest articol.



Cuprins

Care este mărimea unui vector?

Mărimea unui vector este definită ca lungimea vectorului. Deoarece mărimea vectorului indică lungimea vectorului, acesta este întotdeauna pozitiv. Pentru orice vector A mărimea lui este reprezentată ca |A|. Să presupunem că un vector este definit ca xi + yj, atunci mărimea lui este definită ca rădăcina pătrată a sumei pătratelor termenilor individuali. Mărimea vectorului reprezintă lungimea vectorului, adică valoarea sau impactul pe care îl are vectorul.

De exemplu, dacă o forță de 5i N lucrează asupra unui obiect, atunci mărimea sa este de 5 N, ceea ce înseamnă că puterea forței aplicate este de 5 N și „ eu’ în 5i reprezintă că se aplică în direcția x pozitivă.



Mărimea unei formule vectoriale

Există diferite moduri de a calcula mărimea vectorului. Pe baza datelor date, utilizați un alt tip de formulă pentru a găsi mărimea unui vector. Mărimea unui vector A este reprezentată folosind operatorul modul, adică |A|

Există diverse formule care sunt folosite pentru a număra mărimea vectorului. Următoarea imagine arată formulele importante utilizate pentru a găsi mărimea vectorului.

Mărimea unei formule vectoriale

Următoarele sunt modalitățile de calculare a mărimii.



  • Dacă li se dă un vector Ā = xi+ yĵ + zk̂, atunci mărimea vectorului Ā poate fi calculată folosind formula de mai jos

Mărimea vectorului Ā (|A|) = √(x 2 + și 2 +z 2 )

  • Dacă vectorul punct de plecare este să spunem (x1, și1) și punctul final al unui vector este să spunem (x2, și2) sunt date atunci mărimea vectorului overrightarrow{AB}este dat de,
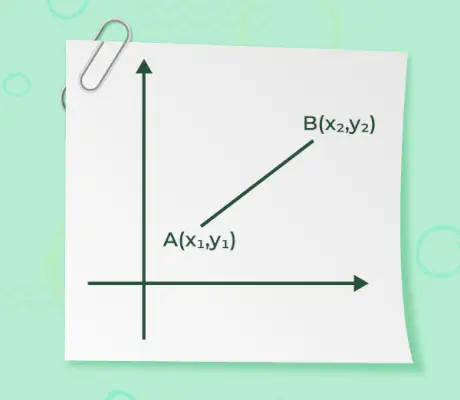
Mărimea Vectorului dacă sunt date două puncte

Mărimea unui vector, când sunt date punctele de început și de sfârșit ale unui vector, nu este altceva decât distanța dintre puncte. Formula pentru găsirea mărimii este dată de

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Dacă oricare dintre punctele de început sau de capăt ale unui vector se află la originea o(0, 0) și un alt punct este A(x, y) așa cum este specificat în figura de mai jos,
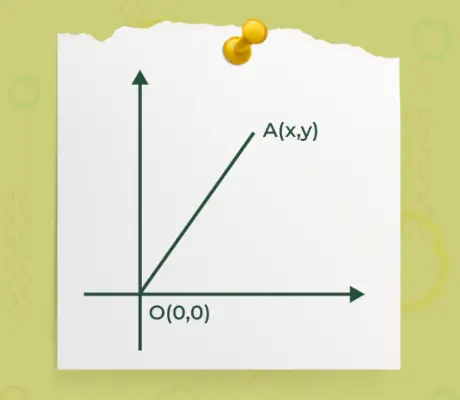
Mărimea Vectorului dacă este dat un punct și o origine

Atunci formula pentru găsirea mărimii unui vector unde unul dintre capetele unui vector este la origine este dată de

|Â| = √(x 2 +y 2 )

Direcția unui vector

Mărimile vectoriale sunt mărimi care au atât mărimi, cât și direcții. Direcția mărimii vectoriale indică în ce direcție este aplicată mărimea vectorială. Este definit ca unghiul pe care vectorul îl formează cu linia orizontală sau cu axa x. Este reprezentat prin simbol A .

Imaginea de mai jos arată săgeata care este folosită pentru a arăta direcția vectorului.

Direcția Vectorului

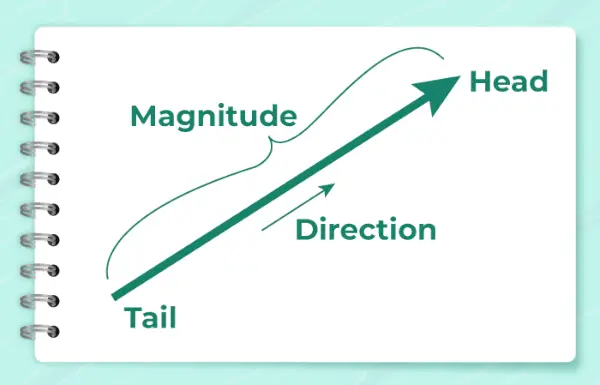
Se calculează folosind formula,

α = bronz -1 (y/x)

throw throws în java

Pentru vectorul generat de coordonatele (x1, și1) și (x2, și2) direcția lor este dată de formula,

α = bronz -1 [(și 2 - și 1 )/(X 2 - X 1 )]

Cum să găsiți mărimea unui vector?

Mărimea vectorului este calculată utilizând pașii discutați mai jos,

Pasul 1: Identificați componentele x, y și z ale vectorului.

Pasul 2 : Aflați pătratul tuturor componentelor x, y și z.

Pasul 3: Adăugați toate pătratele găsite la pasul 2.

Pasul 4: Găsiți rădăcina pătrată a sumei obținute la pasul 3.

exemplu de listă în java

Valoarea obținută după pasul 4 este mărimea vectorului dat.

Exemplu: Aflați mărimea vectorului A = 3i + 4j

Soluţie:

Mărimea vectorului A este calculată utilizând pașii discutați mai sus.

Pasul 1: Comparând A = 3i + 4j cu xi + yj obținem x = 3 și y = 4

Pasul 2: X2= 32= 9 și y2= 42= 16

Pasul 3: X2+ și2= 9 + 16 = 25

Pasul 4: √(25) = 5

Astfel, mărimea vectorului A = 3i + 4j este de 5 unități.

Concluzie

În concluzie, mărimea unui vector ne spune cât de lung este vectorul. Acest concept este foarte important în multe domenii precum fizica, inginerie și informatică, deoarece ajută la măsurarea lucrurilor precum viteza, forța și direcția mișcării. Înțelegând magnitudinea vectorului, putem analiza și rezolva mai bine problemele practice, făcându-l o cunoaștere cheie pentru oricine lucrează cu numere și măsurători în aplicații din lumea reală.

Citeşte mai mult,

Exemple rezolvate despre mărimea vectorului

Exemplul 1: Aflați mărimea vectorului  = 2i + 3ĵ + 4k.

Soluţie:

pregătiți-vă pentru testul mockito

Dat,

 = 2i + 3ĵ + 4k

Magnitudine |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Mărimea vectorului 2i+3ĵ+4k este 5.38 unitate

Exemplul 2: Aflați mărimea vectorului  = 3i + 3ĵ – 6k

Soluţie:

Dat

 = 3i + 3ĵ – 6k

Magnitudine |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Mărimea vectorului 3i+ 3ĵ – 6k este 7.35 unitate.

Exemplul 3: Găsiți mărimea vectorului dacă punctul de pornire al unui vector este (3, 4) și punctul final este (6, 2).

Soluţie:

Dat,

(X1, și1) = (3, 4)
(X2, și2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Astfel, mărimea vectorului dat este 3.6 unitate.

Exemplul 4: Aflați mărimea vectorului dacă punctul de pornire al unui vector este (2, 1, 4) și punctul final este (5, 2, 6).

Soluţie:

Dat,

(X1, și1, Cu1) = (2, 1, 4)

(X2, și2, Cu2) = (5, 2, 6)

|Â| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Astfel, mărimea vectorului dat este 3,74 unitate.

Exemplul 5: Care este mărimea vectorului care începe la origine și punctul final la (3, 4).

Soluţie:

panda iterrows

Dat,

Punctul de pornire al vectorului este O(0, 0)

Punct final (x, y) = (3, 4)

Mărimea vectorului (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Astfel, mărimea vectorului dat este 5 unitate.

Exemplul 6: Găsiți mărimea vectorului în care unul dintre punctele de capăt este la origine și celălalt punct la (1, 4, 3).

Soluţie:

Dat,

Punctul final al vectorului este O(0, 0)

Alt punct (x, y, z) = (1, 4, 3)

Mărimea vectorului (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Astfel, mărimea vectorului dat este 5.09 unitate.

algoritm de sortare rapidă

Întrebări frecvente despre mărimea unui vector

Care este mărimea unei formule vectoriale?

Mărimea unui vector este valoarea numerică a vectorului și definește lungimea vectorului. Pentru orice vector, A mărimea sa este reprezentată ca |A|. Mărimea vectorului este calculată folosind formula,

Pentru orice vector, A = xi + yj + zk mărimea lui este dată de formula

|A| = √(x 2 + și 2 + z 2 )

Pentru orice vector al cărui punct de început și, respectiv, punctul final sunt (x1, și1) și (x2, și2) mărimea sa este dată de formula

|A| = √((x 2 - X 1 ) 2 + (și 2 - și 1 ) 2 )

Cum se reprezintă mărimea unui vector?

Mărimea vectorului A este reprezentată prin simbolul |A|.

Cum să găsiți mărimea unui vector?

Sunt folosite diverse formule pentru a calcula mărimea vectorului, unele dintre ele sunt,

  • |A| = √(x 2 + și 2 + z 2 ) când vectorul este sub forma A = xi + yj + zk
  • |A| = √((x) 2 + (și) 2 ) când vectorul este dat de punctul A (x, y) și originea O(0, 0).
  • |A| = √((x 2 - X 1 ) 2 + (și 2 - și 1 ) 2 ) când vectorul este dat de punctul A (x1, și2) și punctul B (x2, și2).

Găsiți un vector cu magnitudinea 5.

Există diferiți vectori care pot avea o magnitudine de 5, un exemplu din care este vectorul A reprezentat ca,

A = 3i + 4j Sau A = 4i + 5j