Algoritmul Luhn, cunoscut și sub numele de modulul 10 sau spre 10 algoritm, este o formulă simplă de sumă de control utilizată pentru a valida o varietate de numere de identificare, cum ar fi numere de card de credit, numere IMEI, numere de asigurări sociale canadiene. Formula LUHN a fost creată la sfârșitul anilor 1960 de un grup de matematicieni. La scurt timp după aceea, companiile de carduri de credit l-au adoptat. Deoarece algoritmul este în domeniul public, poate fi folosit de oricine. Majoritatea cardurilor de credit și multe numere de identificare guvernamentale folosesc algoritmul ca o metodă simplă de a distinge numerele valide de numerele greșite sau incorecte. A fost conceput pentru a proteja împotriva erorilor accidentale, nu a atacurilor rău intenționate.
Pași implicați în algoritmul Luhn
Să înțelegem algoritmul cu un exemplu:
Luați în considerare exemplul unui număr de cont 79927398713 .
Pasul 1 – Pornind de la cea mai dreaptă cifră, dublați valoarea fiecărei a doua cifre,
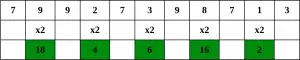
Pasul 2 – Dacă dublarea unui număr are ca rezultat un număr cu două cifre, adică mai mare decât 9 (de exemplu, 6 × 2 = 12), atunci adăugați cifrele produsului (de exemplu, 12: 1 + 2 = 3, 15: 1 + 5 = 6), pentru a obține un număr cu o singură cifră.

Pasul 3 – Acum luați suma tuturor cifrelor.
algoritmul knn

Pasul 4 – Dacă totalul modulo 10 este egal cu 0 (dacă totalul se termină cu zero), atunci numărul este valabil conform formulei Luhn; altfel nu este valabil.

Deoarece suma este 70, care este un multiplu al lui 10, numărul contului este posibil să fie valid.
Ideea este simplă; traversăm de la capăt. Pentru fiecare a doua cifră, o dublem înainte de a o adăuga. Adăugăm două cifre ale numărului obținut după dublare.
Implementare:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
subșir de metodă java
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
exemplu de nume de utilizator
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)>>> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
0,0625 sub formă de fracție
>Ieșire
This is a valid card>
Algoritmul Luhn detectează orice eroare cu o singură cifră, precum și aproape toate transpozițiile cifrelor adiacente.
