Având în vedere două șiruri „X” și „Y”, găsiți lungimea celui mai lung subșir comun.
Exemple:
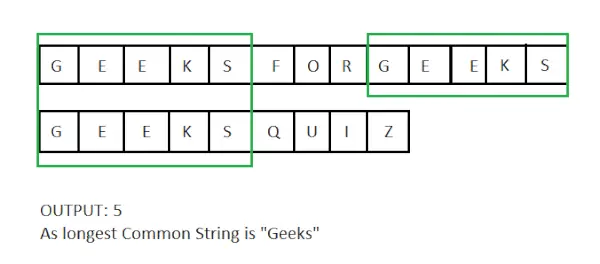
Intrare : X = techcodeview.com, y = GeeksQuiz
Ieșire : 5
Explicaţie:
Cel mai lung subșir comun este Geeks și are lungimea de 5.
Intrare : X = abcdxyz, y = xyzabcd
Ieșire: 4
Explicaţie:
Cel mai lung subșir comun este abcd și are lungimea 4.Intrare : X = zxabcdezy, y = yzabcdezx
Ieșire: 6
Explicaţie:
Cel mai lung subșir comun este abcdez și are lungimea 6.
Abordare:
Fie m și n lungimile primului și, respectiv, celui de-al doilea șir.
A solutie simpla este de a lua în considerare unul câte unul toate subșirurile primului șir și pentru fiecare subșir verificați dacă este un subșir din al doilea șir. Urmăriți subșirul de lungime maximă. Vor exista subșiruri O(m^2) și putem afla dacă un șir este subșir pe alt șir în timpul O(n) (vezi acest ). Deci, complexitatea de timp generală a acestei metode ar fi O(n * m2)
Programare dinamică poate fi folosit pentru a găsi cel mai lung subșir comun în timp O(m*n). Ideea este să găsiți lungimea celui mai lung sufix comun pentru toate subșirurile ambelor șiruri și să stocați aceste lungimi într-un tabel.
Cel mai lung sufix comun are următoarea proprietate optimă a substructurii.
Dacă ultimele caractere se potrivesc, atunci reducem ambele lungimi cu 1
- LCSuff(X, Y, m, n) = LCSuff(X, Y, m-1, n-1) + 1 dacă X[m-1] = Y[n-1]
Dacă ultimele caractere nu se potrivesc, atunci rezultatul este 0, adică
- LCSuff(X, Y, m, n) = 0 dacă (X[m-1] != Y[n-1])
Acum luăm în considerare sufixele diferitelor subșiruri care se termină la indici diferiți.
Lungimea maximă Cel mai lung sufix comun este cel mai lung subșir comun.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)) unde 1 <= i <= m și 1 <= j <= n
În continuare este implementarea iterativă a soluției de mai sus.
C++
/* Dynamic Programming solution to> >find length of the> >longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> >common substring of X[0..m-1]> >and Y[0..n-1] */> int> LCSubStr(>char>* X,>char>* Y,>int> m,>int> n)> {> >// Create a table to store> >// lengths of longest> >// common suffixes of substrings.> >// Note that LCSuff[i][j] contains> >// length of longest common suffix> >// of X[0..i-1] and Y[0..j-1].> >int> LCSuff[m + 1][n + 1];> >int> result = 0;>// To store length of the> >// longest common substring> >/* Following steps build LCSuff[m+1][n+1] in> >bottom up fashion. */> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >// The first row and first column> >// entries have no logical meaning,> >// they are used only for simplicity> >// of program> >if> (i == 0 || j == 0)> >LCSuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> >result = max(result, LCSuff[i][j]);> >}> >else> >LCSuff[i][j] = 0;> >}> >}> >return> result;> }> // Driver code> int> main()> {> >char> X[] =>'OldSite:techcodeview.com.org'>;> >char> Y[] =>'NewSite:GeeksQuiz.com'>;> >int> m =>strlen>(X);> >int> n =>strlen>(Y);> >cout <<>'Length of Longest Common Substring is '> ><< LCSubStr(X, Y, m, n);> >return> 0;> }> |
>
>
Java
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> >/*> >Returns length of longest common substring> >of X[0..m-1] and Y[0..n-1]> >*/> >static> int> LCSubStr(>char> X[],>char> Y[],>int> m,>int> n)> >{> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> >int> LCStuff[][] =>new> int>[m +>1>][n +>1>];> >// To store length of the longest> >// common substring> >int> result =>0>;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (>int> i =>0>; i <= m; i++) {> >for> (>int> j =>0>; j <= n; j++) {> >if> (i ==>0> || j ==>0>)> >LCStuff[i][j] =>0>;> >else> if> (X[i ->1>] == Y[j ->1>]) {> >LCStuff[i][j]> >= LCStuff[i ->1>][j ->1>] +>1>;> >result = Integer.max(result,> >LCStuff[i][j]);> >}> >else> >LCStuff[i][j] =>0>;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> main(String[] args)> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.length();> >int> n = Y.length();> >System.out.println(> >'Length of Longest Common Substring is '> >+ LCSubStr(X.toCharArray(), Y.toCharArray(), m,> >n));> >}> }> // This code is contributed by Sumit Ghosh> |
>
>
Python3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> ># Create a table to store lengths of> ># longest common suffixes of substrings.> ># Note that LCSuff[i][j] contains the> ># length of longest common suffix of> ># X[0...i-1] and Y[0...j-1]. The first> ># row and first column entries have no> ># logical meaning, they are used only> ># for simplicity of the program.> ># LCSuff is the table with zero> ># value initially in each cell> >LCSuff>=> [[>0> for> k>in> range>(n>+>1>)]>for> l>in> range>(m>+>1>)]> ># To store the length of> ># longest common substring> >result>=> 0> ># Following steps to build> ># LCSuff[m+1][n+1] in bottom up fashion> >for> i>in> range>(m>+> 1>):> >for> j>in> range>(n>+> 1>):> >if> (i>=>=> 0> or> j>=>=> 0>):> >LCSuff[i][j]>=> 0> >elif> (X[i>->1>]>=>=> Y[j>->1>]):> >LCSuff[i][j]>=> LCSuff[i>->1>][j>->1>]>+> 1> >result>=> max>(result, LCSuff[i][j])> >else>:> >LCSuff[i][j]>=> 0> >return> result> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> print>(>'Length of Longest Common Substring is'>,> >LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
>
>
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> >// Returns length of longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> LCSubStr(>string> X,>string> Y,>int> m,>int> n)> >{> >// Create a table to store lengths of> >// longest common suffixes of substrings.> >// Note that LCSuff[i][j] contains length> >// of longest common suffix of X[0..i-1]> >// and Y[0..j-1]. The first row and first> >// column entries have no logical meaning,> >// they are used only for simplicity of> >// program> >int>[, ] LCStuff =>new> int>[m + 1, n + 1];> >// To store length of the longest common> >// substring> >int> result = 0;> >// Following steps build LCSuff[m+1][n+1]> >// in bottom up fashion> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >if> (i == 0 || j == 0)> >LCStuff[i, j] = 0;> >else> if> (X[i - 1] == Y[j - 1])> >{> >LCStuff[i, j]> >= LCStuff[i - 1, j - 1] + 1;> >result> >= Math.Max(result, LCStuff[i, j]);> >}> >else> >LCStuff[i, j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> Main()> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >Console.Write(>'Length of Longest Common'> >+>' Substring is '> >+ LCSubStr(X, Y, m, n));> >}> }> // This code is contributed by Sam007.> |
>
>
Javascript
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> >/*> >Returns length of longest common> >substring of X[0..m-1] and Y[0..n-1]> >*/> >function> LCSubStr( X, Y , m , n) {> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> > >var> LCStuff => >Array(m + 1).fill().map(()=>Array(n + 1).fill(0));> >// To store length of the longest> >// common substring> >var> result = 0;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (i = 0; i <= m; i++) {> >for> (j = 0; j <= n; j++) {> >if> (i == 0 || j == 0)> >LCStuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> >result = Math.max(result, LCStuff[i][j]);> >}>else> >LCStuff[i][j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> > >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> >var> m = X.length;> >var> n = Y.length;> >document.write(>'Length of Longest Common Substring is '> +> >LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
>
>
PHP
lista de matrice sortată în java
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>>>> |
>Length of Longest Common Substring is 10>
Complexitatea timpului: O(m*n)
Spațiu auxiliar: O(m*n), deoarece m*n spațiu suplimentar a fost ocupat.
O altă abordare: (Abordare optimizată pentru spațiu).
În abordarea de mai sus, folosim doar ultimul rând al matricei 2-D, prin urmare putem optimiza spațiul utilizând
o matrice 2-D cu dimensiunea 2*(min(n,m)).
Mai jos este implementarea abordării de mai sus:
C++
#include> #include> using> namespace> std;> // Function to find the length of the longest LCS> int> LCSubStr(string s, string t,>int> n,>int> m)> {> >// Create DP table> >vectorint>> dp(n + 1, vector |
>
>
Java
// Java implementation of the above approach> import> java.io.*;> class> GFG> {> > >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(String s,String t,> >int> n,>int> m)> >{> > >// Create DP table> >int> dp[][]=>new> int>[>2>][m+>1>];> >int> res=>0>;> > >for>(>int> i=>1>;i<=n;i++)> >{> >for>(>int> j=>1>;j<=m;j++)> >{> >if>(s.charAt(i->1>)==t.charAt(j->1>))> >{> >dp[i%>2>][j]=dp[(i->1>)%>2>][j->1>]+>1>;> >if>(dp[i%>2>][j]>res)> >res=dp[i%>2>][j];> >}> >else> dp[i%>2>][j]=>0>;> >}> >}> >return> res;> >}> > >// Driver Code> >public> static> void> main (String[] args)> >{> >String X=>'OldSite:techcodeview.com.org'>;> >String Y=>'NewSite:GeeksQuiz.com'>;> > >int> m=X.length();> >int> n=Y.length();> > >// Function call> >System.out.println(LCSubStr(X,Y,m,n));> > >}> }> |
>
>
Python3
# Python implementation of the above approach> # Function to find the length of the> # longest LCS> def> LCSubStr(s, t, n, m):> > ># Create DP table> >dp>=> [[>0> for> i>in> range>(m>+> 1>)]>for> j>in> range>(>2>)]> >res>=> 0> > >for> i>in> range>(>1>,n>+> 1>):> >for> j>in> range>(>1>,m>+> 1>):> >if>(s[i>-> 1>]>=>=> t[j>-> 1>]):> >dp[i>%> 2>][j]>=> dp[(i>-> 1>)>%> 2>][j>-> 1>]>+> 1> >if>(dp[i>%> 2>][j]>res):> >res>=> dp[i>%> 2>][j]> >else>:> >dp[i>%> 2>][j]>=> 0> >return> res> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> # Function call> print>(LCSubStr(X,Y,m,n))> # This code is contributed by avanitrachhadiya2155> |
>
>
C#
// C# implementation of the above approach> using> System;> public> class> GFG> {> >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(>string> s,>string> t,> >int> n,>int> m)> >{> >// Create DP table> >int>[,] dp =>new> int>[2, m + 1];> >int> res = 0;> >for>(>int> i = 1; i <= n; i++)> >{> >for>(>int> j = 1; j <= m; j++)> >{> >if>(s[i - 1] == t[j - 1])> >{> >dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;> >if>(dp[i % 2, j]>res)> >res = dp[i % 2, j];> >}> >else> dp[i % 2, j] = 0;> >}> >}> >return> res;> >}> >// Driver Code> >static> public> void> Main (){> >string> X =>'OldSite:techcodeview.com.org'>;> >string> Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >// Function call> >Console.WriteLine(LCSubStr(X,Y,m,n));> >}> }> // This code is contributed by rag2127> |
>
>
Javascript
> // JavaScript implementation of the above approach> >// Function to find the length of the> >// longest LCS> >function> LCSubStr(s, t, n, m)> >{> > >// Create DP table> >var> dp = Array(2).fill().map(()=>Matrice(m+ 1).fill(0));> >var> res = 0;> > >for>(>var> i = 1; i <= n; i++)> >{> >for>(>var> j = 1; j <= m; j++)> >{> >if>(s.charAt(i - 1) == t.charAt(j - 1))> >{> >dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;> >if>(dp[i % 2][j]>res)> >res = dp[i % 2][j];> >}> >else> dp[i % 2][j] = 0;> >}> >}> >return> res;> >}> > >// Driver Code> >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> > >var> m = X.length;> >var> n = Y.length;> > >// Function call> >document.write(LCSubStr(X, Y, m, n));> // This code is contributed by shivanisinghss2110> > |
>
>Ieșire
10>
Complexitatea timpului: O(n*m)
Spațiu auxiliar: O(min(m,n))
O altă abordare: (Folosind recursiunea)
Iată soluția recursivă a abordării de mai sus.
C++
// C++ program using to find length of the> // longest common substring recursion> #include> using> namespace> std;> string X, Y;> // Returns length of function f> // or longest common substring> // of X[0..m-1] and Y[0..n-1]> int> lcs(>int> i,>int> j,>int> count)> {> >if> (i == 0 || j == 0)> >return> count;> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = max(count,> >max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> }> // Driver code> int> main()> {> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.size();> >m = Y.size();> >cout << lcs(n, m, 0);> >return> 0;> }> |
>
număr aleator între 1 și 10
>
Java
// Java program using to find length of the> // longest common substring recursion> import> java.io.*;> class> GFG {> >static> String X, Y;> >// Returns length of function> >// for longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i ==>0> || j ==>0>)> >{> >return> count;> >}> >if> (X.charAt(i ->1>)> >== Y.charAt(j ->1>))> >{> >count = lcs(i ->1>, j ->1>, count +>1>);> >}> >count = Math.max(count,> >Math.max(lcs(i, j ->1>,>0>),> >lcs(i ->1>, j,>0>)));> >return> count;> >}> > >// Driver code> >public> static> void> main(String[] args)> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.length();> >m = Y.length();> >System.out.println(lcs(n, m,>0>));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Python3
# Python3 program using to find length of> # the longest common substring recursion> # Returns length of function for longest> # common substring of X[0..m-1] and Y[0..n-1]> def> lcs(i, j, count):> >if> (i>=>=> 0> or> j>=>=> 0>):> >return> count> >if> (X[i>-> 1>]>=>=> Y[j>-> 1>]):> >count>=> lcs(i>-> 1>, j>-> 1>, count>+> 1>)> >count>=> max>(count,>max>(lcs(i, j>-> 1>,>0>),> >lcs(i>-> 1>, j,>0>)))> >return> count> # Driver code> if> __name__>=>=> '__main__'>:> >X>=> 'abcdxyz'> >Y>=> 'xyzabcd'> >n>=> len>(X)> >m>=> len>(Y)> >print>(lcs(n, m,>0>))> # This code is contributed by Ryuga> |
>
>
C#
// C# program using to find length> // of the longest common substring> // recursion> using> System;> class> GFG {> >static> String X, Y;> >// Returns length of function for> >// longest common substring of> >// X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i == 0 || j == 0) {> >return> count;> >}> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> >// Driver code> >public> static> void> Main()> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.Length;> >m = Y.Length;> >Console.Write(lcs(n, m, 0));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Javascript
> >// Javascript program using to find length of the> >// longest common substring recursion> >let X, Y;> > >// Returns length of function f> >// or longest common substring> >// of X[0..m-1] and Y[0..n-1]> >function> lcs(i, j, count)> >{> > >if> (i == 0 || j == 0)> >return> count;> > >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.max(count,> >Math.max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> > >let n, m;> > >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> > >n = X.length;> >m = Y.length;> > >document.write(lcs(n, m, 0));> > >// This code is contributed by divyeshrabadiya07.> > |
>
>
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>>>> |
>4>
Complexitatea timpului : O(2^max(m,n)) deoarece funcția efectuează două apeluri recursive – lcs(i, j-1, 0) și lcs(i-1, j, 0) când caracterele la X[i-1] != Y[j-1]. Deci, va oferi o complexitate de timp în cel mai rău caz ca 2^N, unde N = max(m, n), m și n este lungimea șirului X și Y.
Spațiu auxiliar: O(1): deoarece apelul funcției nu folosește niciun spațiu suplimentar (funcția folosește doar o stivă de apeluri recursive pe care, în general, nu o luăm în considerare în spațiul auxiliar).
