CEA MAI LUNGĂ SUBSECVENȚĂ COMUNĂ (LCS) - TECHCODEVIEW.COM

Având în vedere două șiruri, S1 și S2 , sarcina este de a găsi lungimea celei mai lungi subsecvențe comune, adică cea mai lungă subsecvență prezentă în ambele șiruri.

A cea mai lungă secvență comună (LCS) este definită ca cea mai lungă subsecvență care este comună în toate secvențele de intrare date.

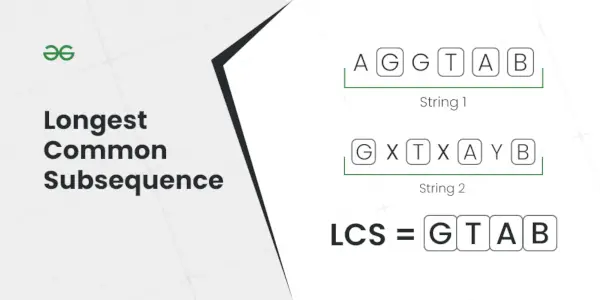
Cea mai lungă subsecvență comună

matrice de structură în limbajul c

Exemple:

Intrare: S1 = ABC, S2 = ACD
Ieșire: 2
Explicaţie: Cea mai lungă subsecvență care este prezentă în ambele șiruri este AC.

Intrare: S1 = AGGTAB, S2 = GXTXAYB
Ieșire: 4
Explicaţie: Cea mai lungă secvență comună este GTAB.

Intrare: S1 = ABC, S2 = CBA
Ieșire: 1
Explicaţie: Există trei subsecvențe comune de lungime 1, A, B și C și nicio subsecvență comună. de lungime mai mare de 1.

Intrare: S1 = XYZW, S2 = XYWZ
Ieșire: 3
Explicaţie: Există două subsecvențe comune de lungime 3 XYZ și XYW și nicio subsecvență comună. cu lungime mai mare de 3.

Practică recomandată Cea mai lungă secvență comună Încercați!

Cea mai lungă subsecvență comună (LCS) folosind recursiunea:

Generați toate subsecvențele posibile și găsiți cea mai lungă dintre ele care este prezentă în ambele șiruri folosind Urmați pașii de mai jos pentru a implementa ideea:

Creați o funcție recursivă [să zicem lcs() ].
Verificați relația dintre primele caractere ale șirurilor care nu au fost încă procesate.
- În funcție de relație, apelați următoarea funcție recursivă așa cum s-a menționat mai sus.
Returnează lungimea LCS primită ca răspuns.

Mai jos este implementarea abordării recursive:

C++

 // A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

 // A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b) ? a:b; } // Cod driver int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0, j = 0;  // Apel de funcție printf('Lungimea LCS este %d', lcs(S1, S2, i, j));  întoarce 0; }>>>Java>>Piton

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b) ? a:b; } // Cod driver public static void Main() { String S1 = 'AGGTAB';  Șirul S2 = 'GXTXAYB';  int m = S1.Lungime;  int n = S2.Lungime;  Console.Write('Lungimea LCS este' + ' ' + lcs(S1, S2, m, n));  } } // Acest cod este Contribuit de Sam007>>>Javascript>>>PHP>>>  
  Ieșire  Length of LCS is 4>
      Complexitatea timpului:    O(2^m+n)  
    Spațiu auxiliar:    O(1)
 Cea mai lungă subsecvență comună (LCS) utilizând  Memorarea : 
 Dacă observăm cu atenție, putem observa că soluția recursivă de mai sus deține următoarele două proprietăți: 
  1. Substructură optimă:
Vezi pentru rezolvarea structurii lui L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) luăm ajutorul substructurilor lui X[0 , 1, …, m-2], Y[0, 1,…, n-2], în funcție de situație (adică folosirea lor optimă) pentru a găsi soluția întregului.
 2. Subprobleme suprapuse:
Dacă folosim abordarea recursivă de mai sus pentru șiruri    BD    și    ABCD    , vom obține un arbore recursiv parțial așa cum se arată mai jos. Aici putem vedea că subproblema L(BD, ABCD) este calculată de mai multe ori. Dacă se ia în considerare arborele total, vor exista mai multe astfel de subprobleme care se suprapun.
  L(AXYT, AYZX)  
/  
L(AXY, AYZX) L(AXYT, AYZ)  
/  /   
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)
 
    Abordare:    Datorită prezenței acestor două proprietăți, putem folosi programarea dinamică sau memorarea pentru a rezolva problema. Mai jos este abordarea soluției folosind recursiunea.
  Creați o funcție recursivă. De asemenea, creați o matrice 2D pentru a stoca rezultatul unei stări unice.
În timpul apelului recursiv, dacă aceeași stare este apelată de mai multe ori, atunci putem returna direct răspunsul stocat pentru acea stare în loc să calculăm din nou.
Mai jos este implementarea abordării de mai sus:
C++ // A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { dacă (m == 0 || n == 0) returnează 0;  dacă (X[m - 1] == Y[n - 1]) returnează dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Cod driver int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  vector> dp(m + 1, vector (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>
 Java /*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>
 Piton # A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>
 C# /* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>b) ? a:b; } public static void Main() { String s1 = 'AGGTAB';  String s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X.Lungime;  int n = Y.Lungime;  int[, ] L = new int[m + 1, n + 1];  pentru (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>
 Javascript /* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>
   
  Ieșire      Complexitatea timpului:    O(m * n) unde m și n sunt lungimile șirurilor.  
    Spațiu auxiliar:    O(m * n) Aici spațiul de stivă recursiv este ignorat.iterator de hartă java
 Cea mai lungă subsecvență comună (LCS) folosind de jos în sus (tabulare):
Putem folosi următorii pași pentru a implementa abordarea de programare dinamică pentru LCS.
 Creați o matrice 2D    dp[][]    cu rânduri și coloane egale cu lungimea fiecărui șir de intrare plus 1 [numărul de rânduri indică indicii de    S1    iar coloanele indică indicii de    S2    ].
Inițializați primul rând și coloană a matricei dp la 0.
Iterați prin rândurile matricei dp, începând de la 1 (să zicem folosind iteratorul    i    ).Pentru fiecare    i    , repetați toate coloanele din    j = 1 la n    :Dacă    S1[i-1]    este egal cu    S2[j-1]    , setați elementul curent al matricei dp la valoarea elementului la (    dp[i-1][j-1] + 1    ).
Altfel, setați elementul curent al matricei dp la valoarea maximă a    dp[i-1][j]    și    dp[i][j-1]    .
După buclele imbricate, ultimul element al matricei dp va conține lungimea LCS.
Consultați ilustrația de mai jos pentru o mai bună înțelegere:
     Ilustrare:    
  Să spunem că șirurile sunt    S1 = AGGTAB    și    S2 = GXTXAYB    .
șir în format java
     Primul pas:    Creați inițial o matrice 2D (să spunem dp[][]) cu dimensiunea 8 x 7 al cărei prim rând și prima coloană sunt umplute cu 0.
  Crearea tabelului dp
    Al doilea pas:    Traverse pentru i = 1. Când j devine 5, S1[0] și S2[4] sunt egale. Deci dp[][] este actualizat. Pentru celelalte elemente ia maximul dp[i-1][j] și dp[i][j-1]. (În acest caz, dacă ambele valori sunt egale, am folosit săgeți la rândurile anterioare).
  Umplerea rândului nr 1
    Al treilea pas:    În timp ce sunt traversate pentru i = 2, S1[1] și S2[0] sunt aceleași (ambele sunt „G”). Deci valoarea dp din acea celulă este actualizată. Restul elementelor sunt actualizate conform condițiilor.
  Umplerea rândului nr. 2
    Al patrulea pas:    Pentru i = 3, S1[2] și S2[0] sunt din nou aceleași. Actualizările sunt după cum urmează.
  Rând de umplere nr. 3
    Al cincilea pas:    Pentru i = 4, putem vedea că S1[3] și S2[2] sunt aceleași. Deci dp[4][3] actualizat ca dp[3][2] + 1 = 2.
  Umplerea rândului 4
    Al șaselea pas:    Aici putem vedea că pentru i = 5 și j = 5 valorile lui S1[4] și S2[4] sunt aceleași (adică, ambele sunt „A”). Deci dp[5][5] este actualizat în consecință și devine 3.
  Umplerea rândului 5
    Ultimul pas:    Pentru i = 6, vezi ultimele caractere ale ambelor șiruri sunt aceleași (sunt „B”). Prin urmare, valoarea lui dp[6][7] devine 4.
  Umplerea ultimului rând
explicați independența datelor
Deci obținem lungimea maximă a subsecvenței comune ca    4    .
 
Mai jos este o implementare tabelată pentru problema LCS.
C++ // Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>
 Java // Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b) ? a:b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Șirul S1 = 'AGGTAB';  Șirul S2 = 'GXTXAYB';  int m = S1.lungime();  int n = S2.lungime();  System.out.println('Lungimea LCS este' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Acest cod este contribuit de Saket Kumar>>>Piton
 C# // Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b) ? a:b; } // Cod driver public static void Main() { String S1 = 'AGGTAB';  Șirul S2 = 'GXTXAYB';  int m = S1.Lungime;  int n = S2.Lungime;  Console.Write('Lungimea LCS este' + ' ' + lcs(S1, S2, m, n));  } } // Acest cod este contribuit de Sam007>>>Javascript
 PHP  // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>>>  
  Ieșire  Length of LCS is 4>
      Complexitatea timpului:    O(m * n) care este mult mai bun decât complexitatea timpului în cel mai rău caz al implementării Naive Recursive.  
    Spațiu auxiliar:    O(m * n) deoarece algoritmul folosește o matrice de dimensiune (m+1)*(n+1) pentru a stoca lungimea subșirurilor comune.
 Cea mai lungă subsecvență comună (LCS) folosind de jos în sus (optimizarea spațiului):
 În abordarea de tabelare de mai sus, folosim L[i-1][j] și L[i][j] etc, aici L[i-1] se va referi la rândul anterior al matricei L și L[i] se referă la rândul curent.
Putem face optimizarea spațiului folosind doi vectori unul este anterior și altul este curent.
Când bucla for internă iese, inițializam anterior egal cu curent.
Mai jos este implementarea:
C++ // Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector prev(m + 1, 0), cur(m + 1, 0);  pentru (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>
 Java // Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>
 Piton def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>
 C# using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>
 Javascript function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>
   
  Ieșire      Complexitatea timpului:    O(m * n), care rămâne același.  
    Spațiu auxiliar:    O(m) deoarece algoritmul folosește două tablouri de dimensiunea m.