Latch este un circuit digital care își convertește instantaneu ieșirea în funcție de intrările sale. Pentru a implementa zăvoare, folosim diferite porți logice. În acest articol, vom vedea definiția zăvoarelor, a tipurilor de zăvor precum SR, gated SR, D, gated D, JK și T cu tabelul de adevăr și diagramele sale, precum și avantajele și dezavantajele zăvorului.
Cuprins
- Ce sunt zăvoarele?
- Tipuri de zăvoare
- SR Latch
- Încuietoare SR cu închidere
- D Latch
- Încuietoare D cu închidere
- JK Latch
- T Latch
- Avantajele zăvoarelor
- Dezavantajele zăvoarelor
Ce sunt zăvoarele?
Latch-urile sunt circuite digitale care stochează un singur bit de informație și își păstrează valoarea până când este actualizat de noi semnale de intrare. Ele sunt utilizate în sistemele digitale ca elemente de stocare temporară pentru stocarea informațiilor binare. Încuietorile pot fi implementate folosind diverse porți logice digitale, cum ar fi ȘI , SAU porțile , NOT, NAND și NOR.
Încuietoarele sunt utilizate pe scară largă în sistemele digitale pentru diverse aplicații, inclusiv stocarea datelor, circuite de control și circuite flip-flop. Ele sunt adesea folosite în combinație cu alte circuite digitale pentru implementare circuite secvențiale , cum ar fi mașinile de stare și elementele de memorie.
Încuietori Definiție
Încuietoarele sunt elemente de stocare de bază care funcționează cu niveluri de semnal (mai degrabă decât tranzițiile semnalului). Încuietorile controlate de o tranziție de ceas sunt papuci flip-flop . Încuietoarele sunt dispozitive sensibile la nivel. Încuietorile sunt utile pentru proiectarea circuit secvenţial asincron . Încuietorile sunt circuite secvenţiale cu două stări stabile. Acestea sunt sensibile la intrare Voltaj aplicat și nu depinde de pulsul ceasului. Flip-flops-urile care nu folosesc impulsul de ceas sunt denumite latch.
Tipuri de încuietori în electronicele digitale
În electronica digitală, diferite tipuri de încuietori sunt:
- Încuietori SR
- Încuietori SR Gated
- D Încuietori
- Încuietori D cu poartă
- Încuietori JK
- T Laches
SR Latch
Încuietori S-R, adică zăvoarele Set-Reset sunt cea mai simplă formă de zăvoare și sunt implementate folosind două intrări: S (Setare) și R (Resetare). Intrarea S setează ieșirea la 1, în timp ce intrarea R resetează ieșirea la 0. Când ambele intrări S și R sunt la 1, se spune că latch-ul este într-o stare nedefinită. Sunt cunoscute și ca stări presetate și clare. Încuietoarea SR formează blocurile de bază ale tuturor celorlalte tipuri de flip-flops.
Tabelul de adevăr al SR Latch
Tabelul de mai jos reprezintă tabelul de adevăr de zăvor SR.
| S | R | Q | Q’ |
|---|---|---|---|
| 0 | 0 | Zăvor | Zăvor |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Diagrama logică a SR Latch
SR Latch este un circuit logic cu:
- 2 porți NOR cuplate în cruce sau 2 porți NAND cuplate încrucișat.
- 2 intrare S pentru SET și R pentru RESET
- 2 ieșire Q, Q’.
Diagrama logică de mai jos reprezintă zăvorul SR folosind Poarta NAND .
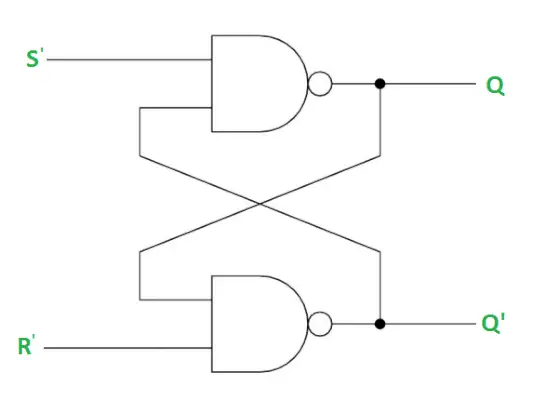
Diagrama logică de mai jos reprezintă utilizarea blocajului SR Poarta NOR .
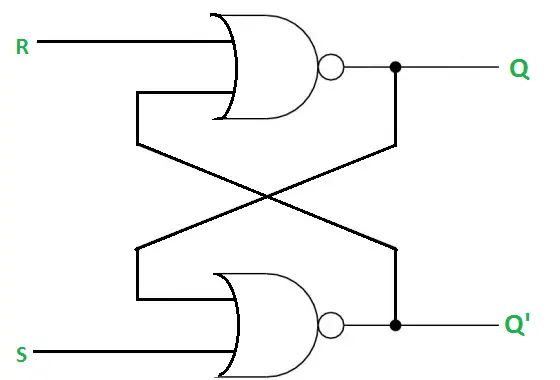
Diferite cazuri de SR Latch
Diferitele cazuri de SR zăvor sunt discutate mai jos.
Cazul 1: S’ = R’ = 1 (S = R = 0)
Dacă Q = 1, intrările Q și R’ pentru a doua poartă NAND sunt ambele 1.
Dacă Q = 0, intrările Q și R’ pentru a doua poartă NAND sunt 0 și, respectiv, 1.

Cazul 2: S’ = 0, R’ = 1 (S = 1, R = 0)
- Ca S’ = 0, ieșirea primei porți NAND, Q = 1 ( stare SET ).
- În a doua poartă NAND, deoarece intrările Q și R’ sunt 1, Q’=0.

Cazul 3: S’ = 1, R’ = 0 (S = 0, R = 1)
- Ca R’=0, ieșirea celei de-a doua porți NAND, Q’ = 1.
- În prima poartă NAND, deoarece intrările Q și S sunt 1, Q = 0 ( starea RESET ).

Cazul 4: S’ = R’ = 0 (S = R = 1)
Când S = R = 1, atât Q, cât și Q’ devin 1, ceea ce nu este permis. Deci, condiția de intrare este interzisă.
Încuietoare SR cu închidere
Un zăvor SR Gated este un zăvor SR cu intrare de activare care funcționează când activarea este 1 și păstrează starea anterioară când activarea este 0.
Tabelul de adevăr al zăvorului SR Gated
Tabelul de mai jos reprezintă tabelul de adevăr al latch-ului Gated SR.
| Permite | S | R git add --all | Qn+1 |
|---|---|---|---|
| 0 | X | X | Qn |
| 1 | 0 | 0 | Qn |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | X |
Diagrama logică a zăvorului SR Gated
Diagrama logică de mai jos reprezintă zăvorul SR cu poartă.

Diagrama logică a zăvorului SR Gated
D Latch
Latch-urile D sunt cunoscute și sub denumirea de latch-uri transparente și sunt implementate folosind două intrări: D (Date) și un semnal de ceas. Ieșirea latch-ului urmează intrarea la terminalul D atâta timp cât semnalul de ceas este ridicat. Când semnalul ceasului scade, ieșirea blocului este stocată și menținută până la următorul front ascendent al ceasului.
Tabelul de adevăr al lui D Latch
Tabelul de mai jos reprezintă tabelul de adevăr al D zăvor.
| ȘI | D | Q | Q’ |
|---|---|---|---|
| 0 | 0 | Zăvor | Zăvor |
| 0 | 1 | Zăvor | Zăvor |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Diagrama logică a D Latch
Diagrama logică de mai jos reprezintă zăvorul D.

Diagrama logică a D Latch
Încuietoare D cu închidere
Încuietoarea D este similară cu zăvorul SR, cu unele modificări făcute. Aici, intrările sunt complementare una pe cealaltă. Latch-ul D reprezintă blocarea datelor, deoarece acest dispozitiv stochează temporar un singur bit.
Tabelul de adevăr al Gated D Latch
Tabelul de mai jos reprezintă tabelul de adevăr al latch-ului Gated D.
| Permite | D | Qn | Qn+1 | STAT |
|---|---|---|---|---|
| 1 | 0 | X | 0 | RESET |
| 1 | 1 | X | 1 | A STABILIT |
| 0 | X | X | Q(n) | Nicio schimbare |
| Ecuația caracteristicilor: Q n+1 = EN.D + EN’.Q n |
Diagrama logică a zăvorului D Gated
Diagrama logică de mai jos reprezintă zăvorul D cu poartă.

JK Latch
Latch-ul JK are două intrări J și K. Ieșirea este comutată când intrările J și K sunt ridicate. JK zăvorul este la fel ca zăvorul SR, dar elimină starea nedefinită a zăvorului SR.
Tabelul de adevăr al lui JK Latch
Tabelul de mai jos reprezintă tabelul de adevăr al JK latch.
| J | K | Qn+1 | cometariu |
|---|---|---|---|
| 0 | 0 | Q | Nicio schimbare |
| 0 | 1 | 0 | Resetați |
| 1 | 0 | 1 | A stabilit |
| 1 | 1 | Q’ | Comutare |
Diagrama logică a JK Latch
Diagrama logică de mai jos reprezintă zăvorul JK.
Diagrama logică a JK Latch
T Latch
Când intrările JK ale JK latch sunt scurtcircuitate, obținem T zăvor. În T latch ieșirile sunt comutate când intrările sunt ridicate.
Diagrama logică a T Latch
Diagrama logică de mai jos reprezintă zăvorul T.
Diagrama logică a T Latch
Avantajele zăvoarelor
Unele dintre avantajele zăvoarelor sunt enumerate mai jos.
- Ușor de implementat: Încuietoarele sunt circuite digitale simple care pot fi implementate cu ușurință folosind baza logica digitala porti.
- Consum redus de putere: Încuietorile consumă mai puțină energie în comparație cu celelalte secvențiale circuite precum flip-flops.
- De mare viteză: Încuietoarele pot funcționa la viteze mari, ceea ce le face potrivite pentru utilizarea în sisteme digitale de mare viteză.
- Cost scăzut: Încuietorile sunt ieftine de fabricat și pot fi utilizate în sisteme digitale cu costuri reduse.
- Versatilitate: Încuietoarele pot fi utilizate pentru diverse aplicații, cum ar fi stocarea datelor, circuite de control și circuite flip-flop.
Dezavantajele zăvoarelor
Unele dintre dezavantajele zăvoarelor sunt enumerate mai jos.
- Fără ceas: Încuietoarele nu au un semnal de ceas pentru a-și sincroniza operațiunile, ceea ce face ca comportamentul lor să fie imprevizibil.
- Stare instabilă: Încuietoarele pot intra uneori într-o stare instabilă când ambele intrări sunt la 1. Acest lucru poate duce la un comportament neașteptat în sistemul digital.
- Timp complex: Momentul zăvoarelor poate fi complex și dificil de specificat, făcându-le mai puțin potrivite pentru aplicațiile de control în timp real.
Concluzie
Putem concluziona că zăvoarele sunt cele mai utilizate în circuitele digitale în diverse scopuri. Latch-urile își modifică rapid ieșirea în raport cu noua intrare. Diferite tipuri de zăvoare includ zăvorul SR, zăvorul cu poartă, zăvorul D, zăvorul D cu zăvor, zăvorul JK și zăvorul T.
Referinţă
Iată câteva cărți la care puteți consulta pentru mai multe informații despre zăvoare:
- Design digital: principii și practici de John F. Wakerly
- Design de sisteme digitale folosind VHDL de Charles H. Roth și Lizy Kurian John
- Analiza și proiectarea circuitelor digitale de Victor P. Nelson și H. Troy Nagle
- Design digital și arhitectură computer de David Harris și Sarah Harris
- Fundamentele logicii digitale cu Verilog Design de Stephen Brown și Zvonko Vranesic
Aceste cărți oferă o imagine de ansamblu cuprinzătoare a logicii digitale, inclusiv zăvoare și acoperă diverse subiecte, cum ar fi proiectarea și implementarea, simularea și verificarea circuitelor digitale.
ELECTRONICA DIGITALĂ – Atul P. Godse, doamna Deepali A. Godse
Încuietori – Întrebări frecvente
Care sunt tipurile de zăvoare?
Tipurile de încuietori includ SR, gated SR, D, gated D, JK și T.
Unde sunt folosite zăvoarele?
Încuietoarele sunt folosite în ceasuri ca unități de depozitare.
dezarhivarea in linux
Câți biți poate stoca un Latch?
Un zăvor poate stoca date pe un bit.
Are Latch memorie?
Da, latch-ul este un element de memorie cu stocare de 1 bit.
