Este fiecare dreptunghi un romb? Dreptunghiul este o figură geometrică bidimensională reprezentată de patru laturi și patru colțuri. Un dreptunghi conține laturi astfel încât lungimea laturilor opuse este egală și aceste laturi sunt paralele între ele. Laturile care împart un colț de la laturile adiacente cu un unghi de 90° între ele. Prin urmare, există patru unghiuri drepte în dreptunghi.

Cuprins
- Dreptunghi
- Romb
- Este fiecare dreptunghi un romb?
- Exemple de întrebări – Fiecare dreptunghi este un romb
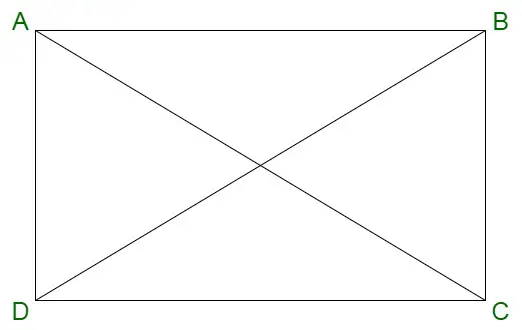
Dreptunghi
Proprietățile unui dreptunghi sunt prezentate mai jos:
- Are patru margini și patru colțuri, cunoscute sub numele de vârfuri.
- Diagonalele unui dreptunghi se bisectează.
- Aria unui dreptunghi este echivalentă cu produsul dintre lungime și lățime.
- Fiecare vârf are un unghi egal cu 90O
- Laturile opuse ale unui dreptunghi sunt egale și paralele între ele.
- Perimetrul este echivalent cu dublul sumei lungimii și lățimii sale.
- Suma tuturor unghiurilor interioare egală cu 360 de grade
Perimetrul unui dreptunghi
Deplasarea totală acoperită prin trecerea prin limita dreptunghiului poate fi numită perimetru. Deoarece atât lungimea, cât și lățimea sunt notate cu unitatea de lungime, perimetrul este, de asemenea, măsurat în unitate de lungime.
Perimetrul poate fi notat cu,
Perimetrul, P = 2 (lungime + lățime)
Zona dreptunghiului
Regiunea acoperită de o figură geometrică bidimensională într-un plan se numește aria unei figuri. Astfel, aria unui dreptunghi este aria inclusă în limitele acestuia. Se măsoară în unități pătrate. Aria este echivalentă cu produsul dintre lungimea și lățimea dreptunghiului.
Aria poate fi notata cu,
Suprafață, A = Lungime × Lățime sq. units
Diagonala unui dreptunghi formulă
Diagonalele oricărei figuri geometrice conectează vârfuri alternative. Lungimea diagonalelor unui dreptunghi poate fi calculată prin următoarea formulă, notată cu d,
d = sqrt{( l^2 + w^2)} Unde,
l = lungimea dreptunghiului
w = lățimea dreptunghiului
Citește în detaliu: Proprietățile dreptunghiului: definiție, formule, exemple
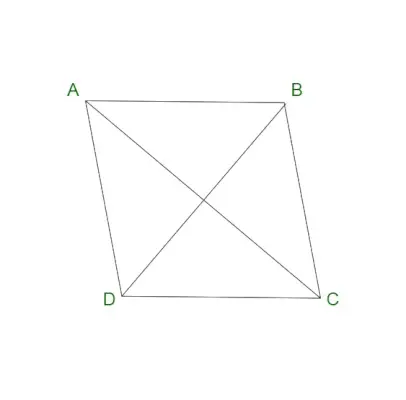
Romb
Un romb este cunoscut și ca patrulater cu patru laturi. Este considerat a fi un caz special de paralelogram. Un romb conține laturi opuse paralele și unghiuri opuse egale. Un romb este cunoscut și sub numele de diamant sau diamant romb. Un romb conține toate laturile unui romb ca lungime egală. De asemenea, diagonalele unui romb se bisectează în unghi drept.
Proprietățile unui romb
Un romb conține următoarele proprietăți:
- Un romb conține toate laturile egale.
- Diagonalele unui romb se bisectează în unghi drept.
- Laturile opuse ale unui romb sunt de natură paralelă.
- Suma a două unghiuri adiacente ale unui romb este egală cu 180O.
- Nu există un cerc de înscriere într-un romb.
- Nu există un cerc circumscris în jurul unui romb.
- Diagonalele unui romb duc la formarea a patru triunghiuri dreptunghiulare.
- Aceste triunghiuri sunt congruente între ele.
- Unghiurile opuse ale unui romb sunt egale.
- Când conectați punctul de mijloc al laturilor unui romb, se formează un dreptunghi.
- Când punctele medii ale jumătății diagonalei sunt conectate, se formează un alt romb.
Perimetrul rombului
Perimetrul unui romb este definit ca lungimea totală a limitelor sale care formează figura. Poate fi, de asemenea, notat ca suma totală a lungimii a patru laturi ale unui romb. Perimetrul unui romb este definit de:
Perimetrul, P = 4a unități
unde diagonalele rombului sunt notate cu d1& d2iar „a” este partea.
Zona rombului
Aria rombului este definită ca regiunea închisă într-un plan bidimensional. Aria unui romb este echivalentă cu produsul dintre diagonalele rombului împărțit la 2. Aria rombului poate fi definită prin următoarea formulă:
Aria, A =
frac{(d_1 imes d_2)}{2} unități mpunde D1și d2sunt diagonalele unui romb.
Putem observa cu ușurință că fiecare romb este un paralelogram, dar inversul nu este adevărat. Un pătrat poate fi considerat un caz special al unui romb, deoarece conține patru laturi de lungime egală. Un pătrat are toate unghiurile drepte. Cu toate acestea, toate unghiurile unui romb nu sunt neapărat unghiuri drepte . În concluzie, un romb care conține unghiuri drepte poate fi considerat un pătrat. Prin urmare, putem spune că,
- Toate romburile sunt paralelograme.
- Toate paralelogramele nu sunt romburi.
- Toate romburi nu sunt pătrate.
- Toate pătratele sunt romburi.
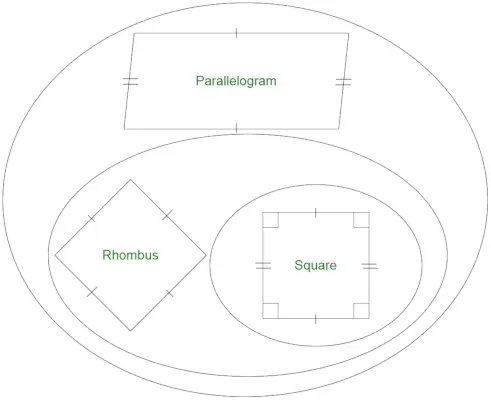
Este fiecare dreptunghi un romb?
Un dreptunghi este o figură geometrică care nu conține toate laturile egale. Un pătrat este un caz special de dreptunghi cu toate laturile egale. Din moment ce, știm, un romb are toate laturile egale. Seturile de dreptunghiuri și romburi se intersectează doar în cazul pătratelor. Prin urmare, dreptunghiul nu este un romb.
șir boolean java

De ce este un romb un dreptunghi?
Un romb este un caz special al unui dreptunghi. Deoarece, știm, că diagonalele unui romb se intersectează la unghiuri egale, în timp ce diagonalele unui dreptunghi sunt egale în lungime. La conectarea punctelor medii ale laturilor unui romb, se formează un dreptunghi.
Citește mai mult: De ce un romb nu este un pătrat?
Exemple de întrebări – Fiecare dreptunghi este un romb
Întrebarea 1. Calculați aria unui cadru dreptunghiular, care are 6 inci lungime și are 3 inci lățime.
Soluţie:
Din moment ce, știm,
Aria unui dreptunghi = (lungime × lățime) unități pătrate.
Înlocuind valorile, obținem,
aria cadrului dreptunghiular = 6 × 3 = 18 inci pătrați
Întrebarea 2. Aflați lungimea diagonalei unui dreptunghi care are lungimea de 12 cm și, respectiv, lățimea de 8 cm.
Soluţie:
Noi stim,
Lungimea diagonală,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Întrebarea 3. Aflați aria unui romb cu cele două lungimi diagonale d 1 și d 2 să fie de 6 cm, respectiv 12 cm.
Soluţie:
Avem,
Diagonala d1= 6 cm
Diagonala d2= 12 cm
Aria rombului este dată de,
A =
frac{(d_1 imes d_2)}{2} unități mpA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Prin urmare, aria rombului = 36 cm2.
Întrebarea 4. Diferența dintre romb și dreptunghi?
Soluţie:
| Proprietate | Romb | Dreptunghi |
| Laturile | Laturi egale. | Laturile opuse sunt egale. |
| Diagonale | Diagonalele se bisectează la 90°. Diagonalele formează unghiuri drepte în centru. | Diagonalele se traversează în unghiuri diferite. Un unghi este un unghi obtuz, iar celălalt este un unghi ascuțit. Diagonalele formează unghiuri diferite în centru – un unghi obtuz și un unghi ascuțit. |
| Unghiuri | Unghiurile opuse sunt egale. Unghiurile adiacente se adaugă până la 180°. | Unghiurile opuse și adiacente sunt egale. Un unghi format de laturile adiacente ale unui dreptunghi este de 90°. |
