Introducere:

O jumătate de sumator este un circuit logic digital care efectuează adăugarea binară a două numere binare pe un singur bit. Are două intrări, A și B și două ieșiri, SUM și CARRY. Ieșirea SUM este bitul cel mai puțin semnificativ (LSB) al rezultatului, în timp ce ieșirea CARRY este bitul cel mai semnificativ (MSB) al rezultatului, indicând dacă a existat un report de la adăugarea celor două intrări. Jumătatea de adunare poate fi implementată folosind porți de bază, cum ar fi porțile XOR și AND.

Sigur, iată o explicație mai aprofundată a circuitului de jumătate de sumator:

Jumătatea de adunare este un element de bază pentru circuite de adunare mai complexe, cum ar fi sumatoarele complete și sumatoarele pe mai mulți biți. Efectuează adăugarea binară a două intrări pe un singur bit, A și B și oferă două ieșiri, SUM și CARRY.

Java regex $

Ieșirea SUM este bitul cel mai puțin semnificativ (LSB) al rezultatului, care este XOR al celor două intrări A și B. Poarta XOR implementează operația de adunare pentru cifre binare, unde un 1 este generat în ieșirea SUM numai atunci când unul dintre intrări este 1.

Ieșirea CARRY este bitul cel mai semnificativ (MSB) al rezultatului, indicând dacă a existat un report de la adăugarea celor două intrări. Ieșirea CARRY este AND-ul celor două intrări A și B. Poarta AND generează un 1 în ieșirea CARRY numai atunci când ambele intrări sunt 1.

Jumătate sumator (HA):

Jumătate de sumator este cel mai simplu dintre toate circuitele de sumator. Jumătate de adunator este un circuit aritmetic combinațional care adună două numere și produce un bit de sumă (s) și un bit de transport (c) ambele ca ieșire. Adăugarea a 2 biți se face utilizând un circuit combinat numit Half Adder. Variabilele de intrare sunt biți augend și addend, iar variabilele de ieșire sunt biți sum & carry. A și B sunt cei doi biți de intrare.

haideți să luăm în considerare doi biți de intrare A și B, apoi suma biților (s) este X-OR al lui A și B. Este evident din funcția de jumătate de sumator că necesită o poartă X-OR și o poartă AND pentru a sa constructie.

Tabelul de adevăr:

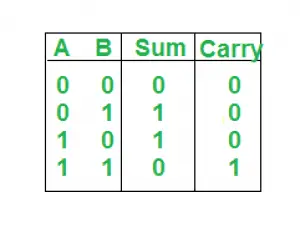
Aici efectuăm două operații Sum și Carry, deci avem nevoie de două K-hărți câte una pentru fiecare pentru a deriva expresia.

Expresie logică:

Pentru suma:

șir împărțit c++

Suma = A XOR B

Pentru transport:

Carry = A ȘI B

Implementare:

Notă: Jumătate de adunare are doar două intrări și nu există nicio prevedere pentru a adăuga o transportare care vine de la biții de ordin inferior atunci când este efectuată adăugarea multiplă.

Avantajele și dezavantajele Half Adder în Digital Logic:

Avantajele Half Adder în logica digitală:

1. Simplitate: O jumătate de viperă este un circuit simplu care necesită câteva părți fundamentale, cum ar fi XOR ȘI intrările. Nu este dificil de realizat și poate fi utilizat în numeroase cadre avansate.

2.Viteza: Jumătate de viperă funcționează extrem de rapid, făcându-l rezonabil pentru utilizare în circuite computerizate rapide.

Dezavantajele Half Adder în logica digitală:

1. Utilitate limitată: Jumătatea viperă poate adăuga două numere dintr-o singură bucată și poate produce un total și un bit de transport. Nu poate efectua extinderea numerelor pe mai mulți biți, ceea ce necesită utilizarea unor circuite complexe suplimentare, cum ar fi sumatoarele complete.

2.Lipsa informațiilor despre transmitere: Jumătate de șarpe nu are o intrare de transmisie, ceea ce îi limitează valoarea în sarcini de expansiune mai uluitoare. O intrare de transmitere este importantă pentru a realiza extinderea numerelor pe mai mulți biți și pentru a înlănțui mai mulți sumatori împreună.

char to string java

3. Amânarea propagării: Circuitul semi-șarpe are o întârziere de proliferare, care este timpul necesar pentru ca rezultatul să se schimbe în lumina unei ajustări a informațiilor. Acest lucru poate cauza probleme de sincronizare în circuitele computerizate, în special în cadrele rapide.

Aplicarea Half Adder în logica digitală:

1.Circuite aritmetice: Jumătățile de adunare sunt utilizate în circuitele de strângere a numărului pentru a adăuga numere duble. În momentul în care diferite jumătăți de adunare sunt asociate într-un lanț, aceștia pot adăuga numere duble pe mai mulți biți.

2. Manipularea datelor: Jumătățile de sumare sunt utilizate în aplicații de manipulare a informațiilor, cum ar fi manipularea computerizată a semnalului, criptarea informațiilor și ajustarea erorilor.

3. Dezlegarea adresei: În cazul memoriei care tinde spre, jumătate de sumatori sunt utilizați în circuitele de descifrare a adreselor pentru a produce locația unei anumite zone de memorie.

4. Circuite de codificator și decodor: Jumătățile de sumare sunt utilizate în circuitele de codificare și decodor pentru cadrele de corespondență computerizate.

5. Multiplexoare și demultiplexoare: Jumătățile de sumare sunt utilizate în multiplexoare și demultiplexoare pentru a alege și informații despre curs.

6.Contoare: Jumătățile de sumatori sunt utilizate în contoare pentru a mări numărul cu unul.