Ce este structura datelor:
O structură de date este o stocare care este utilizată pentru stocarea și organizarea datelor. Este o modalitate de a aranja datele pe un computer astfel încât să poată fi accesate și actualizate eficient.
O structură de date nu este folosită doar pentru organizarea datelor. De asemenea, este folosit pentru procesarea, preluarea și stocarea datelor. În aproape fiecare program sau sistem software care a fost dezvoltat, sunt utilizate diferite tipuri de structuri de date de bază și avansate. Deci trebuie să avem bune cunoștințe ale structurilor de date.
Structuri de date sunt parte integrantă a calculatoarelor utilizate pentru aranjarea datelor în memorie. Ele sunt esențiale și responsabile pentru organizarea, procesarea, accesarea și stocarea eficientă a datelor. Dar asta nu e tot. Diverse tipuri de structuri de date au caracteristicile, caracteristicile, aplicațiile, avantajele și dezavantajele lor. Deci, cum identifici o structură de date care este potrivită pentru o anumită sarcină? Ce se înțelege prin termenul „structură de date”? Câte tipuri de structuri de date există și pentru ce sunt folosite?

Ce este structura datelor: tipuri, clasificări și aplicații
Vă avem acoperit. Am făcut o listă completă cu totul despre ce este structura de date, care sunt tipurile de structuri de date, clasificarea structurilor de date, aplicațiile fiecărei structuri de date și așa mai departe. În acest articol, vom discuta fiecare aspect al fiecărei structuri de date pentru a vă ajuta să alegeți cea mai bună în doar câteva minute.
Cuprins
- Ce este structura datelor?
- Cum diferă structura datelor de tipul de date?
- Clasificarea structurii datelor
- Matrice
- Lista legată
- Grămadă
- Coadă
- Copac
- Grafic
- Concluzie
Cum variază structura datelor de tipul de date:
Am învățat deja despre structura datelor. De multe ori, ceea ce se întâmplă este că oamenii se confundă între tipul de date și structura datelor. Deci, să vedem câteva diferențe între tipul de date și structura datelor pentru a fi clar.
| Tip de date | Structură de date |
|---|---|
| Tipul de date este forma unei variabile căreia i se poate atribui o valoare. Acesta definește că variabila particulară va atribui numai valorile tipului de date dat. | Structura datelor este o colecție de diferite tipuri de date. Toate acele date pot fi reprezentate folosind un obiect și pot fi utilizate în întregul program. |
| Poate deține valoare, dar nu și date. Prin urmare, este fără date. | Poate deține mai multe tipuri de date într-un singur obiect. |
| Implementarea unui tip de date este cunoscută ca implementare abstractă. porniți java | Implementarea structurii de date este cunoscută ca implementare concretă. |
| Nu există complexitate de timp în cazul tipurilor de date. | În obiectele cu structură de date, complexitatea timpului joacă un rol important. |
| În cazul tipurilor de date, valoarea datelor nu este stocată deoarece reprezintă doar tipul de date care pot fi stocate. | În timp ce în cazul structurilor de date, datele și valoarea lor dobândesc spațiul din memoria principală a computerului. De asemenea, o structură de date poate conține diferite tipuri și tipuri de date într-un singur obiect. |
| Exemplele de tipuri de date sunt int, float, double etc. | Exemple de structuri de date sunt stiva, coada, arborele etc. tutoriale java |
Clasificarea structurii datelor:
Structura datelor are multe utilizări diferite în viața noastră de zi cu zi. Există multe structuri de date diferite care sunt utilizate pentru a rezolva diferite probleme matematice și logice. Prin utilizarea structurii de date, se poate organiza și procesa o cantitate foarte mare de date într-o perioadă relativ scurtă. Să ne uităm la diferite structuri de date care sunt utilizate în diferite situații.
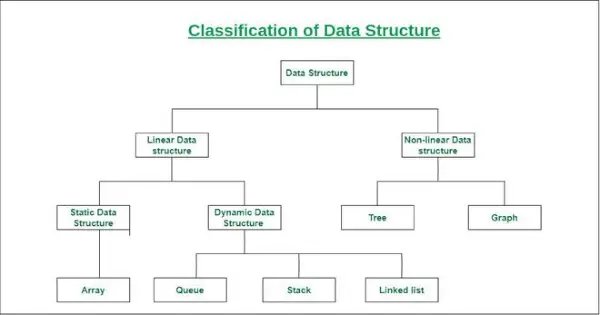
Clasificarea structurii datelor
- Structura liniară a datelor: Structura de date în care elementele de date sunt aranjate secvenţial sau liniar, unde fiecare element este ataşat elementelor sale adiacente anterioare şi următoare, se numeşte structură de date liniară.
Exemple de structuri de date liniare sunt matrice, stivă, coadă, listă legată etc.- Structura statică a datelor: Structura statică de date are o dimensiune de memorie fixă. Este mai ușor să accesați elementele dintr-o structură de date statică.
Un exemplu al acestei structuri de date este o matrice. - Structura dinamică a datelor: În structura dinamică a datelor, dimensiunea nu este fixă. Poate fi actualizat aleatoriu în timpul rulării, ceea ce poate fi considerat eficient în ceea ce privește complexitatea memoriei (spațiului) a codului.
Exemple ale acestei structuri de date sunt coada, stiva etc.
- Structura statică a datelor: Structura statică de date are o dimensiune de memorie fixă. Este mai ușor să accesați elementele dintr-o structură de date statică.
- Structura de date neliniară: Structurile de date în care elementele de date nu sunt plasate secvenţial sau liniar sunt numite structuri de date neliniare. Într-o structură de date neliniară, nu putem traversa toate elementele doar într-o singură rulare.
Exemple de structuri de date neliniare sunt arborii și graficele.
Nevoia de structură a datelor:
Structura datelor și sinteza algoritmului sunt relativ una față de cealaltă. Prezentarea datelor trebuie să fie ușor de înțeles astfel încât dezvoltatorul, precum și utilizatorul, să poată realiza o implementare eficientă a operațiunii.
Structurile de date oferă o modalitate ușoară de organizare, preluare, gestionare și stocare a datelor.
Iată o listă cu nevoile de date.
- Modificarea structurii datelor este ușoară.
- Este nevoie de mai puțin timp.
- Economisiți spațiu de stocare.
- Reprezentarea datelor este ușoară.
- Acces facil la baza de date mare.
Matrice:
O matrice este o structură de date liniară și este o colecție de elemente stocate în locații de memorie adiacente. Ideea este de a stoca mai multe articole de același tip împreună într-un singur loc. Permite procesarea unei cantități mari de date într-o perioadă relativ scurtă. Primul element al matricei este indexat cu un indice de 0. Există diferite operații posibile într-o matrice, cum ar fi Căutarea, Sortarea, Inserarea, Traversarea, Inversarea și Ștergerea.

Matrice
Caracteristicile unui array:
O matrice are diverse caracteristici, care sunt după cum urmează:
- Matricele utilizează o structură de date bazată pe index, care ajută la identificarea cu ușurință a fiecărui element dintr-o matrice folosind indexul.
- Dacă un utilizator dorește să stocheze mai multe valori ale aceluiași tip de date, atunci matricea poate fi utilizată eficient.
- O matrice poate gestiona și structuri complexe de date prin stocarea datelor într-o matrice bidimensională.
- O matrice este, de asemenea, utilizată pentru a implementa alte structuri de date precum stive, cozi, grămezi, tabele Hash etc.
- Procesul de căutare într-o matrice se poate face foarte ușor.
Operații efectuate pe matrice:
- Inițializare : O matrice poate fi inițializată cu valori în momentul declarării sau ulterior folosind o instrucțiune de atribuire.
- Accesarea elementelor: Elementele dintr-o matrice pot fi accesate prin indexul lor, care începe de la 0 și merge până la dimensiunea matricei minus unu.
- Căutarea elementelor : Arrayurile pot fi căutate pentru un anumit element folosind algoritmi de căutare liniară sau binari.
- Sortarea elementelor : Elementele dintr-o matrice pot fi sortate în ordine crescătoare sau descrescătoare folosind algoritmi precum sortarea cu bule, sortarea prin inserție sau sortarea rapidă.
- Inserarea elementelor: Elementele pot fi inserate într-o matrice într-o anumită locație, dar această operație poate consuma mult timp, deoarece necesită mutarea elementelor existente în matrice.
- Ștergerea elementelor: Elementele pot fi șterse dintr-o matrice prin deplasarea elementelor care vin după aceasta pentru a umple golul.
- Elemente de actualizare: Elementele dintr-o matrice pot fi actualizate sau modificate prin atribuirea unei noi valori unui anumit index.
- Elemente de traversare: Elementele dintr-o matrice pot fi parcurse în ordine, vizitând fiecare element o dată.
Acestea sunt unele dintre cele mai frecvente operațiuni efectuate pe matrice. Operațiile și algoritmii specifici utilizați pot varia în funcție de cerințele problemei și de limbajul de programare utilizat.
Aplicații ale matricei:
Diferitele aplicații ale unui tablou sunt următoarele:
- O matrice este utilizată în rezolvarea problemelor matriceale.
- Înregistrările bazelor de date sunt, de asemenea, implementate de o matrice.
- Ajută la implementarea unui algoritm de sortare.
- De asemenea, este folosit pentru a implementa alte structuri de date, cum ar fi stive, cozi, heaps, tabele Hash etc.
- O matrice poate fi utilizată pentru programarea CPU.
- Poate fi aplicat ca tabel de căutare în computere.
- Matricele pot fi utilizate în procesarea vorbirii, unde fiecare semnal de vorbire este o matrice.
- Ecranul computerului este, de asemenea, afișat printr-o matrice. Aici folosim o matrice multidimensională.
- Matricea este utilizată în multe sisteme de management, cum ar fi o bibliotecă, studenți, parlament etc.
- Matricea este utilizată în sistemul online de rezervare a biletelor. Contactele de pe un telefon mobil sunt afișate de această matrice.
- În jocuri precum șahul online, în care jucătorul își poate stoca mișcările trecute, precum și mișcările actuale. Indică un indiciu de poziție.
- Pentru a salva imagini într-o anumită dimensiune în Android, cum ar fi 360*1200
Aplicații reale ale matricei:
- O matrice este folosită frecvent pentru a stoca date pentru calcule matematice.
- Este folosit în procesarea imaginilor.
- Este folosit și în managementul înregistrărilor.
- Paginile de cărți sunt, de asemenea, exemple reale de matrice.
- Se foloseste si la comandarea cutiilor.
Doriți să începeți cu matrice? Puteți încerca articolele și listele noastre organizate pentru cele mai bune practici:
- Introducere în Structura datelor Array
- Top 50 de probleme de codare a matricei pentru interviuri
- Practicați problema Array pe techcodeview.com
Lista legată:
O listă legată este o structură de date liniară în care elementele nu sunt stocate în locații de memorie adiacente. Elementele dintr-o listă legată sunt legate folosind pointeri, așa cum se arată în imaginea de mai jos:
Tipuri de liste legate:
- Listă cu linkuri individuale
- Listă dublu legată
- Listă circulară legată
- Listă dublu circulară legată

Lista legată
Caracteristicile unei liste legate:
O listă legată are diverse caracteristici, care sunt următoarele:
- O listă conectată utilizează memorie suplimentară pentru a stoca link-uri.
- În timpul inițializării listei legate, nu este nevoie să cunoașteți dimensiunea elementelor.
- Listele legate sunt folosite pentru a implementa stive, cozi, grafice etc.
- Primul nod al listei legate se numește Head.
- Următorul indicator al ultimului nod indică întotdeauna spre NULL.
- Într-o listă legată, inserarea și ștergerea sunt posibile cu ușurință.
- Fiecare nod al listei legate constă dintr-un pointer/link care este adresa următorului nod.
- Listele legate se pot micșora sau crește cu ușurință în orice moment.
Operațiuni efectuate pe lista Linked:
O listă legată este o structură de date liniară în care fiecare nod conține o valoare și o referință la următorul nod. Iată câteva operațiuni frecvente efectuate pe listele legate:
- Inițializare: O listă legată poate fi inițializată prin crearea unui nod principal cu o referință la primul nod. Fiecare nod următor conține o valoare și o referință la următorul nod.
- Inserarea elementelor: Elementele pot fi inserate la cap, coadă sau într-o anumită poziție din lista legată.
- Ștergerea elementelor : Elementele pot fi șterse din lista legată prin actualizarea referinței nodului anterior pentru a indica nodul următor, eliminând efectiv nodul curent din listă.
- Căutarea elementelor : Listele legate pot fi căutate pentru un anumit element pornind de la nodul principal și urmând referințele la nodurile următoare până când este găsit elementul dorit.
- Elemente de actualizare : Elementele dintr-o listă legată pot fi actualizate prin modificarea valorii unui anumit nod.
- Elemente de traversare: Elementele dintr-o listă legată pot fi parcurse pornind de la nodul principal și urmând referințele la nodurile următoare până se ajunge la sfârșitul listei.
- Inversarea unei liste conectate : Lista legată poate fi inversată prin actualizarea referințelor fiecărui nod, astfel încât acestea să indice nodul anterior în loc de nodul următor.
Acestea sunt unele dintre cele mai frecvente operațiuni efectuate pe listele legate. Operațiile și algoritmii specifici utilizați pot varia în funcție de cerințele problemei și de limbajul de programare utilizat.
Aplicații ale listei legate:
Diferitele aplicații ale listelor legate sunt următoarele:
- Listele legate sunt folosite pentru a implementa stive, cozi, grafice etc.
- Listele legate sunt folosite pentru a efectua operații aritmetice pe numere întregi lungi.
- Este folosit pentru reprezentarea matricelor rare.
- Este utilizat în alocarea legată de fișiere.
- Ajută la gestionarea memoriei.
- Este folosit în reprezentarea manipulării polinomului în care fiecare termen polinom reprezintă un nod din lista legată.
- Listele legate sunt folosite pentru a afișa containerele de imagini. Utilizatorii pot vizita imaginile trecute, actuale și următoare.
- Sunt folosite pentru a stoca istoricul paginii vizitate.
- Sunt folosite pentru a efectua operațiuni de anulare.
- Linked sunt utilizate în dezvoltarea de software unde indică sintaxa corectă a unei etichete.
- Listele conectate sunt folosite pentru a afișa fluxuri de rețele sociale.
Aplicații reale ale unei liste legate:
- O listă conectată este utilizată în programarea Round-Robin pentru a ține evidența turneului în jocurile multiplayer.
- Este folosit în vizualizatorul de imagini. Imaginile anterioare și următoare sunt legate și, prin urmare, pot fi accesate prin butoanele precedent și următor.
- Într-o listă de redare muzicală, melodiile sunt legate de melodiile anterioare și următoare.
Doriți să începeți cu o listă conectată? Puteți încerca articolele și listele noastre organizate pentru cele mai bune practici:
- Introducere în Structura de date a listelor legate
- Top 20 de întrebări legate de interviu din listă
- Exersați problema Linked List pe techcodeview.com
Grămadă:
Stiva este o structură de date liniară care urmează o anumită ordine în care sunt efectuate operațiunile. Ordinea este LIFO (Ultimul intrat, primul ieşit) . Introducerea și preluarea datelor este posibilă doar de la un capăt. Introducerea și preluarea datelor se mai numește și operație push și pop într-o stivă. Există diferite operații posibile într-o stivă, cum ar fi inversarea unei stive folosind recursiunea, Sortarea, ștergerea elementului din mijloc al unei stive etc.

Grămadă
Caracteristicile unei stive:
Stack are diverse caracteristici diferite, care sunt după cum urmează:
- Stack este folosit în mulți algoritmi diferiți, cum ar fi Turnul din Hanoi, traversarea copacilor, recursiunea etc.
- Stiva este implementată printr-o matrice sau o listă legată.
- Urmează operația Last In First Out, adică un element care este inserat primul va apărea ultimul și invers.
- Inserarea și ștergerea sunt efectuate la un capăt, adică din partea de sus a stivei.
- În stivă, dacă spațiul alocat pentru stivă este plin și totuși cineva încearcă să adauge mai multe elemente, va duce la depășirea stivei.
Aplicații ale stivei:
Diferitele aplicații ale Stivei sunt următoarele:
- Structura de date stiva este utilizată în evaluarea și conversia expresiilor aritmetice.
- Este folosit pentru verificarea parantezelor.
- În timpul inversării unui șir, se folosește și stiva.
- Stiva este folosită în gestionarea memoriei.
- De asemenea, este folosit pentru procesarea apelurilor de funcții.
- Stiva este folosită pentru a converti expresiile din infix în postfix.
- Stiva este folosită pentru a efectua operații de anulare și refacere în procesoarele de text.
- Stiva este utilizată în mașini virtuale precum JVM.
- Stiva este folosită în playerele media. Util pentru a reda melodia următoare și anterioară.
- Stiva este folosită în operațiuni recursive.
Operatie efectuata pe stiva ;
O stivă este o structură de date liniară care implementează principiul Last-In-First-Out (LIFO). Iată câteva operațiuni frecvente efectuate pe stive:
- Apăsaţi : Elementele pot fi împinse în partea de sus a stivei, adăugând un nou element în partea de sus a stivei.
- Pop : Elementul de sus poate fi scos din stivă efectuând o operație pop, eliminând efectiv ultimul element care a fost împins pe stivă.
- Arunca o privire: Elementul superior poate fi inspectat fără a-l scoate din stivă folosind o operație de observare.
- Este gol : Se poate verifica dacă stiva este goală.
- mărimea : Numărul de elemente din stivă poate fi determinat folosind o operație de dimensiune.
Acestea sunt unele dintre cele mai frecvente operațiuni efectuate pe stive. Operațiile și algoritmii specifici utilizați pot varia în funcție de cerințele problemei și de limbajul de programare utilizat. Stivele sunt utilizate în mod obișnuit în aplicații precum evaluarea expresiilor, implementarea stivelor de apeluri de funcție în programe de calculator și multe altele.
Aplicații reale ale stivei:
- Exemplu real de stivă este stratul de farfurii aranjate unul deasupra celuilalt. Când scoateți o farfurie din grămadă, puteți duce farfuria în partea de sus a grămezii. Dar aceasta este exact placa care a fost adăugată cel mai recent la grămadă. Dacă doriți farfuria în partea de jos a grămezii, trebuie să îndepărtați toate plăcile de deasupra pentru a ajunge la ea.
- Browserele folosesc structuri de date stive pentru a ține evidența site-urilor vizitate anterior.
- Jurnalul de apeluri în mobil utilizează, de asemenea, structura de date stiva.
Doriți să începeți cu Stack? Puteți încerca articolele și listele noastre organizate pentru cele mai bune practici:
metoda substring java
- Practicați problema stivei pe techcodeview.com
Coadă:
Coada este o structură de date liniară care urmează o anumită ordine în care sunt efectuate operațiunile. Ordinea este Primul intrat, primul ieşit (FIFO) adică elementul de date stocat primul va fi accesat primul. În aceasta, introducerea și preluarea datelor nu se face doar de la un capăt. Un exemplu de coadă este orice coadă de consumatori pentru o resursă în care consumatorul care a venit primul este servit primul. Pe o coadă sunt efectuate diferite operații, cum ar fi inversarea unei cozi (cu sau fără utilizarea recursiunii), inversarea primelor K elemente ale unei cozi, etc. Câteva operațiuni de bază efectuate în coadă sunt așezare, scoatere la coadă, față, spate etc.
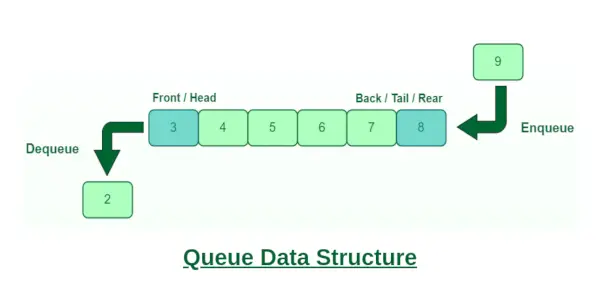
Coadă
Caracteristicile unei cozi:
Coada are diferite caracteristici diferite, care sunt după cum urmează:
- Coada este o structură FIFO (First In First Out).
- Pentru a elimina ultimul element din coadă, toate elementele introduse înaintea noului element din coadă trebuie eliminate.
- O coadă este o listă ordonată de elemente de tipuri de date similare.
Aplicații de coadă:
Diferitele aplicații ale Queue sunt după cum urmează:
- Coada este folosită pentru gestionarea traficului site-ului web.
- Ajută la menținerea listei de redare în playerele media.
- Coada este folosită în sistemele de operare pentru gestionarea întreruperilor.
- Ajută la deservirea cererilor pe o singură resursă partajată, cum ar fi o imprimantă, programarea sarcinilor CPU etc.
- Este utilizat în transferul asincron de date, de ex. țevi, fișiere IO și socluri.
- Cozile sunt folosite pentru programarea lucrărilor în sistemul de operare.
- În rețelele sociale pentru a încărca mai multe fotografii sau videoclipuri este utilizată coada.
- Pentru a trimite o coadă de e-mail este utilizată structura de date.
- Pentru a gestiona traficul pe site-ul web la un moment dat sunt folosite cozi.
- În sistemul de operare Windows, pentru a comuta mai multe aplicații.
Operație efectuată la coadă:
O coadă este o structură de date liniară care implementează principiul First-In-First-Out (FIFO). Iată câteva operațiuni frecvente efectuate pe cozi:
- Pune în coadă : Elementele pot fi adăugate în spatele cozii, adăugând un nou element la sfârșitul cozii.
- În consecinţă : Elementul frontal poate fi eliminat din coadă prin efectuarea unei operații de scoatere din coadă, eliminând efectiv primul element care a fost adăugat în coadă.
- Arunca o privire : Elementul frontal poate fi inspectat fără a-l scoate din coadă folosind o operație de observare.
- Este gol : Se poate verifica dacă coada este goală.
- mărimea : Numărul de elemente din coadă poate fi determinat folosind o operație de dimensiune.
Acestea sunt unele dintre cele mai frecvente operațiuni efectuate pe cozi. Operațiile și algoritmii specifici utilizați pot varia în funcție de cerințele problemei și de limbajul de programare utilizat. Cozile sunt utilizate în mod obișnuit în aplicații precum programarea sarcinilor, gestionarea comunicării între procese și multe altele.
Aplicații reale ale Cozii:
- Un exemplu real de coadă este un drum cu o singură bandă cu sens unic, unde vehiculul care intră primul va ieși primul.
- Un exemplu mai real poate fi văzut în coada de la casele de bilete.
- O linie de casierie într-un magazin este, de asemenea, un exemplu de coadă.
- Oameni pe o scară rulantă
Doriți să începeți cu Queue? Puteți încerca articolele și listele noastre organizate pentru cele mai bune practici:
- Problemă coadă de exersare pe techcodeview.com
Copac:
Un arbore este o structură de date neliniară și ierarhică în care elementele sunt aranjate într-o structură arborescentă. Într-un arbore, nodul cel mai de sus este numit nodul rădăcină. Fiecare nod conține unele date, iar datele pot fi de orice tip. Este format dintr-un nod central, noduri structurale și sub-noduri care sunt conectate prin margini. Structurile de date arborescente diferite permit accesul mai rapid și mai ușor la date, deoarece este o structură de date neliniară. Un arbore are diverse terminologii precum Nod, Rădăcină, Muchie, Înălțimea unui copac, Gradul unui copac etc.
Există diferite tipuri de arbore asemănător
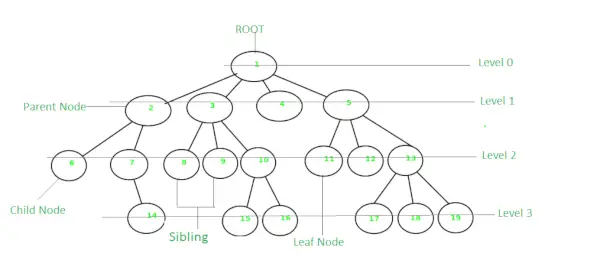
Copac
Caracteristicile unui copac:
Arborele are diferite caracteristici diferite, care sunt după cum urmează:
- Un arbore este cunoscut și ca structură de date recursive.
- Într-un arbore, înălțimea rădăcinii poate fi definită ca cea mai lungă cale de la nodul rădăcină la nodul frunză.
- Într-un copac, se poate calcula și adâncimea de la vârf la orice nod. Nodul rădăcină are o adâncime de 0.
Aplicații ale arborelui:
Diferitele aplicații ale arborelui sunt următoarele:
- Heap este o structură de date arborescentă care este implementată folosind matrice și utilizată pentru a implementa cozile prioritare.
- B-Tree și B+ Tree sunt folosite pentru a implementa indexarea în bazele de date.
- Syntax Tree ajută la scanarea, analizarea, generarea de cod și evaluarea expresiilor aritmetice în proiectarea compilatorului.
- K-D Tree este un arbore de partiție a spațiului folosit pentru a organiza puncte în spațiul K-dimensional.
- Arborele de întindere sunt utilizați în routerele din rețelele de calculatoare.
Operație efectuată pe arbore:
Un arbore este o structură de date neliniară care constă din noduri conectate prin muchii. Iată câteva operațiuni frecvente efectuate pe copaci:
- Inserare : Pot fi adăugate noduri noi la arbore pentru a crea o nouă ramură sau pentru a crește înălțimea arborelui.
- Ștergere : Nodurile pot fi eliminate din arbore prin actualizarea referințelor nodului părinte pentru a elimina referința la nodul curent.
- Căutare : Elementele pot fi căutate într-un arbore pornind de la nodul rădăcină și parcurgând arborele pe baza valorii nodului curent până când este găsit nodul dorit.
- Traversare : Elementele dintr-un arbore pot fi parcurse în mai multe moduri diferite, inclusiv traversarea în ordine, pre-comanda și post-comanda.
- Înălţime : Înălțimea arborelui poate fi determinată prin numărarea numărului de muchii de la nodul rădăcină până la cel mai îndepărtat nod al frunzei.
- Adâncime : Adâncimea unui nod poate fi determinată prin numărarea numărului de muchii de la nodul rădăcină la nodul curent.
- Balansare : Arborele poate fi echilibrat pentru a se asigura că înălțimea arborelui este redusă la minimum și distribuția nodurilor este cât mai uniformă posibil.
Acestea sunt unele dintre cele mai frecvente operațiuni efectuate pe copaci. Operațiile și algoritmii specifici utilizați pot varia în funcție de cerințele problemei și de limbajul de programare utilizat. Arborii sunt utilizați în mod obișnuit în aplicații precum căutarea, sortarea și stocarea datelor ierarhice.
Aplicații reale ale arborelui:
- În viața reală, structura de date arborescentă ajută la dezvoltarea jocului.
- De asemenea, ajută la indexarea în baze de date.
- Un arbore de decizie este un instrument eficient de învățare automată, utilizat în mod obișnuit în analiza deciziilor. Are o structură asemănătoare unei diagrame de flux care ajută la înțelegerea datelor.
- Domain Name Server folosește, de asemenea, o structură de date arborescentă.
- Cel mai frecvent caz de utilizare al unui arbore este orice site de rețea socială.
Vrei să începi cu Tree? Puteți încerca articolele și listele noastre organizate pentru cele mai bune practici:
- Top 50 de întrebări pentru interviul arborelui
- Practicați problema arborelui pe techcodeview.com
Grafic:
Un graf este o structură de date neliniară care constă din vârfuri (sau noduri) și muchii. Este format dintr-un set finit de vârfuri și un set de muchii care conectează o pereche de noduri. Graficul este folosit pentru a rezolva cele mai dificile și complexe probleme de programare. Are terminologii diferite care sunt Calea, Gradul, Nodurile adiacente, Componentele conectate etc.
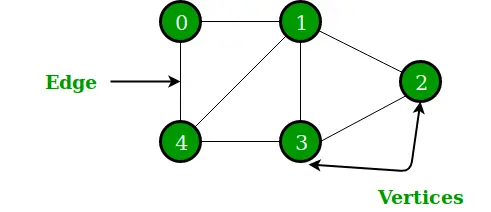
Grafic
Caracteristicile graficului:
Graficul are diferite caracteristici diferite, care sunt după cum urmează:
- Distanța maximă de la un vârf la toate celelalte vârfuri este considerată excentricitatea acelui vârf.
- Vârful cu excentricitate minimă este considerat punctul central al graficului.
- Valoarea minimă a Excentricității din toate vârfurile este considerată raza unui graf conex.
Aplicații ale graficului:
Diferitele aplicații ale graficelor sunt următoarele:
- Graficul este folosit pentru a reprezenta fluxul de calcul.
- Este folosit în modelarea graficelor.
- Sistemul de operare folosește graficul de alocare a resurselor.
- Folosit și în World Wide Web unde paginile web reprezintă nodurile.
Operație efectuată pe Graph:
Un grafic este o structură de date neliniară constând din noduri și muchii. Iată câteva operații frecvente efectuate pe grafice:
- Adăugați un vârf: Pot fi adăugate noi vârfuri la grafic pentru a reprezenta un nou nod.
- Adăugați Edge: Muchiile pot fi adăugate între vârfuri pentru a reprezenta o relație între noduri.
- Eliminați Vertex : Nodurile pot fi eliminate din grafic prin actualizarea referințelor vârfurilor adiacente pentru a elimina referința la vârful curent.
- Eliminați Edge : Muchiile pot fi eliminate prin actualizarea referințelor vârfurilor adiacente pentru a elimina referința la muchia curentă.
- Căutare în profunzime (DFS) : Un grafic poate fi parcurs folosind o căutare depth-first vizitând vârfurile într-o manieră depth-first.
- B readth-Prima căutare (BFS): Un grafic poate fi parcurs folosind o căutare pe lățime, vizitând vârfurile într-o manieră pe lățime.
- Cea mai scurtă cale: Cea mai scurtă cale între două vârfuri poate fi determinată folosind algoritmi precum algoritmul lui Dijkstra sau algoritmul A*.
- Componente conectate : Componentele conectate ale unui graf pot fi determinate prin găsirea de seturi de vârfuri care sunt conectate între ele, dar nu la niciun alt vârf din graf.
- Detectarea ciclului : Ciclurile dintr-un grafic pot fi detectate prin verificarea marginilor din spate în timpul unei căutări în profunzime.
Acestea sunt unele dintre cele mai frecvente operații efectuate pe grafice. Operațiile și algoritmii specifici utilizați pot varia în funcție de cerințele problemei și de limbajul de programare utilizat. Graficele sunt utilizate în mod obișnuit în aplicații precum rețelele de computere, rețelele sociale și problemele de rutare.
Aplicații în viața reală a graficului:
- Unul dintre cele mai comune exemple din lumea reală de grafic este Google Maps, unde orașele sunt situate ca vârfuri și căile care leagă aceste vârfuri sunt situate ca margini ale graficului.
- O rețea socială este, de asemenea, un exemplu real de grafic în care fiecare persoană din rețea este un nod, iar toate prieteniile lor din rețea sunt marginile graficului.
- Un grafic este, de asemenea, folosit pentru a studia moleculele din fizică și chimie.
Doriți să începeți cu Graph? Puteți încerca articolele și listele noastre organizate pentru cele mai bune practici:
multiplexor doi la unul
- Introducere în Structura datelor grafice
- Top 50 de întrebări pentru interviul grafic
- Practicați problema graficului pe techcodeview.com
Avantajele structurii datelor:
- Îmbunătățirea organizării datelor și a eficienței stocării.
- Preluare și manipulare mai rapidă a datelor.
- Facilitează proiectarea algoritmilor pentru rezolvarea problemelor complexe.
- Ușurează sarcina de actualizare și întreținere a datelor.
- Oferă o mai bună înțelegere a relațiilor dintre elementele de date.
Dezavantajul structurii datelor:
- Creșterea supraîncărcării de calcul și de memorie.
- Dificultate în proiectarea și implementarea structurilor complexe de date.
- Scalabilitate și flexibilitate limitate.
- Complexitate în depanare și testare.
- Dificultate în modificarea structurilor de date existente.
Referinţă:
Structurile de date pot fi găsite în diverse manuale de informatică și resurse online. Unele texte populare includ:
- Introducere în algoritmi de Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest și Clifford Stein.
- Structuri de date și analiza algoritmilor în Java de Mark Allen Weiss.
- Manualul de proiectare a algoritmului de Steven S. Skiena.
- Resursele online precum Coursera, Udemy și Khan Academy oferă, de asemenea, cursuri despre structurile de date și algoritmi.
Concluzie
Deși acestea sunt cele mai cunoscute și utilizate structuri de date, există și alte forme de structuri de date care sunt utilizate în informatică, cum ar fi structuri de date bazate pe politici , etc. Dar indiferent de structura de date pe care o alegeți, fiecare are avantajele și dezavantajele sale, fără a ști care, poate fi foarte costisitor să alegeți tipul greșit de structură de date. Prin urmare, este foarte important să înțelegeți nevoia situației și apoi să decideți ce tip de structură de date se potrivește cel mai bine pentru job.
