În primul rând, vom înțelege arbore binar și arbore binar de căutare separat, iar apoi ne vom uita la diferențele dintre un arbore binar și un arbore de căutare binar.
Ce este un arbore binar?
A Arbore binar este o
Arborele binar poate fi reprezentat astfel:
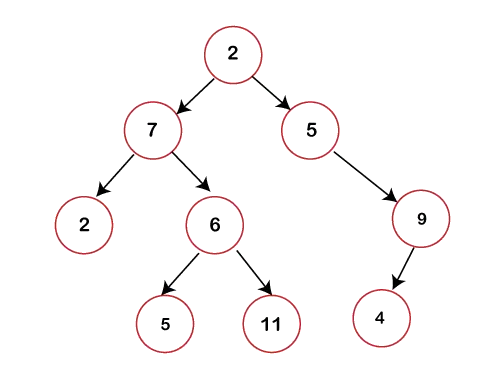
În figura de mai sus, putem observa că fiecare nod conține cel mult 2 copii. Dacă niciun nod nu conține un copil stâng sau drept, atunci valoarea indicatorului în raport cu acel copil ar fi NULL.
Terminologia de bază folosită într-un arbore binar sunt:
Într-un arbore binar, există un arbore cunoscut sub numele de a arbore binar perfect . Este un arbore în care toate nodurile interne trebuie să conțină două noduri, iar toate nodurile frunze trebuie să fie la aceeași adâncime. În cazul unui arbore binar perfect, numărul total de noduri existente într-un arbore binar poate fi calculat utilizând următoarea ecuație:
n = 2m+1-1
unde n este numărul de noduri, m este adâncimea unui nod.
Ce este un arbore de căutare binar?
A Arborele de căutare binar este un arbore care urmează o anumită ordine pentru aranjarea elementelor, în timp ce arborele binar nu urmează nicio ordine. Într-un arbore de căutare binar, valoarea nodului din stânga trebuie să fie mai mică decât nodul părinte, iar valoarea nodului din dreapta trebuie să fie mai mare decât nodul părinte.
Să înțelegem conceptul de arbore binar de căutare prin exemple.

În figura de mai sus, putem observa că valoarea nodului rădăcină este 15, care este mai mare decât valoarea tuturor nodurilor din subarborele din stânga. Valoarea nodului rădăcină este mai mică decât valorile tuturor nodurilor dintr-un subarboresc din dreapta. Acum, trecem la copilul din stânga al nodului rădăcină. 10 este mai mare decât 8 și mai mic decât 12; de asemenea, satisface proprietatea arborelui de căutare binar. Acum, trecem la copilul-dreapta al nodului rădăcină; valoarea 20 este mai mare decât 17 și mai mică decât 25; de asemenea, satisface proprietatea arborelui de căutare binar. Prin urmare, putem spune că arborele prezentat mai sus este arborele binar de căutare.
Acum, dacă schimbăm valoarea de la 12 la 16 în arborele binar de mai sus, trebuie să aflăm dacă este încă un arbore de căutare binar sau nu.

Valoarea nodului rădăcină este 15, care este mai mare decât 10, dar mai mică decât 16, deci nu satisface proprietatea arborelui de căutare binar. Prin urmare, nu este un arbore de căutare binar.
Operații pe arborele de căutare binar
Putem efectua operații de inserare, ștergere și căutare în arborele binar de căutare. Să înțelegem cum se efectuează o căutare pe o căutare binară. Arborele binar este prezentat mai jos pe care trebuie să efectuăm operația de căutare:

Să presupunem că trebuie să căutăm 10 în arborele binar de mai sus. Pentru a efectua căutarea binară, vom lua în considerare toate numerele întregi dintr-o matrice sortată. Mai întâi, creăm o listă completă într-un spațiu de căutare și toate numerele vor exista în spațiul de căutare. Spațiul de căutare este marcat de două indicatori, adică început și sfârșit. Matricea arborelui binar de mai sus poate fi reprezentată ca

Mai întâi, vom calcula elementul din mijloc și vom compara elementul din mijloc cu elementul care urmează să fie căutat. Elementul din mijloc este calculat folosind n/2. Valoarea lui n este 7; prin urmare, elementul din mijloc este 15. Elementul din mijloc nu este egal cu elementul căutat, adică 10.
Notă: Dacă elementul căutat este mai mic decât elementul din mijloc, atunci căutarea va fi efectuată în jumătatea stângă; în rest, căutarea se va face în jumătatea dreaptă. În cazul egalității, elementul este găsit.
Deoarece elementul care trebuie căutat este mai mic decât elementul din mijloc, căutarea va fi efectuată în matricea din stânga. Acum căutarea este redusă la jumătate, după cum se arată mai jos:

Elementul mijlociu din matricea din stânga este 10, care este egal cu elementul căutat.
Complexitatea timpului
Într-o căutare binară, există n elemente. Dacă elementul din mijloc nu este egal cu elementul căutat, atunci spațiul de căutare se reduce la n/2 și vom continua să reducem spațiul de căutare cu n/2 până când găsim elementul. În întreaga reducere, dacă trecem de la n la n/2 la n/4 și așa mai departe, atunci va fi nevoie de log2n trepte.
Diferențele dintre arborele binar și arborele de căutare binar

| Baza pentru comparație | Arbore binar | Arborele de căutare binar |
|---|---|---|
| Definiție | Un arbore binar este o structură de date neliniară în care un nod poate avea cel mult doi copii, adică un nod poate avea 0, 1 sau maximum doi copii. Un arbore binar de căutare este un arbore binar ordonat în care este urmată o anumită ordine pentru a organiza nodurile într-un arbore. | |
| Structura | Structura arborelui binar este că primul nod sau cel mai de sus este cunoscut ca nodul rădăcină. Fiecare nod dintr-un arbore binar conține indicatorul din stânga și indicatorul din dreapta. Indicatorul din stânga conține adresa subarborelui din stânga, în timp ce indicatorul din dreapta conține adresa subarborelui din dreapta. | Arborele de căutare binar este unul dintre tipurile de arbore binar care are valoarea tuturor nodurilor din subarborele din stânga mai mică sau egală cu nodul rădăcină, iar valoarea tuturor nodurilor dintr-un subarboresc din dreapta este mai mare sau egală cu valoarea nodului rădăcină. |
| Operațiuni | Operațiile care pot fi implementate pe un arbore binar sunt inserarea, ștergerea și traversarea. | Arborii binari de căutare sunt arbori binari sortați care asigură inserarea, ștergerea și căutarea rapidă. Căutările implementează în principal căutarea binară, deoarece toate cheile sunt aranjate în ordine sortată. |
| tipuri | Patru tipuri de arbori binari sunt arbore binar complet, arbore binar complet, arbore binar perfect și arbore binar extins. | Există diferite tipuri de arbori binari de căutare, cum ar fi arbori AVL, arbori Splay, arbori Tango etc. |
