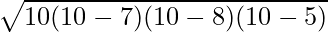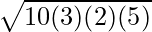Triunghiul unghiular acut este un triunghi în care toate unghiurile triunghiurilor sunt unghiuri ascuțite. Un triunghi poate avea un singur unghi fie ca unghi drept, fie ca unghi obtuz, din cauza proprietății sumei unghiurilor a triunghiului. Și, prin urmare, triunghiul care are toate cele trei unghiuri ca unghiuri ascuțite, adică unghiuri cu o valoare mai mică de 90 de grade, se numește triunghi cu unghi ascuțit.
Pe baza tipurilor de unghiuri interioare ale triunghiului, un triunghi poate fi clasificat în trei categorii, Triunghiuri cu unghi ascuțit, Triunghiuri cu unghi obtuz și Triunghiuri dreptunghiulare. Acum, să aflăm mai multe despre triunghiuri cu unghi ascuți, tipurile, proprietățile și altele în detaliu în acest articol.
Ce este un triunghi cu unghi acut?
Un triunghi unghiular ascutit este definit ca un triunghi ale cărui toate cele trei unghiuri interioare sunt acute, adică valoarea lor este între 0° și 90°. Pe baza tipului de triunghi, lungimile laturilor unui triunghi cu unghi ascuțit pot fi egale sau inegale. Un triunghi unghiular ascuțit urmează, de asemenea, proprietatea sumei unghiurilor a triunghiului.
Figura de mai jos este un triunghi cu unghi ascuțit ale cărui unghiuri interioare sunt 45°, 35° și 80°. Deoarece cele trei unghiuri interioare sunt mai mici de 90°, triunghiul dat este un triunghi cu unghi ascuțit.
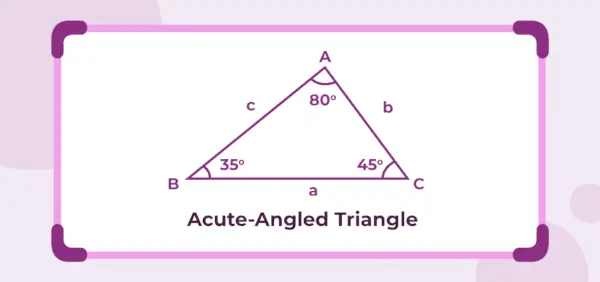
Definiția triunghiului cu unghi acut
Triunghiurile unghiulare ascuțite sunt definite, așa cum sugerează și numele, ca triunghiuri în care toate cele trei unghiuri ale triunghiului sunt unghiuri ascuțite. Latura din triunghiuri cu unghi ascuțit poate fi egală sau inegală și, pe baza acesteia, sunt împărțite în trei părți care sunt discutate în articolul de mai jos,
Tipuri de triunghiuri cu unghi acut
Triunghiurile unghiulare ascuțite sunt clasificate în trei tipuri, în funcție de lungimile laturilor triunghiurilor,
- Triunghi acut echilateral
- Triunghi acut isoscel
- Triunghiul Acut Scalen
Acum să aflăm mai multe despre ele în detaliu.
Triunghi acut echilateral
Un triunghi acut echilateral numit și triunghi echilateral este un triunghi în care toate unghiurile sunt unghiuri ascuțite și toate unghiurile sunt egale, de asemenea, latura triunghiurilor acute echilaterale sunt egale. Fiecare unghi al unui triunghi acut echilateral măsoară întotdeauna 60°.
Triunghi acut isoscel
Un triunghi acut isoscel este un triunghi în care toate unghiurile sunt unghiuri ascuțite și oricare două unghiuri ale triunghiului și latura corespunzătoare acestor unghiuri sunt egale. Adică, în triunghiul acut isoscel avem două laturi și unghiurile corespunzătoare sunt egale.
Triunghiul Acut Scalen
Un triunghi acut scalen este un triunghi în care toate unghiurile sunt unghiuri ascuțite și nu există două unghiuri și nici două laturi egale. Adică, în triunghiul acut scalen nu avem laturi și unghiuri egale.
Proprietățile triunghiului cu unghi acut
Următoarele sunt câteva proprietăți importante ale unui triunghi cu unghi ascuțit,
- Unghiurile interioare ale triunghiului unghiular ascuțit sunt unghiuri ascuțite, adică unghiurile sunt mai mari de 0° dar mai mici de 90°.
- Unghiurile interioare ale triunghiurilor cu unghi ascuți urmează proprietatea sumei unghiurilor, adică suma unghiurilor triunghiului cu unghi ascuți este de 180°.
- Un triunghi echilateral este întotdeauna un triunghi ascuțit, deoarece fiecare unghi interior al unui triunghi echilateral măsoară 60°.
- Un triunghi nu poate fi simultan un triunghi dreptunghic și un triunghi ascuțit.
- Un triunghi nu poate fi simultan un triunghi cu unghi ascuțit și un triunghi cu un unghi obtuz.
- În triunghiul cu unghi ascuțit, latura opusă unghiului cel mai mic este cea mai mică și inversul său este, de asemenea, adevărat.
- În mod similar, latura opusă celui mai mare unghi este cea mai mare și inversul său este, de asemenea, adevărat.
Formule de triunghi cu unghi acut
Aria și perimetrul sunt cele două formule de bază ale unui triunghi unghiular ascuțit care sunt discutate mai jos.
Perimetrul triunghiului cu unghi acut
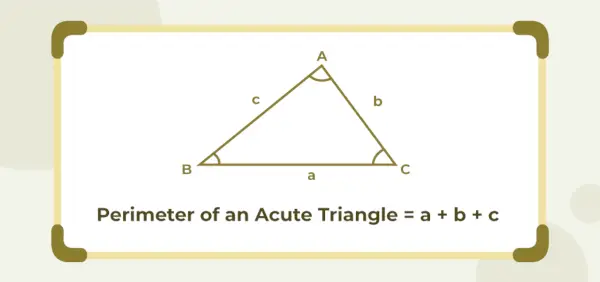
Perimetrul unui triunghi unghiular ascuțit este egal cu suma celor trei lungimi laturi ale sale. Dacă a, b și c sunt lungimile laturilor unui triunghi cu unghi ascuțit, atunci perimetrul acestuia este dat ca unități (a + b + c).
Perimetrul triunghiului acut-unghi = (a + b + c) unități
Unde A , b , și c sunt lungimile laturilor triunghiului.
Citeşte mai mult, Perimetrul unui triunghi
Aria triunghiului cu unghi acut
Aria unui triunghi este definită ca spațiul total cuprins de cele trei laturi ale oricărui triunghi într-un plan bidimensional.
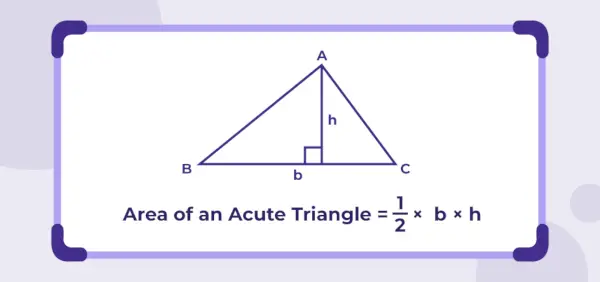
Aria triunghiului cu unghi acut = ½ × b × h
Unde,
b este lungimea bazei șih este înălțimea triunghiului.
Citeşte mai mult, Aria unui triunghi
Zona triunghiului acut după formula lui Heron
Dacă sunt date cele trei lungimi ale laturilor unui triunghi cu unghi ascuțit, atunci aria acestuia poate fi calculată folosind formula lui Heron.
Aria triunghiului acut-unghi =
Unde,
s este semiperimetrul și s = (a + b + c)/2 , tu , b , și c sunt lungimile laturilor triunghiului.
Citeşte mai mult, Formula lui Heron
Terminologii importante ale triunghiului
Diferitele terminologii legate de triunghiul unghiular ascuțit sunt:
În jurul centrului
Centrul cercului care trece de cele trei vârfuri ale triunghiului se numește circumcentrul triunghiului. Se calculează luând punctul de intersecție al bisectoarei perpendiculare. Pentru un triunghi cu unghi ascuțit, circumcentrul se află întotdeauna în interiorul triunghiului.
În centru
Centrul cercului care atinge cele trei laturi ale triunghiului se numește incentrul triunghiului. Se calculează luând punctul de intersecție al bisectoarei unghiulare. Pentru un triunghi cu unghi ascuțit, incentrul se află întotdeauna în interiorul triunghiului.
Centroid
Intersecția medianelor unui triunghi se numește centroidul triunghiului. Pentru un triunghi cu unghi ascuțit, centroidul triunghiului se află întotdeauna în interiorul triunghiului.
Ortocentru
Punctul de intersecție al altitudinii triunghiului se numește ortocentrul triunghiului. Pentru un triunghi cu unghi ascuțit, ortocentrul triunghiului se află întotdeauna în interiorul triunghiului.
Exemple rezolvate pe triunghiul unghiular acut
Exemplul 1: Care dintre următoarele unghiuri poate forma un triunghi cu unghi ascuțit?
- a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°
Soluţie:
Știm că toate unghiurile din triunghiul unghiular ascuțit sunt unghiuri ascuțite, care este măsura lor mai mică de 90 de grade.
Ele urmează, de asemenea, proprietatea sumei unghiurilor a unui triunghi, adică toate unghiurile lor se însumează până la 180 de grade.
A) 65°, 75°, 50°
Aici, toate unghiurile sunt unghiuri ascuțite, dar nu urmează proprietatea sumei unghiurilor, prin urmare triunghiul nu este posibil.
65°+ 75°+ 50° = 190° (triunghiul nu este posibil)
b) 95°, 40°, 45°
Aici triunghiul este posibil, deoarece urmează proprietatea sumei unghiurilor a triunghiului, adică
95°+ 40°+ 45° = 180
Dar în timp ce observăm unghiurile triunghiului am găsit un unghi obtuz de 95°. Prin urmare, triunghiul nu este un triunghi cu unghi ascuțit.
c) 70°, 40°, 70°
Aici triunghiul este posibil, deoarece urmează proprietatea sumei unghiurilor a triunghiului, adică
70°+ 40°+ 70° = 180
Și în timp ce observăm unghiurile triunghiului am constatat că toate unghiurile sunt unghiuri ascuțite. Prin urmare, triunghiul este un triunghi cu unghi ascuțit.
d) 90°, 45°, 45°
Aici triunghiul este posibil, deoarece urmează proprietatea sumei unghiurilor a triunghiului, adică
90°+ 45°+ 45° = 180
Dar în timp ce observăm unghiurile triunghiului am găsit un unghi drept de 90°. Prin urmare, triunghiul nu este un triunghi cu unghi ascuțit.
Exemplul 2: Aflați perimetrul unui triunghi ascuțit XYZ ale cărui laturi sunt XY = 8 unități, YZ = 5 unități și XZ = 9 unități.
care este 10 din 60
Soluţie:
Dat,
Laturile triunghiului acut-unghiular,
- XY(x) = 8 unități
- YZ(y) = 5 unități
- XZ(z) = 9 unități
Noi stim aia,
Perimetrul triunghiului în unghi acut (P) = x + y + z
⇒ P = (8 + 5 + 9) unități
⇒ P = 22 de unități
Prin urmare, perimetrul triunghiului cu unghi ascuțit este de 22 de unități.
Exemplul 3: Aflați aria unui triunghi ascuțit a cărui înălțime este de 12 unități și baza este de 15 unități.
Soluţie:
Dat,
- Înălțimea triunghiului (h) = 12 unități
- Lungimea bazei triunghiului (b) = 15 unități
Noi stim aia,
Aria triunghiului (A) = ½ × b × h
⇒ A = ½ × 12 × 15
⇒ A = ½ × 180
⇒ A = 90 de unități pătrate.
Prin urmare, aria triunghiului acut dat este de 90 de unități pătrate.
Exemplul 4: Aflați aria unui triunghi ascuțit ale cărui laturi sunt AB = 5 cm, BC = 7 cm și AC = 8 cm.
Soluţie:
Dat,
Laturile triunghiului acut-unghiular,
- AB = c = 5 unități
- BC = a = 7 unități
- AC = b = 8 unități
Noi stim aia,
Aria triunghiului =
⇒ A =
⇒ A =
⇒ A = √(300) cm²
⇒ A = 10√3 cm²
Prin urmare, aria triunghiului acut dat este de 10√3 cm2.
Întrebări frecvente despre Triunghiul unghiular acut
Î1: Ce sunt unghiurile acute?
Răspuns:
Unghiurile care variază de la 0° la 90° se numesc unghiuri ascuțite. Adică valoarea minimă a unghiului ascuțit este mai mare de 0° și valoarea maximă a unghiului ascuțit este mai mare de 90°.
Î2: Ce este un triunghi cu unghi acut?
Răspuns:
Un triunghi unghiular ascuțit este un triunghi ale cărui toate cele trei unghiuri interioare sunt unghiuri ascuțite, adică valoarea unghiului este cuprinsă între 0° și 90°.
Î3: Un triunghi echilateral este întotdeauna un triunghi cu unghi acut?
Răspuns:
Da, un triunghi echilateral este întotdeauna un triunghi unghiular ascuțit. Un triunghi unghiular ascuțit sunt unghiurile care au toate unghiurile au unghiuri ascuțite, iar în triunghiul euqilateral toate unghiurile sunt de 60°, adică unghiuri ascuțite. Prin urmare, un triunghi echilateral este întotdeauna un triunghi cu unghi ascuțit.
Î4: Care sunt diferitele tipuri de triunghiuri cu unghi ascuțit?
Răspuns:
Triunghiurile cu unghi ascuți sunt clasificate în trei tipuri care sunt:
- Triunghiul Acut Scalen
- Triunghi acut isoscel
- Triunghi acut echilateral
Î5: Cum să știi dacă un triunghi este un triunghi cu unghi ascuțit?
Răspuns:
Un triunghi ale cărui unghiuri interne sunt mai mici de 90°, adică toate unghiurile interioare sunt unghiuri ascuțite, atunci triunghiul se numește triunghi unghiular ascuțit. Putem verifica dacă triunghiul este triunghi unghiular prin simpla observare a unghiurilor triunghiului.