O stivă este o structură de date liniară care urmează LIFO (ultimul intrat, primul ieșit) principiu. Stiva are un capăt, în timp ce coada are două capete ( din față și din spate ). Conține un singur indicator indicatorul de sus arătând către elementul cel mai de sus al stivei. Ori de câte ori un element este adăugat în stivă, acesta este adăugat în partea de sus a stivei, iar elementul poate fi șters numai din stivă. Cu alte cuvinte, a stiva poate fi definită ca un container în care inserarea și ștergerea se pot face de la un capăt cunoscut ca vârful stivei.

Câteva puncte cheie legate de stiva

• Se numește stivă deoarece se comportă ca o stivă din lumea reală, grămezi de cărți etc.
• O stivă este un tip de date abstracte cu o capacitate predefinită, ceea ce înseamnă că poate stoca elemente de dimensiune limitată.
• Este o structură de date care urmează o anumită ordine de inserare și ștergere a elementelor, iar acea ordine poate fi LIFO sau FILO.

Funcționarea Stivei

Stack funcționează pe modelul LIFO. După cum putem observa în figura de mai jos, există cinci blocuri de memorie în stivă; prin urmare, dimensiunea stivei este 5.

state din SUA

Să presupunem că vrem să stocăm elementele într-o stivă și să presupunem că stiva este goală. Am luat teancul de dimensiunea 5 așa cum se arată mai jos, în care împingem elementele unul câte unul până când teancul se umple.

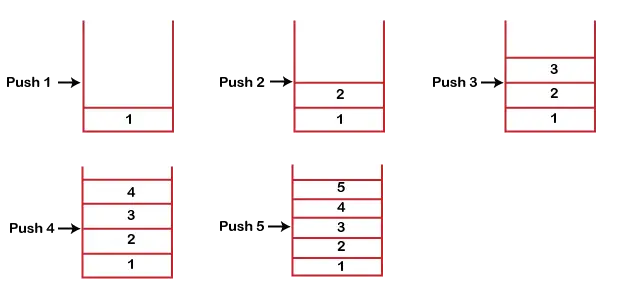
Deoarece stiva noastră este plină, deoarece dimensiunea stivei este de 5. În cazurile de mai sus, putem observa că merge de sus în jos atunci când introducem noul element în stivă. Teancul se umple de jos în sus.

Când efectuăm operația de ștergere pe stivă, există o singură cale de intrare și ieșire, deoarece celălalt capăt este închis. Urmează modelul LIFO, ceea ce înseamnă că valoarea introdusă prima va fi eliminată ultima. În cazul de mai sus, valoarea 5 este introdusă prima, deci va fi eliminată numai după ștergerea tuturor celorlalte elemente.

părtinire și varianță

Operațiuni standard de stivă

Următoarele sunt câteva operațiuni comune implementate pe stivă:

Apăsaţi():Când introducem un element într-o stivă, operația este cunoscută sub numele de împingere. Dacă stiva este plină, atunci apare condiția de depășire.pop():Când ștergem un element din stivă, operația este cunoscută sub numele de pop. Dacă stiva este goală, înseamnă că nu există niciun element în stivă, această stare este cunoscută ca stare de depășire.este gol():Acesta determină dacă stiva este goală sau nu.e plin():Acesta determină dacă stiva este plină sau nu.'arunca o privire():Returnează elementul în poziția dată.numara():Returnează numărul total de elemente disponibile într-o stivă.Schimbare():Schimbă elementul la poziția dată.afişa():Imprimă toate elementele disponibile în stivă.

Operație PUSH

Pașii implicați în operațiunea PUSH sunt prezentați mai jos:

• Înainte de a introduce un element într-o stivă, verificăm dacă stiva este plină.
• Dacă încercăm să introducem elementul într-o stivă, iar stiva este plină, atunci revărsare apare starea.
• Când inițializam o stivă, setăm valoarea top ca -1 pentru a verifica dacă stiva este goală.
• Când noul element este împins într-o stivă, mai întâi, valoarea vârfului este incrementată, adică, sus=sus+1, iar elementul va fi plasat la noua poziţie a top .
• Elementele vor fi introduse până ajungem la max dimensiunea stivei.

Funcționare POP

Pașii implicați în operarea POP sunt prezentați mai jos:

• Înainte de a șterge elementul din stivă, verificăm dacă stiva este goală.
• Dacă încercăm să ștergem elementul din stiva goală, atunci underflow apare starea.
• Dacă stiva nu este goală, accesăm mai întâi elementul care este indicat de top
• Odată ce operația pop este efectuată, partea de sus este decrementată cu 1, adică sus=top-1 .

Aplicații ale Stivei

Următoarele sunt aplicațiile stivei:

Echilibrarea simbolurilor:Stiva este folosită pentru echilibrarea unui simbol. De exemplu, avem următorul program:

 int main() { cout&lt;<'hello'; cout<<'javatpoint'; } < pre> <p>As we know, each program has <em>an opening</em> and <em>closing</em> braces; when the opening braces come, we push the braces in a stack, and when the closing braces appear, we pop the opening braces from the stack. Therefore, the net value comes out to be zero. If any symbol is left in the stack, it means that some syntax occurs in a program.</p> <ul> <tr><td>String reversal:</td> Stack is also used for reversing a string. For example, we want to reverse a &apos; <strong>javaTpoint</strong> &apos; string, so we can achieve this with the help of a stack. <br> First, we push all the characters of the string in a stack until we reach the null character. <br> After pushing all the characters, we start taking out the character one by one until we reach the bottom of the stack. </tr><tr><td>UNDO/REDO:</td> It can also be used for performing UNDO/REDO operations. For example, we have an editor in which we write &apos;a&apos;, then &apos;b&apos;, and then &apos;c&apos;; therefore, the text written in an editor is abc. So, there are three states, a, ab, and abc, which are stored in a stack. There would be two stacks in which one stack shows UNDO state, and the other shows REDO state. <br> If we want to perform UNDO operation, and want to achieve &apos;ab&apos; state, then we implement pop operation. </tr><tr><td>Recursion:</td> The recursion means that the function is calling itself again. To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained. </tr><tr><td>DFS(Depth First Search):</td> This search is implemented on a Graph, and Graph uses the stack data structure. </tr><tr><td>Backtracking:</td> Suppose we have to create a path to solve a maze problem. If we are moving in a particular path, and we realize that we come on the wrong way. In order to come at the beginning of the path to create a new path, we have to use the stack data structure. </tr><tr><td>Expression conversion:</td> Stack can also be used for expression conversion. This is one of the most important applications of stack. The list of the expression conversion is given below: <pre>Infix to prefix Infix to postfix Prefix to infix Prefix to postfix Postfix to infix</pre> </tr><tr><td>Memory management:</td> The stack manages the memory. The memory is assigned in the contiguous memory blocks. The memory is known as stack memory as all the variables are assigned in a function call stack memory. The memory size assigned to the program is known to the compiler. When the function is created, all its variables are assigned in the stack memory. When the function completed its execution, all the variables assigned in the stack are released. </tr></ul> <hr></'hello';>