Premisă - Arborele Fenwick
Știm că pentru a răspunde la întrebările sumelor de gamă de pe un tablou 1-D arbore indexat eficient binar (sau arborele Fenwick) este cea mai bună alegere (chiar mai bună decât arborele segmentului din cauza cerințelor de memorie mai mici și a puțin mai rapid decât arborele segmentului).
Putem răspunde eficient la interogările de sumă sub-matrice folosind arborele indexat binar?
Răspunsul este Da . Acest lucru este posibil folosind un 2d bit Ceea ce nu este altceva decât o serie de bit 1D.
Algoritmul:
Considerăm exemplul de mai jos. Să presupunem că trebuie să găsim suma tuturor numerelor din zona evidențiată:
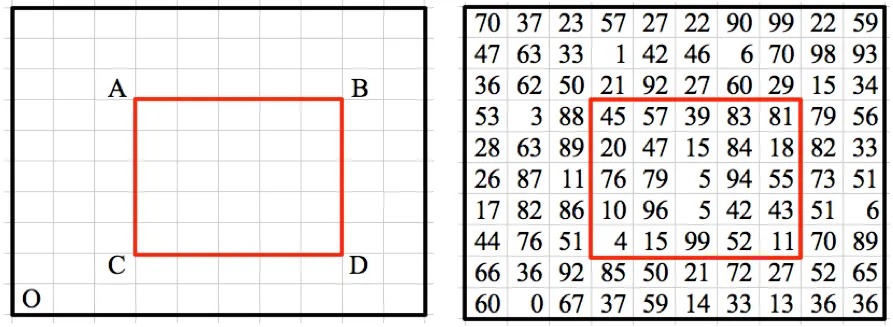
Presupunem originea matricei în partea de jos - o.then un bit 2D exploatează faptul că-
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) 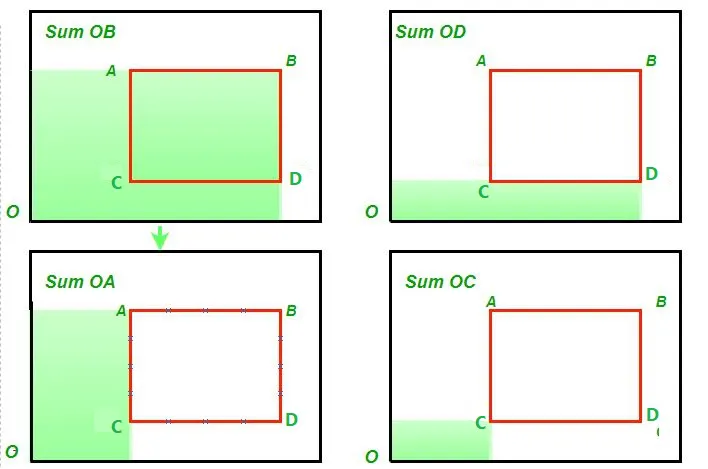
În programul nostru folosim funcția Getsum (x y) care găsește suma matricei de la (0 0) la (x y).
De aici formula de mai jos:
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) The above formula gets reduced to Query(x1y1x2y2) = getSum(x2 y2) - getSum(x2 y1-1) - getSum(x1-1 y2) + getSum(x1-1 y1-1) unde
x1 y1 = x și y coordonate ale lui C
x2 y2 = x și y coordonate ale lui B
Funcția UpdateBit (X Y Val) actualizează toate elementele din regiune - (x y) la (n m) unde
N = maxim x coordonat al întregii matrice.
M = maxim y coordonat al întregii matrice.
Procedura de odihnă este destul de asemănătoare cu cea a 1D Binary Indexed Tree.
Mai jos este implementarea C ++ a arborelui indexat 2D
C++/* C++ program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ #include
/* Java program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ class GFG { static final int N = 4; // N-.max_x and max_y // A structure to hold the queries static class Query { int x1 y1; // x and y co-ordinates of bottom left int x2 y2; // x and y co-ordinates of top right public Query(int x1 int y1 int x2 int y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } }; // A function to update the 2D BIT static void updateBIT(int BIT[][] int x int y int val) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[x][y] += val; } return; } // A function to get sum from (0 0) to (x y) static int getSum(int BIT[][] int x int y) { int sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x][y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux(int mat[][] int aux[][]) { // Initialise Auxiliary array to 0 for (int i = 0; i <= N; i++) for (int j = 0; j <= N; j++) aux[i][j] = 0; // Construct the Auxiliary Matrix for (int j = 1; j <= N; j++) for (int i = 1; i <= N; i++) aux[i][j] = mat[N - j][i - 1]; return; } // A function to construct a 2D BIT static void construct2DBIT(int mat[][] int BIT[][]) { // Create an auxiliary matrix int [][]aux = new int[N + 1][N + 1]; constructAux(mat aux); // Initialise the BIT to 0 for (int i = 1; i <= N; i++) for (int j = 1; j <= N; j++) BIT[i][j] = 0; for (int j = 1; j <= N; j++) { for (int i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum(BIT i j); int v2 = getSum(BIT i j - 1); int v3 = getSum(BIT i - 1 j - 1); int v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries static void answerQueries(Query q[] int m int BIT[][]) { for (int i = 0; i < m; i++) { int x1 = q[i].x1 + 1; int y1 = q[i].y1 + 1; int x2 = q[i].x2 + 1; int y2 = q[i].y2 + 1; int ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); System.out.printf('Query(%d %d %d %d) = %dn' q[i].x1 q[i].y1 q[i].x2 q[i].y2 ans); } return; } // Driver Code public static void main(String[] args) { int mat[][] = { {1 2 3 4} {5 3 8 1} {4 6 7 5} {2 4 8 9} }; // Create a 2D Binary Indexed Tree int [][]BIT = new int[N + 1][N + 1]; construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query q[] = {new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)}; int m = q.length; answerQueries(q m BIT); } } // This code is contributed by 29AjayKumar
'''Python3 program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. ''' N = 4 # N-.max_x and max_y # A structure to hold the queries class Query: def __init__(self x1y1x2y2): self.x1 = x1; self.y1 = y1; self.x2 = x2; self.y2 = y2; # A function to update the 2D BIT def updateBIT(BITxyval): while x <= N: # This loop update all the 1D BIT inside the # array of 1D BIT = BIT[x] while y <= N: BIT[x][y] += val; y += (y & -y) x += (x & -x) return; # A function to get sum from (0 0) to (x y) def getSum(BITxy): sum = 0; while x > 0: # This loop sum through all the 1D BIT # inside the array of 1D BIT = BIT[x] while y > 0: sum += BIT[x][y]; y -= y&-y x -= x&-x return sum; # A function to create an auxiliary matrix # from the given input matrix def constructAux(mataux): # Initialise Auxiliary array to 0 for i in range(N + 1): for j in range(N + 1): aux[i][j] = 0 # Construct the Auxiliary Matrix for j in range(1 N + 1): for i in range(1 N + 1): aux[i][j] = mat[N - j][i - 1]; return # A function to construct a 2D BIT def construct2DBIT(matBIT): # Create an auxiliary matrix aux = [None for i in range(N + 1)] for i in range(N + 1) : aux[i]= [None for i in range(N + 1)] constructAux(mat aux) # Initialise the BIT to 0 for i in range(1 N + 1): for j in range(1 N + 1): BIT[i][j] = 0; for j in range(1 N + 1): for i in range(1 N + 1): # Creating a 2D-BIT using update function # everytime we/ encounter a value in the # input 2D-array v1 = getSum(BIT i j); v2 = getSum(BIT i j - 1); v3 = getSum(BIT i - 1 j - 1); v4 = getSum(BIT i - 1 j); # Assigning a value to a particular element # of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); return; # A function to answer the queries def answerQueries(qmBIT): for i in range(m): x1 = q[i].x1 + 1; y1 = q[i].y1 + 1; x2 = q[i].x2 + 1; y2 = q[i].y2 + 1; ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); print('Query (' q[i].x1 ' ' q[i].y1 ' ' q[i].x2 ' ' q[i].y2 ') = ' ans sep = '') return; # Driver Code mat= [[1 2 3 4] [5 3 8 1] [4 6 7 5] [2 4 8 9]]; # Create a 2D Binary Indexed Tree BIT = [None for i in range(N + 1)] for i in range(N + 1): BIT[i]= [None for i in range(N + 1)] for j in range(N + 1): BIT[i][j]=0 construct2DBIT(mat BIT); ''' Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 ''' q = [Query(1 1 3 2) Query(2 3 3 3) Query(1 1 1 1)]; m = len(q) answerQueries(q m BIT); # This code is contributed by phasing17
/* C# program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by.Adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and.Adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ using System; class GFG { static readonly int N = 4; // N-.max_x and max_y // A structure to hold the queries public class Query { public int x1 y1; // x and y co-ordinates of bottom left public int x2 y2; // x and y co-ordinates of top right public Query(int x1 int y1 int x2 int y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } }; // A function to update the 2D BIT static void updateBIT(int []BIT int x int y int val) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[xy] += val; } return; } // A function to get sum from (0 0) to (x y) static int getSum(int []BIT int x int y) { int sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux(int []mat int []aux) { // Initialise Auxiliary array to 0 for (int i = 0; i <= N; i++) for (int j = 0; j <= N; j++) aux[i j] = 0; // Construct the Auxiliary Matrix for (int j = 1; j <= N; j++) for (int i = 1; i <= N; i++) aux[i j] = mat[N - j i - 1]; return; } // A function to construct a 2D BIT static void construct2DBIT(int []mat int []BIT) { // Create an auxiliary matrix int []aux = new int[N + 1 N + 1]; constructAux(mat aux); // Initialise the BIT to 0 for (int i = 1; i <= N; i++) for (int j = 1; j <= N; j++) BIT[i j] = 0; for (int j = 1; j <= N; j++) { for (int i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum(BIT i j); int v2 = getSum(BIT i j - 1); int v3 = getSum(BIT i - 1 j - 1); int v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[ij] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries static void answerQueries(Query []q int m int []BIT) { for (int i = 0; i < m; i++) { int x1 = q[i].x1 + 1; int y1 = q[i].y1 + 1; int x2 = q[i].x2 + 1; int y2 = q[i].y2 + 1; int ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); Console.Write('Query({0} {1} {2} {3}) = {4}n' q[i].x1 q[i].y1 q[i].x2 q[i].y2 ans); } return; } // Driver Code public static void Main(String[] args) { int []mat = { {1 2 3 4} {5 3 8 1} {4 6 7 5} {2 4 8 9} }; // Create a 2D Binary Indexed Tree int []BIT = new int[N + 1N + 1]; construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query []q = {new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)}; int m = q.Length; answerQueries(q m BIT); } } // This code is contributed by Rajput-Ji
<script> /* Javascript program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ let N = 4; // N-.max_x and max_y // A structure to hold the queries class Query { constructor(x1y1x2y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } } // A function to update the 2D BIT function updateBIT(BITxyval) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[x][y] += val; } return; } // A function to get sum from (0 0) to (x y) function getSum(BITxy) { let sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x][y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix function constructAux(mataux) { // Initialise Auxiliary array to 0 for (let i = 0; i <= N; i++) for (let j = 0; j <= N; j++) aux[i][j] = 0; // Construct the Auxiliary Matrix for (let j = 1; j <= N; j++) for (let i = 1; i <= N; i++) aux[i][j] = mat[N - j][i - 1]; return; } // A function to construct a 2D BIT function construct2DBIT(matBIT) { // Create an auxiliary matrix let aux = new Array(N + 1); for(let i=0;i<(N+1);i++) { aux[i]=new Array(N+1); } constructAux(mat aux); // Initialise the BIT to 0 for (let i = 1; i <= N; i++) for (let j = 1; j <= N; j++) BIT[i][j] = 0; for (let j = 1; j <= N; j++) { for (let i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array let v1 = getSum(BIT i j); let v2 = getSum(BIT i j - 1); let v3 = getSum(BIT i - 1 j - 1); let v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries function answerQueries(qmBIT) { for (let i = 0; i < m; i++) { let x1 = q[i].x1 + 1; let y1 = q[i].y1 + 1; let x2 = q[i].x2 + 1; let y2 = q[i].y2 + 1; let ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); document.write('Query ('+q[i].x1+' ' +q[i].y1+' ' +q[i].x2+' ' +q[i].y2+') = ' +ans+'
'); } return; } // Driver Code let mat= [[1 2 3 4] [5 3 8 1] [4 6 7 5] [2 4 8 9]]; // Create a 2D Binary Indexed Tree let BIT = new Array(N + 1); for(let i=0;i<(N+1);i++) { BIT[i]=new Array(N+1); for(let j=0;j<(N+1);j++) { BIT[i][j]=0; } } construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ let q = [new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)]; let m = q.length; answerQueries(q m BIT); // This code is contributed by rag2127 </script>
Ieșire
Query(1 1 3 2) = 30 Query(2 3 3 3) = 7 Query(1 1 1 1) = 6
Complexitate a timpului:
- Atât funcția UpdateBit (x y val), cât și funcția Getsum (x y) necesită o (log (n)*log (m)) timp.
- Construirea bitului 2D ia o (nm jurnal (n)*log (m)).
- Întrucât în fiecare dintre întrebările apelăm la funcții Getsum (x y), astfel încât să răspundem la toate întrebările Q O (Q*log (n)*log (m)) timp.
- Prin urmare, complexitatea generală a timpului este O ((nm+q)*log (n)*log (m)) unde
N = maxim x coordonat al întregii matrice.
M = maxim y coordonat al întregii matrice.
Q = numărul de întrebări.
Spațiu auxiliar: O (nm) pentru a stoca bitul și tabloul auxiliar
