Frecarea este o forță care rezistă mișcării relative și are loc la interfața dintre corpuri, dar și în interiorul corpurilor, ca în cazul fluidelor. Conceptul de coeficient de frecare a fost formulat pentru prima dată de Leonardo da Vinci. Mărimea coeficientului de frecare este determinată de proprietățile suprafețelor, împrejurimile, caracteristicile suprafeței, prezența lubrifiantului etc.
Legile frecării
Există cinci legi ale frecării și acestea sunt:
• Frecarea obiectului în mișcare este proporțională și perpendiculară pe forța normală.
• Frecarea experimentată de obiect depinde de natura suprafeței cu care este în contact.
• Frecarea este independentă de zona de contact atâta timp cât există o zonă de contact.
• Frecarea cinetică este independentă de viteză.
• Coeficientul de frecare statică este mai mare decât coeficientul de frecare cinetică.
Când vedem orice obiect, putem vedea suprafața netedă, dar când același obiect este privit la microscop, se poate observa că chiar și obiectul care apare neted are margini aspre. Dealurile și șanțurile mici pot fi văzute prin microscop și sunt cunoscute ca neregularități ale suprafeței. Deci, atunci când un obiect este mutat peste celălalt, aceste neregularități de pe suprafață se încurcă, dând naștere la frecare. Mai multă rugozitatea, cu atât mai multe neregulile vor fi și mai mare va fi forța aplicată.
Frecare statică
Există mai multe teorii cu privire la cauzele frecării statice și, la fel ca majoritatea conceptelor legate de frecare, fiecare se dovedește valabilă în anumite condiții, dar eșuează în alte circumstanțe. Pentru aplicații din lumea reală (în special cele legate de mașini industriale și mișcare). Controlul celor două teorii cele mai larg acceptate din spatele frecării statice au de-a face cu rugozitatea microscopică a suprafețelor.
Indiferent de cât de perfect este prelucrată, finisată și curățată o suprafață, aceasta va avea inevitabil asperități – în esență rugozitate, constând din vârfuri și văi, la fel ca un lanț muntos. (Din punct de vedere tehnic, vârfurile sunt asperitățile.) Când două suprafețe sunt în contact, poate părea că au o zonă mare de contact bine definită, dar, în realitate, contactul are loc doar în anumite locuri – adică acolo unde asperitățile ambele suprafete interfereaza.
Suma acestor zone mici de contact dintre asperități este denumită zona de contact reală sau efectivă. Deoarece aceste zone individuale de contact sunt foarte mici, presiunea (presiune = forță ÷ suprafață) dintre suprafețe în aceste puncte este foarte mare. Această presiune extremă permite aderența între suprafețe, printr-un proces cunoscut sub numele de sudare la rece, care are loc la nivel molecular. Înainte ca suprafețele să se poată mișca una față de cealaltă, trebuie rupte legăturile care provoacă această aderență.
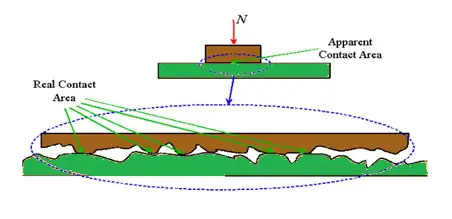
În plus, rugozitatea suprafețelor înseamnă că, în unele locații, asperitățile unei suprafețe se vor așeza în văile celeilalte suprafețe - cu alte cuvinte, suprafețele se vor interconecta.
Aceste zone interblocate trebuie sparte sau deformate plastic înainte ca suprafețele să se poată mișca. Cu alte cuvinte, trebuie să apară abraziunea. Deci, în majoritatea aplicațiilor, frecarea statică este cauzată atât de aderența, cât și de abraziunea suprafețelor de contact.
Legile frecării statice
Există două legi ale frecării statice:
- Prima lege: Forța maximă de frecare statică nu depinde de zona de contact.
- A doua lege: Forța maximă a frecării statice este comparativă cu forța normală, adică dacă forța normală crește, crește și forța externă maximă pe care o poate suporta obiectul fără a se mișca.

Derivarea formulei frecării statice
Să luăm în considerare un bloc de greutate mg situat pe o suprafață orizontală, așa cum se arată în figură. Atunci când un corp apasă pe o suprafață, suprafața se deformează chiar dacă pare a fi rigidă. Suprafața deformată împinge corpul cu o forță normală R care este perpendiculară pe suprafață. Aceasta se numește forță de reacție normală. Echilibrează mg adică
R = mg
Acum să considerăm că pe bloc se aplică o forță P. În mod clar corpul rămâne în repaus, deoarece o altă forță F intră în joc în direcția orizontală și se opune forței aplicate P, rezultând forța netă zero asupra corpului. Această forță F care acționează de-a lungul suprafeței corpului în contact cu suprafața mesei se numește forță de frecare.
Deci, atâta timp cât corpul nu se mișcă F = P. Aceasta înseamnă că dacă creștem P, crește și frecarea F, rămânând întotdeauna egală cu P.
Această forță de frecare care intră în joc până când mișcarea reală începe este cunoscută sub numele de frecare statică.
Coeficientul de frecare statică
Frecarea statică este frecarea care apare atunci când un obiect este plasat pe o suprafață. Și, frecarea cinetică se datorează mișcării unui obiect pe o suprafață. Frecarea este bine caracterizată de coeficientul de frecare și este explicată ca raportul dintre forța de frecare și forța normală. Acest lucru ajută obiectul să se așeze pe o suprafață. Coeficientul de frecare statică este o mărime scalară și notat cu μs.
Formula pentru coeficientul de frecare statică este exprimată ca
mu_{s} = frac{F}{N} Unde
m s = coeficientul de frecare statică
F = forța de frecare statică
N = forta normala

Frecare cinetică
Frecarea cinetică este definită ca o forță care acționează între suprafețele în mișcare. Un corp care se mișcă la suprafață experimentează o forță în direcția opusă mișcării sale. Mărimea forței va depinde de coeficientul de frecare cinetică dintre cele două materiale.
Frecarea este ușor de definită ca forța care reține un obiect care alunecă. Frecarea cinetică face parte din tot și interferează mișcarea a două sau mai multe obiecte. Forța acționează în direcția opusă modului în care un obiect vrea să alunece.
Dacă o mașină trebuie să se oprească, aplicăm frânele și exact acolo intră în joc frecarea. În timpul mersului, când cineva vrea să se oprească brusc, frecarea înseamnă a mulțumi din nou. Dar când trebuie să ne oprim în mijlocul unei bălți, lucrurile devin mai dificile, deoarece frecarea este mai mică și nu poate ajuta atât de mult.

Depășirea frecării statice dintre două suprafețe îndepărtează în esență atât obstacolele moleculare (sudarea la rece între asperități), cât și, într-o oarecare măsură, obstacolele mecanice (Interferența dintre asperitățile și văile suprafețelor) la mișcare. Odată inițiată mișcarea, o oarecare abraziune continuă să apară, dar la un nivel mult mai scăzut decât în timpul frecării statice și viteza relativă dintre suprafețe oferă timp insuficient pentru a avea loc o sudură suplimentară la rece (cu excepția cazului de viteză extrem de scăzută).
Cu cea mai mare parte a aderenței și abraziunii fiind depășite pentru a induce mișcarea, rezistența la mișcare între suprafețe este redusă, iar suprafețele se mișcă acum sub influența frecării cinetice, care este mult mai mică decât frecarea statică.
Legile frecării cinetice
Există patru legi ale frecării cinetice:
- Prima lege: Forța de frecare cinetică (Fk) este direct proporțională cu reacția normală (N) dintre două suprafețe în contact. Unde, m k = constantă numită coeficient de frecare cinetică.
- A doua lege: Forța de frecare cinetică este independentă de forma și suprafața aparentă a suprafețelor în contact.
- A treia lege: Depinde de natura și materialul suprafeței în contact.
- A patra lege: Este independent de viteza obiectului în contact cu condiția ca viteza relativă dintre obiect și suprafață să nu fie prea mare.

Formula de frecare cinetică
Coeficientul de frecare cinetică este notat cu litera greacă mu ( m ), cu un indice k. Forța de frecare cinetică este m k ori mai mare decât forța normală asupra unui corp. Se exprimă în Newton (N).
Ecuația frecării cinetice poate fi scrisă astfel:
Forța de frecare cinetică = (coeficient de frecare cinetică) (forța normală)
F k = m k h
Unde,
F k = forța de frecare cinetică
m k coeficientul de frecare cinetică
h = forță normală (litera greacă eta)

Derivarea formulei frecării cinetice
Să luăm în considerare un bloc de greutate mg culcat pe o suprafață orizontală, așa cum se arată în figură. Când un corp apasă pe o suprafață, suprafața se deformează chiar dacă pare a fi rigidă. Suprafața deformată împinge corpul cu o forță normală R care este perpendicular pe suprafata. Aceasta se numește forță de reacție normală. Echilibrează mg adică R = mg .
testare și tipuri de testare
Acum să considerăm asta o forță P se aplică pe bloc așa cum se arată. În mod clar, corpul rămâne în repaus din cauza unei alte forțe F intră în joc în direcția orizontală și se opune forței aplicate P rezultând forța netă zero asupra corpului. Această forță F care acționează de-a lungul suprafeței corpului în contact cu suprafața mesei se numește forță de frecare .
Deci atâta timp cât corpul nu se mișcă F = P . Aceasta înseamnă că dacă creștem P, crește și frecarea F, rămânând întotdeauna egală cu P.
Pe măsură ce creștem forța aplicată ușor dincolo de limitarea frecării, începe mișcarea reală. Aceasta nu înseamnă că frecarea a dispărut. Înseamnă doar că forța a depășit frecarea limitatoare. Această forță de frecare în această etapă este cunoscută sub denumirea de frecare cinetică sau frecare dinamică.
Frecarea cinetică sau frecarea dinamică este forța opusă care intră în joc atunci când corpul se mișcă de fapt pe suprafața altui corp.
Aplicarea frecării statice și cinetice

Aplicații ale frecării statice
Câteva exemple din viața reală de frecare statică sunt date în punctele de mai jos:
- Hârtii pe o masă
- Un prosop atârnat pe un suport
- Un marcaj într-o carte
- O mașină parcata pe un deal
Aplicații ale frecării cinetice
Câteva exemple din viața reală de frecare cinetică sunt date în punctele de mai jos.
- Frecarea joacă, de asemenea, un rol important în evenimentele de zi cu zi, cum ar fi atunci când are loc frecarea a două obiecte. Mișcarea rezultată se transformă în căldură și, astfel, rezultă în incendiu în unele cazuri.
- De asemenea, este responsabil pentru uzură și de aceea avem nevoie de ulei pentru a lubrifia piesele mașinii, deoarece reduce frecarea.
- Când două obiecte sunt frecate unul de celălalt, forța de frecare este transformată în energie termică, în câteva cazuri dând naștere la foc.
- Frecarea cinetică este responsabilă pentru uzura pieselor mașinii, de aceea este important să lubrifiați piesele mașinii cu ulei.
Diferența dintre frecarea statică și cinetică
| Frecare statică | Frecare cinetică |
| Frecarea statică este frecarea prezentă între două sau mai multe obiecte care nu se mișcă unul față de celălalt | Frecarea cinetică este frecarea prezentă între două sau mai multe obiecte care sunt în mișcare unul față de celălalt. |
| Mărimea frecării statice este mai mare datorită valorii mai mari a coeficientului său. | Mărimea frecării cinetice este comparativ mai mică datorită valorii scăzute a coeficientului său. |
Ecuația care reprezintă frecarea statică este dată de Fs= msh | Ecuația care reprezintă frecarea cinetică este dată de Fk= mkh |
| Valoarea sa poate fi zero. | Valoarea sa nu poate fi niciodată zero. |
| Exemplu - Un creion pe masă. | Exemplu - Mutarea creionului peste o masă. |
Exemple de probleme bazate pe frecare statică și cinetică
Întrebarea 1: Un bărbat împinge pe podea un carton mare de 75,0 kg.
Soluţie:
Coeficientul de frecare cinetică este μk= 0,520
Muncitorul exercită o forță de 400,0 N înainte.
Care este magnitudinea forței de frecare?
Răspuns: Pe o suprafață plană, forța normală a unui obiect poate fi găsită prin formula
h = mg
Prin înlocuirea valorii lui η în ecuația Fk= mkη, obținem
Fk= (0,520) (75,0 kg) (9,80 m/s2) = 382,2N
Întrebarea 2: În întrebarea de mai sus, calculați forța netă care mișcă cutia?
Soluţie:
Forța netă care acționează asupra unui corp este suma tuturor forțelor care acționează asupra corpului.
In acest caz, fortele care actioneaza asupra corpului sunt forta exercitata de om si frecarea cinetica care actioneaza in sens invers.
Dacă mișcarea înainte este considerată pozitivă, atunci forța netă se calculează după cum urmează:
Fnet= Fmuncitor– Fk
Înlocuind valorile din ecuația de mai sus, obținem
Fnet= 400 N – 382,2 N = 17,8 N
Întrebarea 3: De ce mișcarea de rulare experimentează frecare?
Răspuns:
În teorie, o minge face contact punctual cu suprafața.
Dar, în realitate, mingea (și/sau suprafața) se deformează din cauza sarcinii, iar zona de contact devine eliptică.
În teorie, suprafețele de rulare, cum ar fi cele care se găsesc în majoritatea rulmenților rotativi și liniari (cu excepția lagărelor de alunecare), nu ar trebui să întâmpine forțe de frecare.
Dar în aplicațiile din lumea reală, trei factori cauzează frecare pe suprafețele de rulare:
1. Micro-alunecare între suprafețe (suprafețele alunecă una față de alta)
2. Proprietăți inelastice (adică deformare) ale materialelor
3. Rugozitatea suprafetelor
Întrebarea 4: Un obiect cu masa de 10 kg este plasat pe o suprafață netedă. Frecarea statică dintre aceste două suprafețe este dată ca 15 N. Aflați coeficientul de frecare statică?
Soluţie:
Dat
m = 10 kg
F = 15 N
ms= ?
Noi stim aia,
Forța normală, N = mg
Deci, N = 10× 9,81 = 98,1 N
Formula pentru coeficientul de frecare statică este:
ms= 15/N
algoritm de cabinăms= 15/98,1
m s = 0,153
Întrebarea 5: Forța normală și forța statică de frecare a unui obiect sunt 50 N și, respectiv, 80 N. Aflați coeficientul de frecare statică?
Soluţie:
Dat
N = 50 N
F = 80 N și μs= ?
Formula pentru coeficientul de frecare statică este
ms= F/N
ms= 80/50
ms= 1,6
Întrebarea 6: Care este relația dintre frecarea statică și cea cinetică?
Răspuns:
Forța de frecare statică menține un obiect staționar în repaus. Odată ce forța de frecare statică este depășită, forța de frecare cinetică este cea care încetinește un obiect în mișcare.
Întrebarea 7: Un frigider cântărește 1619 N și coeficientul de frecare static este de 0,50. Care este cea mai mică forță folosită pentru a muta frigiderul?
Soluţie:
Date date:
Greutatea frigiderului, W=1619 N
L=1619 N
Coeficientul de frecare statică, μs= 0,50
Forța minimă necesară pentru a muta frigiderul poate fi dată ca:
F = msÎN
F = 0,50 × 1619
F = 809,50 N.
