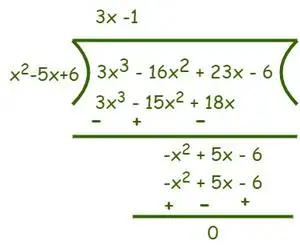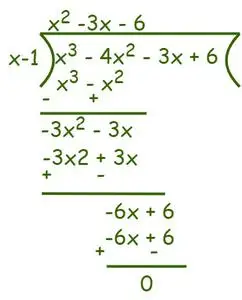Ecuația cubică este o ecuație matematică în care un polinom de gradul 3 este echivalat cu o constantă sau un alt polinom de gradul maxim 2. Reprezentarea standard a ecuației cubice este topor ³ +bx ² +cx+d = 0 unde a, b, c și d sunt numere reale. Câteva exemple de ecuație cubică sunt X ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 etc.

Cuprins

• Definiție polinom
• Gradul de ecuație
• Definiția ecuației cubice
• Cum se rezolvă ecuațiile cubice?
• Rezolvarea ecuațiilor cubice
• Rezolvarea ecuației cubice folosind factori
• Rezolvarea ecuației cubice folosind metoda grafică
• Probleme bazate pe rezolvarea ecuațiilor cubice
• Exersați probleme de rezolvare a ecuațiilor cubice

Pentru a învăța cum să rezolvăm ecuațiile cubice, trebuie mai întâi să învățăm despre polinoame, gradul polinomului și altele. În acest articol, vom afla despre, polinoame, ecuații polinomiale, rezolvarea ecuațiilor cubice sau cum să rezolvăm ecuații cubice și altele în detaliu.

Definiție polinom

Polinomul este definit după cum urmează,

A polinom este o expresie algebrică în care puterea unei variabile este un întreg nenegativ. Forma generală a unui polinom este a₀Xⁿ+ a₁X^n-1+ a₂X^n-2+… + a_n. În funcție de puterea maximă a variabilei, un polinom poate fi clasificat ca monom, binom, trinom și așa mai departe.

Ce este o ecuație?

O ecuație este definită după cum urmează,

O ecuație este un polinom care este echivalat cu o valoare numerică sau cu orice alt polinom. De exemplu, x + 2 este un polinom, dar x + 2 = 5 este o ecuație. În mod similar, 2x + 3 = x + 1 este, de asemenea, o ecuație, în timp ce 2x + 3 și x + 1 sunt polinoame individual.

Gradul de ecuație

Definiția gradului de ecuație este prezentată mai jos:

Gradul unei ecuații este definită ca puterea maximă deținută de variabila într-o ecuație.

Pe baza gradului ecuației, o ecuație poate fi clasificată după cum urmează:

• Ecuație liniară
• Ecuația pătratică
• Ecuația cubică
• Ecuație biquadratică

Ecuație liniară

Ecuația în care puterea maximă a variabilei este 1 se numește ecuație liniară.

• De exemplu 3x +1 = 0

Polinom pătratic

Ecuația în care puterea maximă a variabilei este 2 este o ecuație cuadratică.

• De exemplu 3x²+x+1 = 0

Ecuația cubică

Ecuația în care puterea maximă a variabilei este 3 se numește ecuație cubică.

• De exemplu 5x³+3x²+x+1 = 0

Polinom biquadratic

Ecuația în care puterea maximă a variabilei este 4 se numește polinom biquadratic sau polinom quartic.

• De exemplu 5x⁴+4x³+3x²+2x+1 = 0

Definiția ecuației cubice

Ecuația cubică este o ecuație algebrică în care cel mai înalt grad al polinomului este 3. Câteva exemple de ecuații cubice sunt 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 etc.

Forma generală a unei ecuații cubice este:

topor ³ + bx ² + cx + d = 0, a ≠ 0

Unde,

• a, b, și c sunt coeficienții variabilei și exponenții acestora și d este constanta și
• a, b, c și d sunt numere reale.

Cum se rezolvă ecuațiile cubice?

O ecuație cubică este o ecuație cu gradul trei. Are trei soluții și poate fi rezolvată cu ușurință urmând pașii adăugați mai jos,

Pasul 1: Găsiți o soluție a ecuației cubice prin metoda loviți și încercați. Să presupunem că avem o ecuație cubică P(x), apoi găsim pentru orice x = a, P(a) = 0 luând, x = 0, ±1, ±2, ±3, … și așadar.

Pasul 2: Când obținem, P(a) = 0, găsim factorul (x – a) al lui P(x)

Pasul 3: Împărțiți P(x) la (x – a) pentru a obține o ecuație pătratică să spunem Q(x) folosind diviziunea polinomială.

Pasul 4: Factarizați ecuația pătratică Q(x) pentru a obține factorii ca (x – b) și (x – c).

Pasul 5: (x – a), (x – b) și (x – c) sunt factorii lui P(x) și rezolvând fiecare factor obținem rădăcinile ecuației ca, a, b și c.

Află mai multe despre, Polinom împărțitor

Rezolvarea ecuațiilor cubice

A Ecuația cubică poate fi rezolvată prin două metode

• Reducându-l într-o ecuație pătratică și apoi rezolvându-l fie prin factorizare, fie prin formula pătratică
• Prin Metoda Grafică

A Ecuația cubică are trei rădăcini. Aceste rădăcini pot fi reale sau imaginare. De asemenea, pot exista rădăcini distincte sau două rădăcini identice și una diferită și toate cele trei rădăcini identice.

Trebuie remarcat faptul că pentru orice ecuație, inclusiv Ecuații cubice , ecuația trebuie întotdeauna aranjată în forma ei standard mai întâi înainte de rezolvarea ecuației.

De exemplu, dacă ecuația dată este 2x²-5 = x + 4/x, atunci trebuie să rearanjam acest lucru în forma sa standard, adică 2x³-X²-5x-4 = 0. Acum, putem rezolva ecuația folosind orice metodă adecvată.

Rezolvarea ecuației cubice folosind factori

Soluția ecuației cubice folosind teorema factorului este explicată folosind exemplul adăugat mai jos,

Exemplu: Aflați rădăcinile ecuației f(x) = 3x ³ −16x ² + 23x − 6 = 0.

Soluţie:

Expresie dată: f(x) = 3x³−16x²+ 23x − 6 = 0

Mai întâi, factorizați polinomul pentru a obține rădăcini

Deoarece constanta este -6, factorii posibili sunt 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Știm că, conform Teorema factorului dacă f(a) = 0, atunci (x-a) este un factor al lui f(x)

modele de design java

Deci, (x – 2) și (x – 3) sunt factori ai f(x). Prin urmare, produsul dintre (x – 2) și (x – 3) va fi de asemenea factor de f(x). Acum, pentru a găsi factorii rămași, utilizați metoda diviziunii lungi și împărțiți f(x) prin produsul dintre (x – 2) și (x – 3)

Prin urmare, Divizor = (x – 2)(x – 3) = (x²– 5x + 6) și Dividend = 3x³−16x²+ 23x − 6. Acum împărțiți așa cum se arată mai jos,

După împărțire obținem (3x- 1) ca cât și restul este 0. Acum conform Algoritmul de divizare noi stim aia Dividend = Divizor×Ceficient+Resier.

⇒ f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Deoarece f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 sau 3x-1 = 0

Acum vom lua 3x-1 = 0 ⇒ x = 1/3 deoarece știm deja două rădăcini din x²– 5x + 6 care sunt 2 și 3

Asa de,

Rădăcinile datei Ecuația cubică sunt 1/3, 2 și 3.

Rezolvarea ecuației cubice folosind metoda grafică

O ecuație cubică este rezolvată grafic atunci când nu puteți rezolva ecuația dată folosind alte tehnici. Deci, avem nevoie de un desen precis al ecuației cubice date. Rădăcinile ecuației sunt punctul (punctele) în care graficul traversează axa X dacă ecuația este în termenii lui x și dacă ecuația este în termenii lui y, atunci rădăcinile ecuației sunt punctele în care graficul taie axa Y.

Numărul de soluții reale ale ecuației cubice este egal cu numărul de ori în care graficul ecuației cubice traversează axa X.

Exemplu: Găsiți rădăcinile ecuației f(x) = x ³ − 4x ² − 9x + 36 = 0, folosind metoda grafică.

Soluţie:

Expresia dată: f(x) = x³− 4x²− 9x + 36 = 0.

Acum, pur și simplu înlocuiți valori aleatoare pentru x în grafic pentru funcția dată:

X	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24 gestionarea excepțiilor java	10	0	0	16

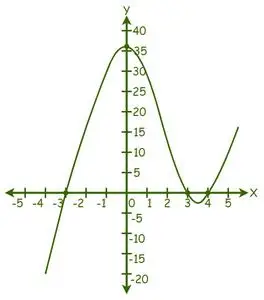
Putem vedea că graficul a tăiat axa X în 3 puncte, prin urmare, există 3 soluții reale.

Din grafic, soluțiile sunt: ​​x = -3, x = 3 și x = 4.

Prin urmare, rădăcinile ecuației date sunt -3, 3 și 4.

java obține ora curentă

Citeşte mai mult,

• Ecuație liniară
• Rezolvarea ecuației cuadratice
• Factorizarea polinoamelor

Probleme bazate pe rezolvarea ecuațiilor cubice

Problema 1: Aflați rădăcinile lui f(x) = x ³ – 4x ² -3x + 6 = 0.

Soluţie:

Expresia dată: f(x) = x³– 4x²-3x + 6 = 0.

Mai întâi, factorizați polinomul pentru a obține rădăcini.

Deoarece constanta este +6, factorii posibili sunt 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Deci, conform Teorema factorului (x – 1) este un factor al ecuației date. Acum, pentru a găsi factorii rămași, utilizați metoda diviziunii lungi.

Conform Algoritmul de divizare putem scrie,

Deci, f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 sau (x²– 3x – 6) = 0

Știm că rădăcinile unei ecuații pătratice ax²+ bx + c = 0 sunt,

x = [-b ± √(b²-4ac)]/2a

Prin urmare, pentru (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Prin urmare, rădăcinile ecuației cubice date sunt 1, (3+√33)/2 și (3–√33)/2.

Problema 2: Aflați rădăcinile ecuației f(x) = 4x ³ – 10x ² + 4x = 0.

Soluţie:

Expresie dată: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 sau 4x – 2 = 0, x – 2 = 0

⇒ x = 0 sau x = 1/2 sau x = 2

Prin urmare, rădăcinile ecuației date sunt 0, 1/2 și 2.

Problema 3: Aflați rădăcinile ecuației f(x) = x ³ + 3x ² + x + 3 = 0.

Soluţie:

Expresia dată: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 sau x²+1 = 0

⇒ x = -3, ±i

Deci, ecuația dată are o rădăcină reală, adică -3, și două rădăcini imaginare, adică ±i.

Problema 4: Aflați rădăcinile ecuației f(x) = x ³ – 7x ² – x + 7 = 0.

Soluţie:

Expresii date,

f(x) = x³– 3x²– 5x + 7 = 0

Mai întâi, factorizați ecuația, f(x): x³– 3x²– 5x + 7= 0

Poate fi factorizat în (x-7)(x+1)(x-1) = 0

După factorizarea polinomului, putem găsi rădăcinile echivalând fiecare factor cu zero. De exemplu:

• x – 7 = 0, deci x = 7
• x + 1 = 0, deci x = -1
• x – 1 = 0, deci x = 1

Deci rădăcinile ecuației f(x): x³– 3x²– 5x + 7 = 0 sunt

• x = 7
• x = -1
• x = 1

Problema 5: Aflați rădăcinile ecuației f(x) = x ³ − 6x ² + 11x − 6 = 0, folosind metoda grafică.

Soluţie:

Expresia dată: f(x) = x³− 6x²+ 11x − 6 = 0.

Acum, pur și simplu înlocuiți valori aleatoare pentru x în grafic pentru funcția dată:

X	1	2	3	4	5
f(x)	0	0	0	6	24 arp-o comandă

Putem vedea că graficul a tăiat axa X în 3 puncte, prin urmare, există 3 soluții reale.

Din grafic, soluțiile sunt: ​​x = 1, x = 2 și x = 3.

Prin urmare, rădăcinile ecuației date sunt 1, 2 și 3.

Exersați probleme de rezolvare a ecuațiilor cubice

Mai jos sunt adăugate diverse probleme practice legate de ecuațiile cubice. Rezolvați aceste probleme pentru a înțelege pe deplin conceptul Cum se rezolvă ecuația cubică?

P1. Rezolvați ecuația cubică, 3x³+ 2x²– 11x + 7 = 0.

P2. Aflați rădăcinile ecuației cubice, 4x³– 12x²+ 17 = 0.

P3. Rezolvați ecuația cubică, x³+ 4x²– x + 3 = 0 folosind metoda grafică.

P4. Găsiți numărul care satisface, -9x³+ 11x²– 8x + 2 = 0.

Întrebări frecvente despre rezolvarea ecuațiilor cubice

1. Ce sunt ecuațiile cubice?

Ecuațiile cubice sunt ecuațiile algebrice în care puterea maximă a unei variabile este 3

2. Cum se factorizează o ecuație cubică?

Putem factoriza o ecuație cubică în două moduri. Mai întâi luând o expresie liniară comună din ecuația cubică dată, apoi vom avea ca produs o expresie liniară și una pătratică. Această ecuație pătratică poate fi factorizată în continuare pentru a obține toți factorii. A doua metodă este de a găsi un zero al ecuației cubice date punând valori aleatorii. Valoarea pentru care obținem ca valoarea ecuației să fie zero va fi unul dintre zerourile ecuației cubice date. Acum, folosind teorema factorului, formează o expresie liniară, să spunem x-a și să împărțim ecuația cubică dată la această expresie, care va da o ecuație pătratică ca cât. Această ecuație pătratică obținută poate fi factorizată în continuare pentru a obține toți factorii.

3. Cum rezolvi grafic o ecuație cubică?

Pentru a rezolva grafic o ecuație cubică, puneți valori aleatoare pentru x în ecuația cubică dată și rezolvați, veți obține valorile lui y. Reprezentați pe grafic aceste valori obținute. Găsiți coordonatele la care graficul intersectează axa x. Aceste coordonate sunt soluția ecuației cubice.

4. Pot fi rezolvate exact toate ecuațiile cubice?

Orice ecuație care are o putere impară trebuie să aibă o rădăcină reală. Prin urmare, o ecuație cubică trebuie să aibă cel puțin o rădăcină reală, spre deosebire de o ecuație pătratică în care ambele rădăcini pot fi imaginare când discriminantul este mai mic decât zero.

5. Poate o ecuație cubică să aibă mai multe soluții?

Da, ecuațiile cubice pot avea mai multe soluții, deoarece o ecuație cubică poate avea până la trei rădăcini reale distincte.

6. Ce înțelegeți prin gradul unei ecuații?

Puterea maximă deținută de variabilă într-o ecuație se numește gradul unui polinom.

7. Care este diferența dintre un polinom și o ecuație?

Polinomul este pur și simplu o ecuație algebrică în care puterea variabilei este un întreg nenegativ. Acest polinom atunci când este echivalat (=) cu o valoare numerică sau un alt polinom, atunci se numește ecuație.

8. Care este teorema factorului pentru ecuațiile cubice?

Teorema factorului afirmă că dacă r este o rădăcină (soluție) a ecuației cubice ax³+ bx²+ cx + d = 0, atunci x – r este un factor al ecuației.

9. Ce se întâmplă dacă nu pot găsi soluții exacte folosind formule?

Dacă găsirea soluțiilor exacte pare imposibilă, putem folosi metode numerice precum metodele iterative (de exemplu, metoda lui Newton) pentru a aproxima rădăcinile ecuației.

Află mai multe despre Metoda lui Newton Raphson .