Condiție preliminară: Regresie liniara
Regresia liniară este un algoritm de învățare automată bazat pe învățarea supravegheată. Îndeplinește o sarcină de regresie. Regresia modelează o valoare de predicție țintă bazată pe variabile independente. Este folosit mai ales pentru a afla relația dintre variabile și prognoză. Diferite modele de regresie diferă în funcție de – tipul de relație dintre variabilele dependente și independente, pe care le iau în considerare și numărul de variabile independente utilizate. Acest articol va demonstra cum să utilizați diferitele biblioteci Python pentru a implementa regresia liniară pe un anumit set de date. Vom demonstra un model liniar binar, deoarece acesta va fi mai ușor de vizualizat. În această demonstrație, modelul va folosi Gradient Descent pentru a învăța. Puteți afla despre asta aici.
Pasul 1: Importul tuturor bibliotecilor necesare
Python3
import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn>import> preprocessing, svm> from> sklearn.model_selection>import> train_test_split> from> sklearn.linear_model>import> LinearRegression> |
>
care a făcut școala
>
Pasul 2: Citirea setului de date:
Python3
df>=> pd.read_csv(>'bottle.csv'>)> df_binary>=> df[[>'Salnty'>,>'T_degC'>]]> > # Taking only the selected two attributes from the dataset> df_binary.columns>=> [>'Sal'>,>'Temp'>]> #display the first 5 rows> df_binary.head()> |
>
>
Ieșire:
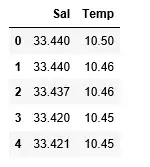
Pasul 3: Explorarea dispersării datelor
Python3
#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary, order>=> 2>, ci>=> None>)> plt.show()> |
>
>
Ieșire:

Pasul 4: Curățarea datelor
Python3
# Eliminating NaN or missing input numbers> df_binary.fillna(method>=>'ffill'>, inplace>=> True>)> |
>
>
Pasul 5: Pregătirea modelului nostru
Python3
Java comparabil
X>=> np.array(df_binary[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary[>'Temp'>]).reshape(>->1>,>1>)> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace>=> True>)> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > # Splitting the data into training and testing data> regr>=> LinearRegression()> > regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
Ieșire:

Pasul 6: Explorând rezultatele noastre
Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> # Data scatter of predicted values> |
>
>
Ieșire:

Scorul de precizie scăzut al modelului nostru sugerează că modelul nostru regresiv nu s-a potrivit foarte bine cu datele existente. Acest lucru sugerează că datele noastre nu sunt potrivite pentru regresia liniară. Dar uneori, un set de date poate accepta un regresor liniar dacă luăm în considerare doar o parte a acestuia. Să verificăm această posibilitate.
Pasul 7: Lucrul cu un set de date mai mic
Python3
df_binary500>=> df_binary[:][:>500>]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary500,> >order>=> 2>, ci>=> None>)> |
>
>
Ieșire:

Putem observa deja că primele 500 de rânduri urmează un model liniar. Continuând cu aceiași pași ca înainte.
Python3
df_binary500.fillna(method>=>'fill'>, inplace>=> True>)> > X>=> np.array(df_binary500[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary500[>'Temp'>]).reshape(>->1>,>1>)> > df_binary500.dropna(inplace>=> True>)> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > regr>=> LinearRegression()> regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
Ieșire:

Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> |
>
>
Ieșire:

Pasul 8: Măsuri de evaluare pentru regresie
În cele din urmă, verificăm performanța modelului de regresie liniară cu ajutorul unor metrici de evaluare. Pentru algoritmii de regresie folosim pe scară largă valorile mean_absolute_error și mean_squared_error pentru a verifica performanța modelului.
Python3
sistem de operare în rețea
from> sklearn.metrics>import> mean_absolute_error,mean_squared_error> > mae>=> mean_absolute_error(y_true>=>y_test,y_pred>=>y_pred)> #squared True returns MSE value, False returns RMSE value.> mse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred)>#default=True> rmse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred,squared>=>False>)> > print>(>'MAE:'>,mae)> print>(>'MSE:'>,mse)> print>(>'RMSE:'>,rmse)> |
>
>
Ieșire:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078>
