Condiție preliminară: Indicatori Introducere

Luați în considerare următorul program:

C

>

>

În programul de mai sus, avem un pointer ptr care indică 0^thelement al matricei. În mod similar, putem declara și un pointer care poate indica întregul tablou în loc de doar un element al matricei. Acest indicator este util atunci când vorbim despre tablouri multidimensionale.

Sintaxă:

data_type  (* var_name ) [size_of_array];>

Aici:

data_type este tipul de date pe care le deține matricea. var_name este numele variabilei pointer. size_of_array este dimensiunea matricei către care va indica pointerul.

Exemplu

int (*ptr)[10];>

Aici ptr este pointerul care poate indica o matrice de 10 numere întregi. Deoarece indicele au o prioritate mai mare decât indirecția, este necesar să includeți operatorul de indirectare și numele indicatorului în paranteze. Aici tipul de ptr este „pointer către o matrice de 10 numere întregi”.

Notă: indicatorul care indică 0^thelementul matricei și pointerul care indică întreaga matrice sunt total diferite. Următorul program arată asta:

C

>

>

p = 0x7fff6463e890, ptr = 0x7fff6463e890 p = 0x7fff6463e894, ptr = 0x7fff6463e8a4>

Aici, p este indicatorul spre 0^thelement al matricei arr , in timp ce ptr este un pointer care indică întregul tablou arr .

• Tipul de bază al p este int în timp ce tipul de bază al ptr este „o matrice de 5 numere întregi”.
• Știm că aritmetica pointerului este efectuată în raport cu dimensiunea de bază, deci dacă scriem ptr++, atunci pointerul ptr va fi deplasat înainte cu 20 de octeți.

Figura următoare prezintă indicatorul p și ptr. Săgeata mai întunecată indică un indicator către o matrice.

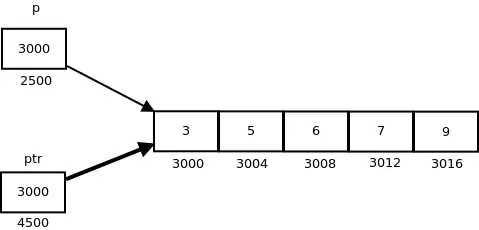
La dereferențierea unei expresii pointer obținem o valoare indicată de acea expresie pointer. Pointerul către o matrice indică o matrice, așa că, dereferențând-o, ar trebui să obținem matricea, iar numele matricei indică adresa de bază. Deci, ori de câte ori un pointer către o matrice este dereferențiat, obținem adresa de bază a matricei către care indică.

C

>

>

p = 0x7fff55adbff0, ptr = 0x7fff55adbff0 *p = 3, *ptr = 0x7fff55adbff0 sizeof(p) = 8, sizeof(*p) = 4 sizeof(ptr) = 8, sizeof(*ptr) = 20>

Pointer către tablouri multidimensionale

1. Pointeri și tablouri bidimensionale

Într-o matrice bidimensională, putem accesa fiecare element folosind două indice, unde primul indice reprezintă numărul rândului, iar al doilea indice reprezintă numărul coloanei. Elementele matricei 2-D pot fi accesate și cu ajutorul notației pointer. Să presupunem că arr este o matrice 2-D, putem accesa orice element arr[i][j] a matricei folosind expresia pointer *(*(arr + i) + j) . Acum vom vedea cum poate fi derivată această expresie.
Să luăm o matrice bidimensională arr[3][4] :

int arr[3][4] = { {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12} };>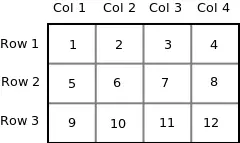

Deoarece memoria dintr-un computer este organizată liniar, nu este posibilă stocarea matricei 2-D în rânduri și coloane. Conceptul de rânduri și coloane este doar teoretic, de fapt, o matrice 2-D este stocată în ordinea principală a rândurilor, adică rândurile sunt plasate unul lângă celălalt. Următoarea figură arată cum va fi stocată în memorie matricea 2-D de mai sus.

Fiecare rând poate fi considerat ca o matrice 1-D, deci o matrice bidimensională poate fi considerată ca o colecție de matrice unidimensionale care sunt plasate una după alta. Cu alte cuvinte, putem spune că tablourile dimensionale 2D care sunt plasate una după alta. Deci aici arr este o matrice de 3 elemente în care fiecare element este o matrice 1-D de 4 numere întregi.
Știm că numele unui tablou este un pointer constant care indică 0^thMatrice 1-D și conține adresa 5000. Din moment ce arr este un „pointer către o matrice de 4 numere întregi”, conform aritmeticii pointerului, expresia arr + 1 va reprezenta adresa 5016 și expresia arr + 2 va reprezenta adresa 5032.
Deci putem spune asta arr indică 0^thmatrice 1-D, arr + 1 indică la 1^Sfmatrice 1-D și arr + 2 indică la 2^ndmatrice 1-D.

În general putem scrie:

 arr + i Points to ith element of arr ->Indică acea matrice 1-D>

• Deoarece arr + i indică spre i^thelement de arr , la dereferențiere se va obține i^thelement de arr care este desigur o matrice 1-D. Astfel expresia *(arr + i) ne oferă adresa de bază a lui i^thmatrice 1-D.
• Știm, expresia indicatorului *(arr + i) este echivalentă cu expresia indicelui arr[i] . Asa de *(arr + i) care este la fel ca arr[i] ne oferă adresa de bază a lui i^thmatrice 1-D.
• Pentru a accesa un element individual al matricei noastre 2-D, ar trebui să putem accesa orice j^thelement de i^thmatrice 1-D.
• Deoarece tipul de bază al *(arr + i) este int și conține adresa lui 0^thelement de i^thMatrice 1-D, putem obține adresele elementelor ulterioare din i^thMatrice 1-D prin adăugarea de valori întregi la *(arr + i) .
• De exemplu *(arr + i) + 1 va reprezenta adresa lui 1^Sfelement de 1^Sfelement de i^thmatrice 1-D și *(arr+i)+2 va reprezenta adresa lui 2^ndelement de i^thmatrice 1-D.
• În mod similar *(arr + i) + j va reprezenta adresa lui j^thelement de i^thmatrice 1-D. Prin dereferențierea acestei expresii putem obține j^thelementul i^thmatrice 1-D.

Pointere și tablouri tridimensionale

int arr[2][3][2] = { {{5, 10}, {6, 11}, {7, 12}}, {{20, 30}, {21, 31}, {22, 32}} };>

Într-o matrice tridimensională, putem accesa fiecare element utilizând trei indice. Să luăm o matrice 3-D - Putem considera o matrice tridimensională ca fiind o matrice de matrice 2-D, adică fiecare element al unei matrice 3-D este considerat a fi o matrice 2-D. Matricea 3-D arr poate fi considerată ca o matrice formată din două elemente în care fiecare element este o matrice 2-D. Numele matricei arr este un indicator spre 0^thmatrice 2-D.

Astfel expresia pointer *(*(*(arr + i ) + j ) + k) este echivalent cu expresia indicele arr[i][j][k].
Știm că expresia *(arr + i) este echivalentă cu arr[i] și expresia *(*(arr + i) + j) este echivalentă cu arr[i][j]. Deci putem spune că arr[i] reprezintă adresa de bază a lui i^thMatrice 2-D și arr[i][j] reprezintă adresa de bază a j^thmatrice 1-D.

Exemplu

caracteristicile java

Exemplul de mai jos demonstrează programul pentru a imprima elemente ale matricei 3D folosind pointeri.

C

>

>

5 10 6 11 7 12 20 30 21 31 22 32>

Următoarea figură arată cum este stocată în memorie matricea 3-D utilizată în programul de mai sus.

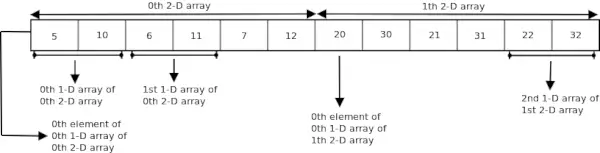
Indicator de subscriptare la o matrice

Presupune arr este o matrice 2-D cu 3 rânduri și 4 coloane și ptr este un pointer către o matrice de 4 numere întregi și ptr conține adresa de bază a matricei arr .

int arr[3][4] = {{10, 11, 12, 13}, {20, 21, 22, 23}, {30, 31, 32, 33}}; int (*ptr)[4]; ptr = arr;>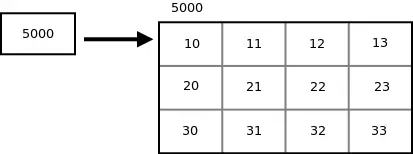

De cand ptr este un pointer către primul rând matrice 2-D, adică o matrice de 4 numere întregi, ptr + i va indica i^thrând. La dereferențiere ptr + i , obținem adresa de bază a lui i^thrând. Pentru a accesa adresa lui j^thelement de i^thrând putem adăuga j la expresia pointerului *(ptr + i) . Deci expresia pointer *(ptr + i) + j dă adresa lui j^thelement de i^thrând și expresia indicator *(*(ptr + i)+j) dă valoarea lui j^thelement de i^thrând.
Știm că expresia indicator *(*(ptr + i) + j) este echivalentă cu expresia indicele ptr[i][j]. Deci, dacă avem o variabilă pointer care conține adresa de bază a matricei 2-D, atunci putem accesa elementele matricei prin subscriptia dublă a acelei variabile pointer.

Exemplu

C

>

>

0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 0x7ffc9556b790 0x7ffc9556b7a0 0x7ffc9556b7b0 10 22 33 10 22 33>