În informatică, există unele probleme ale căror soluții nu sunt încă găsite, problemele sunt împărțite în clase cunoscute ca Clasele de complexitate . În teoria complexității, o clasă de complexitate este un set de probleme cu complexitate asociată. Aceste clase îi ajută pe oamenii de știință să grupeze probleme în funcție de cât timp și spațiu au nevoie pentru a rezolva problemele și a verifica soluțiile. Este ramura teoriei calculului care se ocupă cu resursele necesare pentru a rezolva o problemă.
cheie primară cheie compusă
Resursele comune sunt timpul și spațiul, adică cât timp ia algoritmul pentru a rezolva o problemă și utilizarea memoriei corespunzătoare.
- Complexitatea de timp a unui algoritm este folosită pentru a descrie numărul de pași necesari pentru a rezolva o problemă, dar poate fi folosită și pentru a descrie cât timp durează verificarea răspunsului.
- Complexitatea spațială a unui algoritm descrie câtă memorie este necesară pentru ca algoritmul să funcționeze.
Clasele de complexitate sunt utile în organizarea unor tipuri similare de probleme.
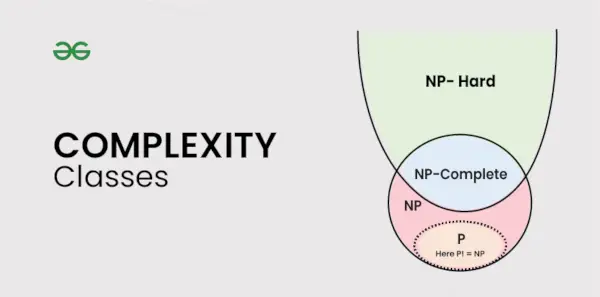
Tipuri de clase de complexitate
Acest articol discută următoarele clase de complexitate:
- Clasa P
- Clasa NP
- Clasa CoNP
- NP-greu
- NP-complet
Clasa P
P din clasa P reprezintă Timpul polinom. Este o colecție de probleme de decizie (probleme cu un răspuns da sau nu) care pot fi rezolvate de o mașină deterministă în timp polinomial.
Caracteristici:
- Soluția la P problema s este ușor de găsit.
- P este adesea o clasă de probleme de calcul care sunt rezolvabile și tratabile. Tratabil înseamnă că problemele pot fi rezolvate atât în teorie, cât și în practică. Însă problemele care pot fi rezolvate în teorie, dar nu în practică, sunt cunoscute ca insolubile.
Această clasă conține multe probleme:
- Calcularea celui mai mare divizor comun.
- Găsirea unei potriviri maxime.
- Merge Sort
Clasa NP
NP în clasa NP reprezintă Timp polinom nedeterminist . Este o colecție de probleme de decizie care pot fi rezolvate de o mașină nedeterministă în timp polinomial.
Sridevi
Caracteristici:
- Soluțiile clasei NP sunt greu de găsit, deoarece sunt rezolvate de o mașină nedeterministă, dar soluțiile sunt ușor de verificat.
- Problemele lui NP pot fi verificate de o mașină Turing în timp polinomial.
Exemplu:
Să luăm în considerare un exemplu pentru a înțelege mai bine clasa NP . Să presupunem că există o companie care are un total de 1000 angajați având un angajat unic ID-uri . Să presupunem că există 200 camere disponibile pentru ei. O selecție de 200 angajații trebuie să fie împerecheați, dar CEO-ul companiei deține datele unor angajați care nu pot lucra în aceeași cameră din motive personale.
Acesta este un exemplu de un DE EXEMPLU problemă. Deoarece este ușor să verificați dacă alegerea dată de 200 angajații propuși de un coleg este satisfăcător sau nu, adică nicio pereche luată din lista de colegi nu apare pe lista dată de CEO. Dar generarea unei astfel de liste de la zero pare să fie atât de dificilă încât să fie complet nepractică.
Indică faptul că, dacă cineva ne poate oferi soluția problemei, putem găsi perechea corectă și incorectă în timp polinomial. Astfel pentru DE EXEMPLU problema de clasă, răspunsul este posibil, care poate fi calculat în timp polinomial.
Această clasă conține multe probleme pe care cineva ar dori să le poată rezolva eficient:
- Problemă de satisfacție booleană (SAT).
- Problema traseului hamiltonian.
- Colorarea graficului.
Clasa Co-NP
Co-NP reprezintă complementul clasei NP. Înseamnă că dacă răspunsul la o problemă în Co-NP este Nu, atunci există o dovadă care poate fi verificată în timp polinomial.
Caracteristici:
- Dacă o problemă X este în NP, atunci complementul său X’ este de asemenea în CoNP.
- Pentru o problemă NP și CoNP, nu este nevoie să verificați toate răspunsurile simultan în timp polinomial, este nevoie să verificați doar un anumit răspuns da sau nu în timp polinomial pentru ca o problemă să fie în NP sau CoNP.
Câteva exemple de probleme pentru CoNP sunt:
- Pentru a verifica numărul prim.
- Factorizarea numerelor întregi.
Clasa NP-hard
O problemă NP-hard este cel puțin la fel de grea ca cea mai grea problemă din NP și este o clasă de probleme astfel încât fiecare problemă din NP se reduce la NP-hard.
Caracteristici:
- Toate problemele NP-hard nu sunt în NP.
- Este nevoie de mult timp pentru a le verifica. Aceasta înseamnă că dacă se oferă o soluție pentru o problemă NP-hard, atunci este nevoie de mult timp pentru a verifica dacă este corectă sau nu.
- O problemă A este în NP-hard dacă, pentru fiecare problemă L din NP, există o reducere în timp polinomial de la L la A.
Câteva dintre exemplele de probleme în Np-hard sunt:
șiruri de caractere java concat
- Problema opririi.
- Formule booleene calificate.
- Fără ciclu hamiltonian.
Clasa NP-complet
O problemă este NP-completă dacă este atât NP, cât și NP-hard. Problemele NP-complete sunt problemele grele din NP.
Caracteristici:
- Problemele NP-complete sunt speciale deoarece orice problemă din clasa NP poate fi transformată sau redusă în probleme NP-complete în timp polinomial.
- Dacă s-ar putea rezolva o problemă NP-completă în timp polinomial, atunci s-ar putea rezolva și orice problemă NP în timp polinomial.
Câteva exemple de probleme includ:
- Ciclul Hamiltonian.
- Satisfiabilitatea.
- Capac Vertex .
| Clasa de complexitate | Trăsătură caracteristică |
| P | Ușor rezolvabil în timp polinomial. |
| DE EXEMPLU | Da, răspunsurile pot fi verificate în timp polinomial. |
| Co-NP | Nu, răspunsurile pot fi verificate în timp polinomial. |
| NP-greu | Toate problemele NP-hard nu sunt în NP și este nevoie de mult timp pentru a le verifica. |
| NP-complet | O problemă care este NP și NP-hard este NP-completă. |
